Комбинаторика. Принцип Дирихле

Для успешной подготовки учащихся по этой теме, следует учитывать несколько факторов.
Во-первых, на изучение программирования по базовому уровню отводится незначительное количество учебного времени. За это время они должны познакомиться с языком программирования, изучить основные операторы, научиться самостоятельно записывать несложные программы с использованием трех основных типов алгоритмических конструкций (линейных, ветвления и циклических) и уметь проводить их отладку.
Во-вторых, невозможно одновременно учить комбинаторике и изучать один из языков программирования – это занимает много времени и не позволяет учащимся «видеть» задачу и пути ее решения.

Комбинаторика
один из разделов дискретной математики, который приобрёл важное значение в связи с использованием его в теории вероятностей, математической логике, теории чисел, вычислительной технике и кибернетике, а также решений заданий ЕГЭ по математике и информатике

Принцип Дирихле
Дирихле принцип (по имени П. Дирихле), принцип ящиков — предложение, утверждающее, что в случае m > n при отнесении каждого из m предметов к одному из n классов хотя бы в один класс попадёт не менее двух предметов. Это чрезвычайно простое предложение применяется при доказательстве многих важных теорем теории чисел, относящихся к приближению иррациональных чисел рациональными, в доказательствах трансцендентности чисел и других вопросах.
5 класс.
В магазин привезли 25 ящиков с яблоками 3-х сортов., причем в каждом ящике – яблоки одного сорта. Можно ли найти 9 ящиков с яблоками к-либо одного сорта?
Три купца А,Б,В и их слуги а,б,в должны на двухместной лодке переправиться через реку так, чтобы ни один из слуг не остался без хозяина в компании, где присутствует хотя бы один из остальных купцов. Возможно ли такое?
Из сосуда емкостью 8 литров надо отлить 4 л, пользуясь двумя пустыми сосудами емкостью 5 и 3 литра.

Решения 5 класс
Можно!
Т.к. сорта три, а ящиков 25, то возможны сочетания:
9+15+1, 9+14+2
9+13+3 и т.д.
Решение №2 оформляется в виде схемы

План действия
Для решения третьей задачи целесообразно записывать план действия, именно на ее примере следует вводить это понятие
8,0,0 →3,5,0→3,2,3→6,2,0→6,0,2→
1,5,2→1,4,3→4,4,0
Вариант №2: 8,0,0→5,0,3→5,3,0→
2,3,3→2,5,1→7,0,1→7,1,0→4,1,3→4,4,0

Задача Люка
Шашки расставлены в виде схемы. Требуется белые шашки поменять местами с черными, причем белые можно двигать только вправо, а черные – влево и любая шашка передвигатся либо на соседнюю пустую клетку, либо на пустую клетку, находящуюся непосредственно за ближайшей шашкой другого цвета
Решение: бччбббччччбббббчччччбббббччччбббччб

Принцип Дирихле ( 7или 8 класс)
Шестеро друзей решили в один день побывать в 7 кинотеатрах, начало сеансов в которых в 9, 10…..18,19 часов. На каждый сеанс двое шли в один кинотеатр, остальные – в другой. Доказать, что в каждом из 7 кинотеатров хотя бы на одном сеансе в этот день не был ни один из друзей.
Решение. 7-1= 6 друзей *на 11 сеансов (через каждый час по 1-му)=22 сеанса всего посетили. Если в 1-м из 7 кинотеатров они посетили все 11 сеансов, то в 6 остальных тоже посетили 11 сеансов, значит в каждом хотя бы на одном сеансе. Друзей всего 7, следовательно если брать по максимуму
На 1-м сеансе – 2 друга,
На втором – 2,
(На третьем – 2), то в сумме получаем 6, т.е. кто-то их них в этом кинотетре не был.

Множества (8-9 класс)
Определение множеств
Сложение множеств (коммуникативный и ассоциативный закон)
Пересечение множеств (дистрибутивный закон)

Комбинаторика
Задачи дискретной математики, к которым относится большинство комбинаторных задач по информатике, часто сводятся к перебору различных комбинаторных конфигураций объектов и выбору среди них наилучшего, с точки зрения условия той или иной задачи. Поэтому знание алгоритмов генерации наиболее распространенных комбинаторных конфигураций является необходимым условием успешного решения таких задач в целом. Важно также знать количество различных вариантов для каждого типа комбинаторных конфигураций, так как это позволяет реально оценить вычислительную трудоемкость выбранного алгоритма решения той или иной задачи на перебор вариантов и, соответственно, его приемлемость для решения рассматриваемой задачи, с учетом ее размерности. Кроме того, при решении задач полезным оказывается умение для каждой из комбинаторных конфигураций выполнять следующие операции: по имеющейся конфигурации получать следующую за ней в лексикографическом порядке; определять номер данной конфигурации в лексикографической нумерации всех конфигураций; и, наоборот, по порядковому номеру выписывать соответствующую ему конфигурацию.

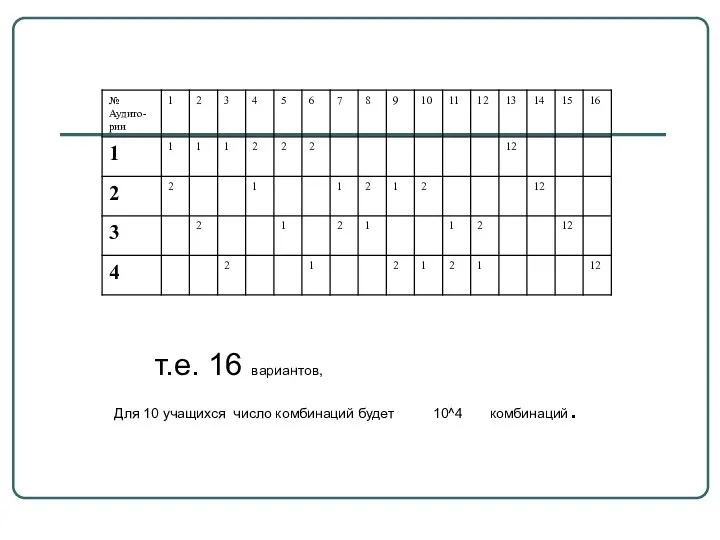
Задача 1
На олимпиаду пришло 10 учащихся из одного класса. Сколькими способами их можно разделить по четырем аудиториям, в которых они будут писать работу?

Решение 1
Для одного учащегося существует 4 способа: в 1-й аудитории, во второй, 3-й и 4-й.
Для двух учащихся – строю таблицу для наглядности

т.е. 16 вариантов,
Для 10 учащихся число комбинаций будет 10^4 комбинаций.

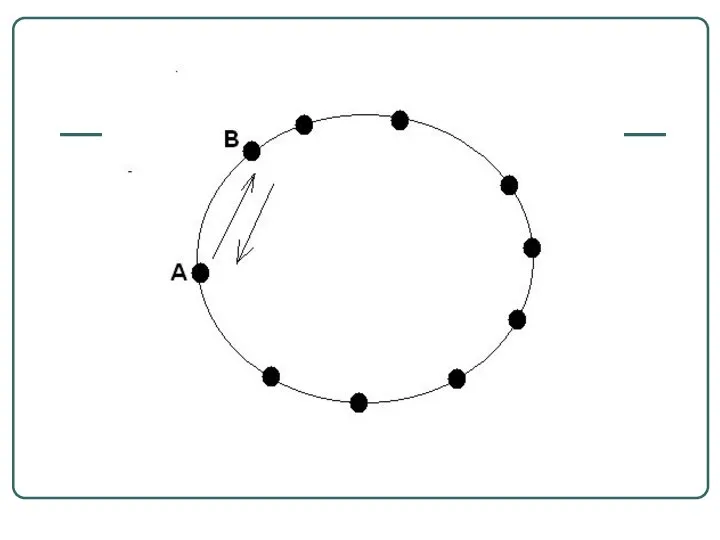
Задача 2
На окружности отмечено 10 точек. Сколько можно провести незамкнутых несамопересекающихся ломаных с вершинами во всех этих точках?

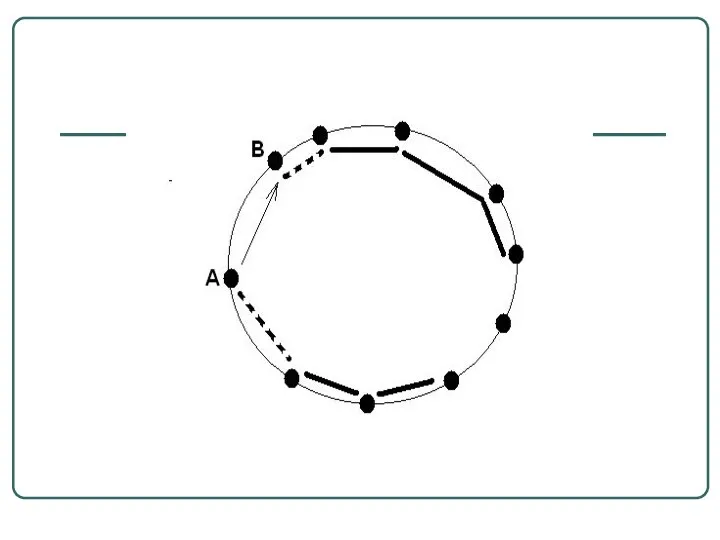
Решение 2
Возьмем произвольно точку на окружности.
Существует 2 способа начала построения первого звена ломаной.

Решение 2
После того, как первое звено проведено опять появилось две возможности и так до восьмого звена включительно:
2*2*2*2*2*2*2*2=2^8

Решение 2
При проведении девятого отрезка нет вариантов выбора (0) и есть лишь одна возможность – одна точка:
2^0=1, т.е.
2^8*2^0=2^8.
Но началом ломаной может быть любая из 10 точек: 10*2^8 вариантов.
Исключим все варианты, когда звенья строятся из А в В и из В в А (т.е. разделим на 2):

Задача. Перестановка 0, 1,2
В массиве Х (1; п) каждый элемент равен 0, 1 или 2. Переставить элементы массива так, чтобы сначала располагались все нули, затем единицы, потом двойки (дополнительного массива не заводить)

Решение.
В этой задаче при решении ничего не надо переставлять. Нужно сосчитать, сколько в массиве нулей, единиц и двоек и заполнить массив требуемым образом.

Решение.
10 INPUT n: DIM X(n)
20 FOR i = 1 TO n: INPUT X(i): NEXT
30 a1 = 0: a2 = 0
40 FOR i = 1 TO n
50 IF X(i) = 2 THEN a2 = a2 + 1 ELSE a1 = a1 + X(i)
60 NEXT i
70 a0 = n - a1 - a2: a1 = a0 + a1
80 FOR i = 1 TO n
90 IF i <= a0 THEN X(i) = 0 ELSE IF i <= a1 THEN X(i) = 1 ELSE
X(i) = 2
100 NEXT i
110 FOR i = 1 TO n: PRINT X(i): NEXT
120 END

Задача. Рюкзак.
Из заданных п предметов выбрать такие, суммарный вес которых был менее 30 кг, а стоимость наибольшей. Напечатать суммарную стоимость выбранных предметов. Точнее – заданы два массива положительных чисел А(1;п) и В(1;п). Выбрать такие попарно различные числа i, чтобы сумма i-х элементов массива А была<30, а сумма i-х элементов массива В бала наибольшей. Напечатать только величину max.

Решение
1. Исключим все предметы которые весят > 30 кг.
2. Предметы с массой менее 30 кг расположим в каком-либо порядке (возрастания, убывания).
3. Зададим три массива А(п), В(п), С(п): А(п), В(п) – по условию, С(п) – вспомогательный.
4. Обозначим: п-число предметов,
М-масса предметов в рюкзаке,
S-суммарная стоимость предметов
X-максимальная стоимость рассмотренных вариантов
i- номер предмета.
Если предмет взят: С(к)=0, если предмет к<=i не взят С(к)=1.
Вначале обнулим М, S, Х,i и ограничим число предметов t=30.
Нам надо рассмотреть все или максимально возможное число вариантов и сразу отсекать неподходящие (т.е. прекратить перебор)

Решение.
При движении вперед мы добавляем предмет в рюкзак (ЕСЛИ m + A(i)<30). В этом случае m = m + A(i) : s=s+B(i) : C(i)=0
ИЛИ не добавляем – если он нам не подходит С(i)=0 (строка №90) В обоих случаях двигаемся вперед, пока не рассмотрим последний предмет.
После того как все предметы рассмотрены, получен вариант, который сравнивается с Х: IF x < s THEN x = s и начинается движение назад:
-пропускается вся группа идущих подряд взятых предметов (у них С(i)=0 – взяты), т.к. эти группы поменять, то их суммарная стоимость только снизится
-заодно удаляем просмотренные предметы из рюкзака
IF C(i + 1) = 0 THEN m = m - A(i + 1): s = s - B(i + 1)
-затем пропускаем всю группу не взятых ранее предметов С(i)=1 чтобы не делать два раза одно и тоже.
Мы движемся назад до достижения такого номера предмета i, что C(i ) = 0 и C(i + 1) = 0 . При этом удаляем имеющиеся там предметы.
После этого движемся вперед (GOTO 80 )
Если нужного номера предмета не окажется, то GOTO END