Конструирование алгоритмов. Основы алгоритмизации

Ключевые слова
последовательное построение алгоритма
вспомогательный алгоритм
формальные параметры
фактические параметры
рекурсивный алгоритм

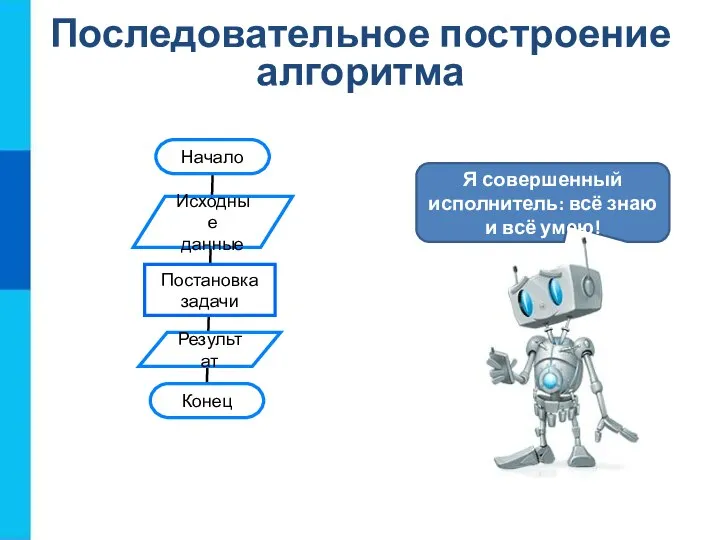
Последовательное построение алгоритма
Я совершенный исполнитель: всё знаю и всё умею!

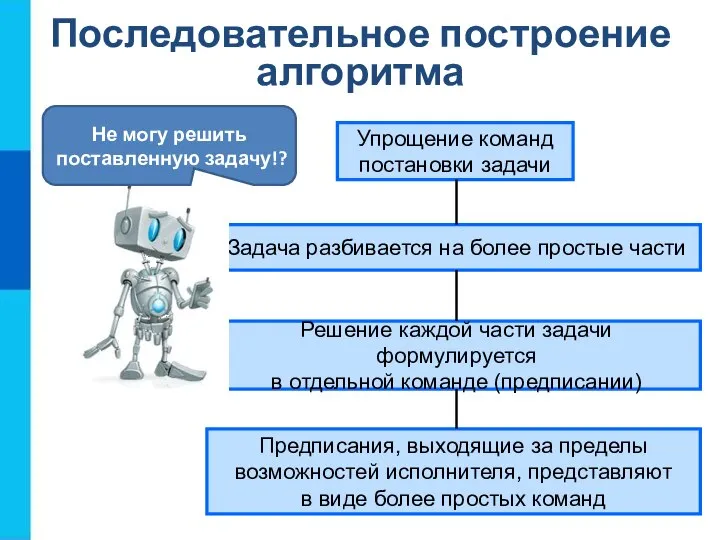
Последовательное построение алгоритма
Упрощение команд
постановки задачи
Задача разбивается на более простые части
Решение каждой части задачи формулируется
в отдельной команде (предписании)
Предписания, выходящие за пределы
возможностей исполнителя, представляют
в виде более простых команд
Не могу решить поставленную задачу!?

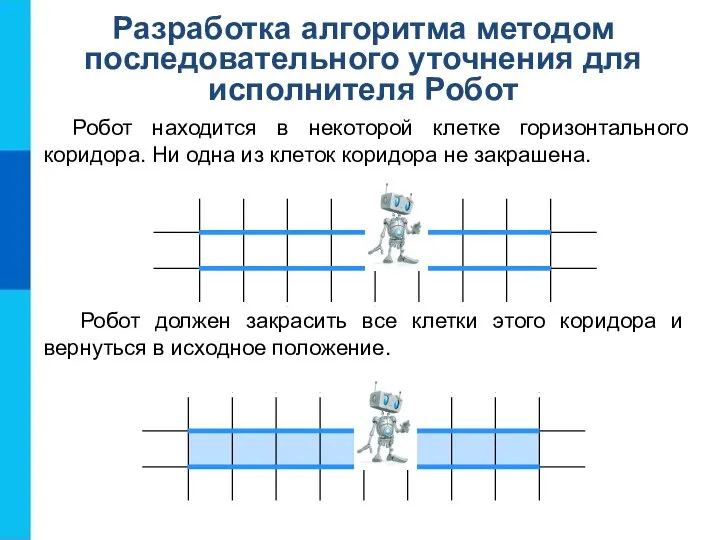
Разработка алгоритма методом последовательного уточнения для исполнителя Робот
Робот находится в некоторой клетке горизонтального коридора. Ни одна из клеток коридора не закрашена.
Робот должен закрасить все клетки этого коридора и вернуться в исходное положение.

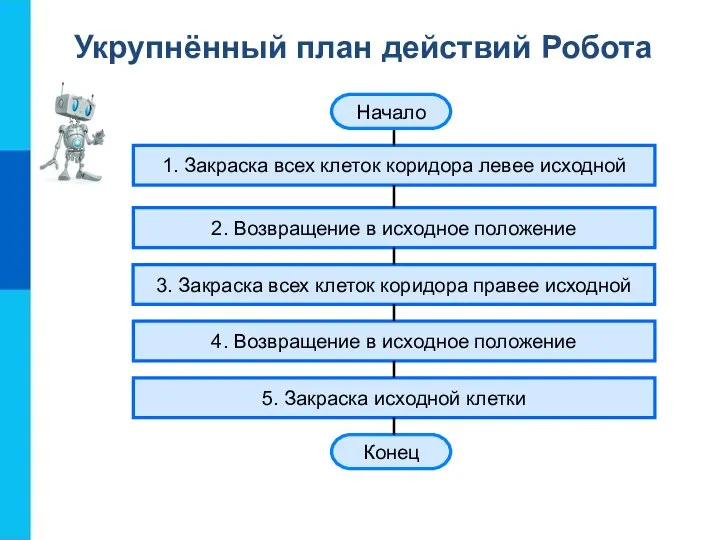
Укрупнённый план действий Робота
1. Закраска всех клеток коридора левее исходной
2. Возвращение в исходное положение
3. Закраска всех клеток коридора правее исходной
4. Возвращение в исходное положение
5. Закраска исходной клетки
Начало
Конец

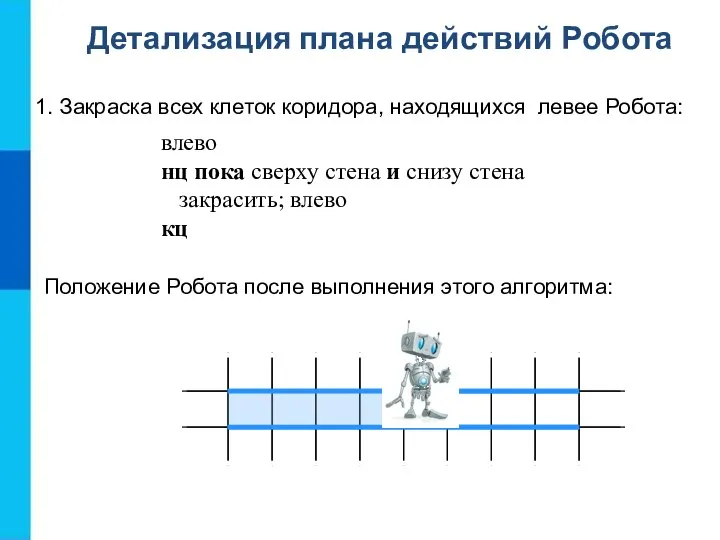
1. Закраска всех клеток коридора, находящихся левее Робота:
Детализация плана действий Робота
влево
нц пока сверху стена и снизу стена
закрасить; влево
кц
Положение Робота после выполнения этого алгоритма:

2. Возвращение Робота в коридор в исходную точку:
вправо
нц пока клетка закрашена вправо
кц
Детализация плана действий Робота
Положение Робота после выполнения этого алгоритма:

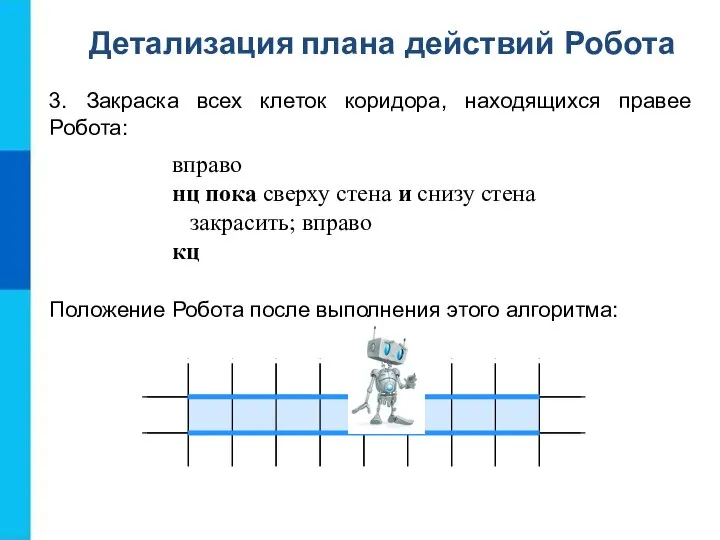
3. Закраска всех клеток коридора, находящихся правее Робота:
вправо
нц пока сверху стена и снизу стена
закрасить; вправо
кц
Детализация плана действий Робота
Положение Робота после выполнения этого алгоритма:

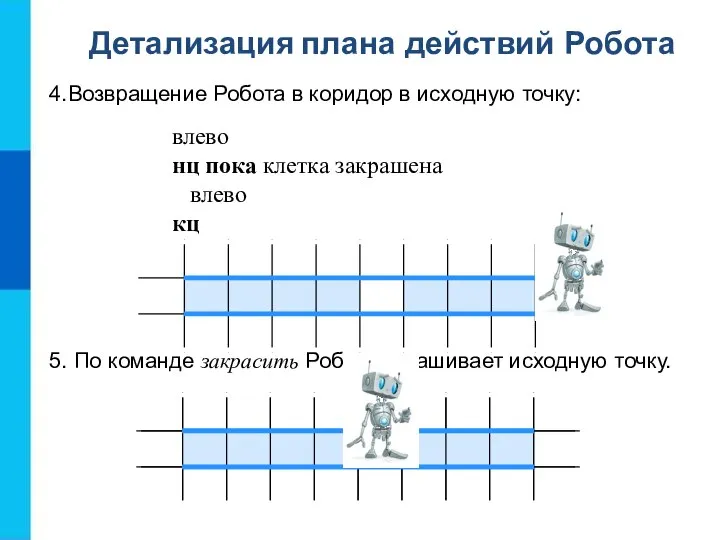
4.Возвращение Робота в коридор в исходную точку:
влево
нц пока клетка закрашена
влево
кц
5. По команде закрасить Робот закрашивает исходную точку.
Детализация плана действий Робота

алг
нач
влево
нц пока сверху стена и снизу стена
закрасить; влево
кц вправо
нц пока клетка закрашена
вправо
кц
вправо
нц пока сверху стена и снизу стена
закрасить; вправо
кц
влево
нц пока клетка закрашена
влево
кц
закрасить
кон
Программа для Робота

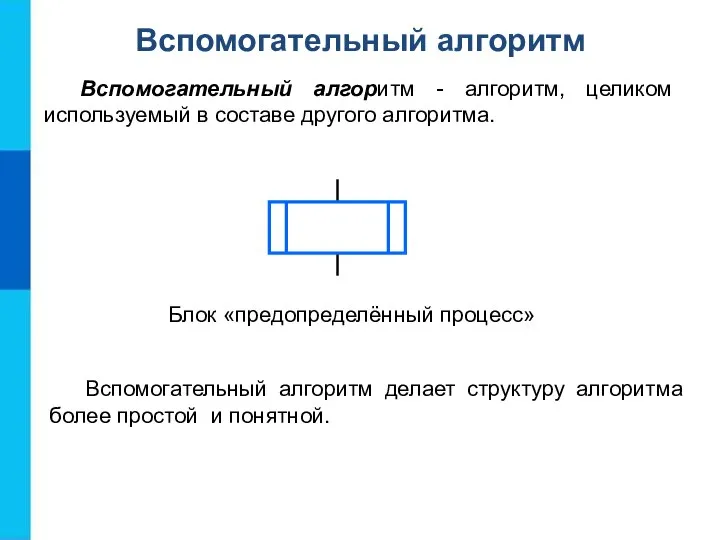
Вспомогательный алгоритм
Вспомогательный алгоритм - алгоритм, целиком используемый в составе другого алгоритма.
Блок «предопределённый процесс»
Вспомогательный алгоритм делает структуру алгоритма более простой и понятной.

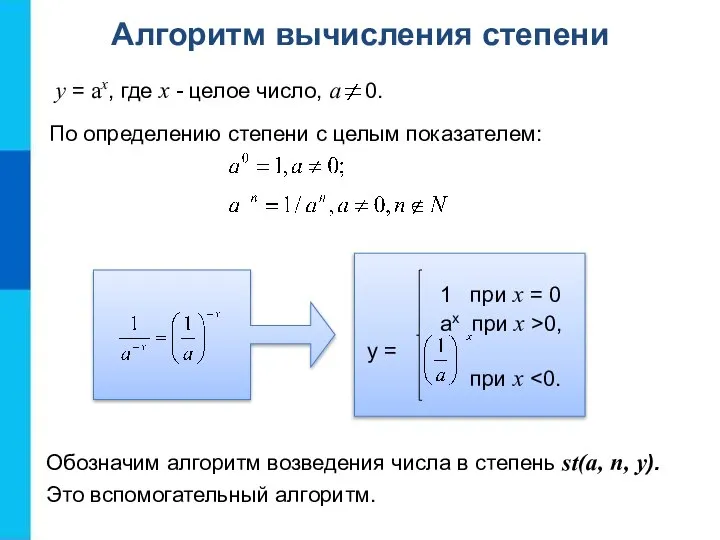
Алгоритм вычисления степени
y = ax, где x - целое число, a 0.
1 при x = 0
ax при x >0,
y =
при x <0.
Обозначим алгоритм возведения числа в степень st(a, n, y).
Это вспомогательный алгоритм.
По определению степени с целым показателем:

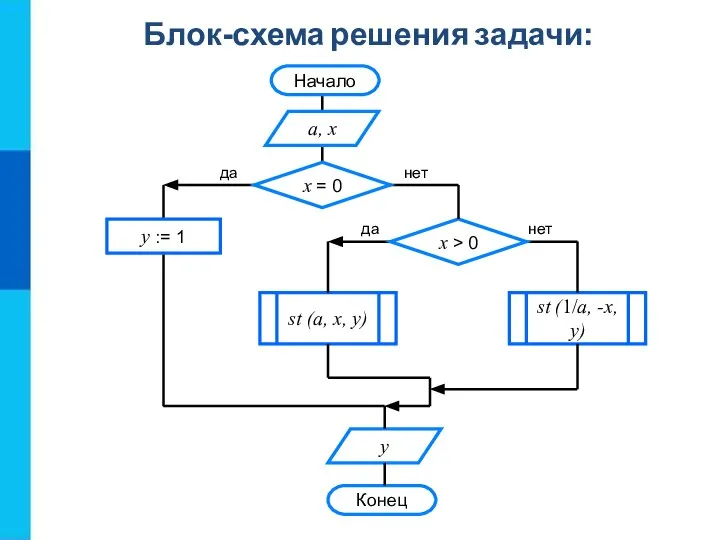
Блок-схема решения задачи:

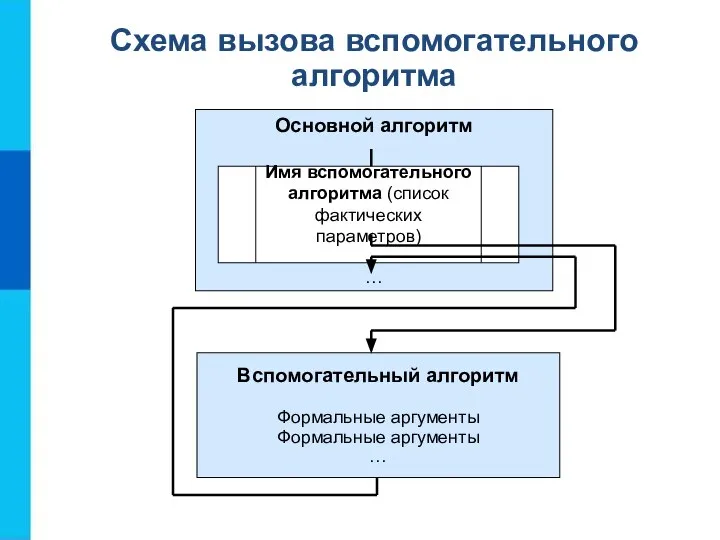
Формальные параметры используются при описании алгоритма.
Фактические параметры - те величины, для которых будет исполнен вспомогательный алгоритм.
Типы, количество и порядок следования формальных и фактических параметров должны совпадать.
Формальные и фактические параметры

Схема вызова вспомогательного алгоритма

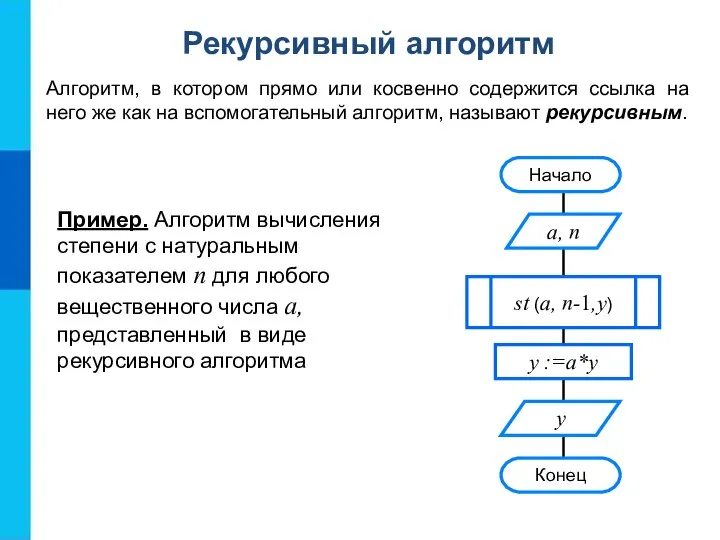
Пример. Алгоритм вычисления степени с натуральным показателем n для любого вещественного числа а, представленный в виде рекурсивного алгоритма
Рекурсивный алгоритм
Алгоритм, в котором прямо или косвенно содержится ссылка на него же как на вспомогательный алгоритм, называют рекурсивным.

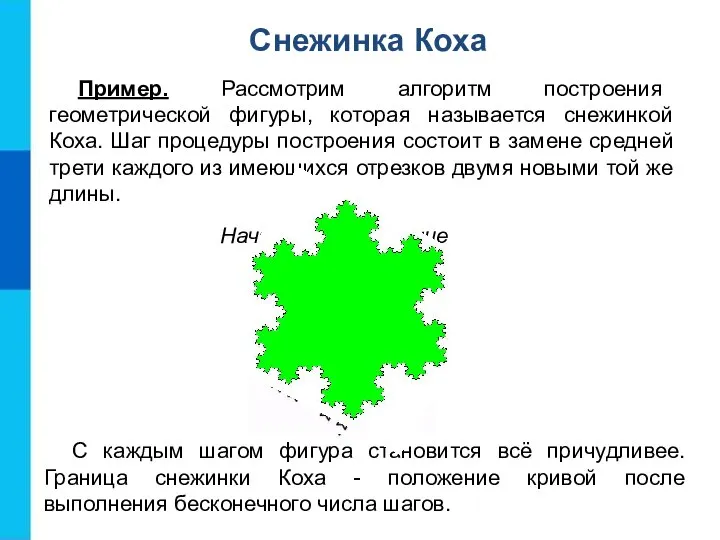
Снежинка Коха
Пример. Рассмотрим алгоритм построения геометрической фигуры, которая называется снежинкой Коха. Шаг процедуры построения состоит в замене средней трети каждого из имеющихся отрезков двумя новыми той же длины.
С каждым шагом фигура становится всё причудливее. Граница снежинки Коха - положение кривой после выполнения бесконечного числа шагов.
Начальное положение
Первый шаг
Второй шаг
Третий шаг

Самое главное
Метод последовательного построения алгоритма:
исходная задача разбивается на несколько частей, каждая из которых проще всей задачи, и решение каждой части формулируется в отдельной команде;
если получаются команды, выходящие за пределы возможностей исполнителя, то они представляются в виде совокупности ещё более простых предписаний;
процесс продолжается до тех пор, пока все предписания не будут понятны исполнителю.
Вспомогательный алгоритм - алгоритм, целиком используемый в составе другого алгоритма.
Алгоритм, в котором прямо или косвенно содержится ссылка на него же как на вспомогательный алгоритм, называют рекурсивным.

Вопросы и задания
Почему при решении сложной задачи затруднительно
сразу конкретизировать все необходимые действия?
В чём заключается метод последовательного уточнения при построении алгоритма?
Какая связь между методом последовательного построения алгоритма и такими процессами, как написание сочинения или подготовка к многодневному туристическому походу?
Известен рост каждого из N учеников 9А класса и М учеников 9Б класса.
Опишите укрупнёнными блоками алгоритм сравнения среднего роста учеников этих классов.
В ряду из десяти клеток правее Робота некоторые клетки закрашены. Последняя закрашенная клетка может примыкать к стене.
Составьте алгоритм, который закрашивает клетки выше и ниже каждой закрашенной клетки.
Проверьте работу алгоритма в следующих случаях:
Для чего нужны вспомогательные алгоритмы?
Опишите процесс выполнения команды вызова вспомогательного алгоритма в основном алгоритме.
Сталкивались ли вы с идеей формальных и фактических параметров при изучении математики и физики?
Приведите пример.
Какие алгоритмы называют рекурсивными?
Приведите пример рекурсии из жизни.
Составьте алгоритмы, под управлением которых Робот закрасит указанные клетки.
а
б
в