Слайд 2Архитектура фон Неймана
Первые компьютерные системы имели заданный набор программ
Изменение встроенной программы требовало

практически полной их переделки, что требовало огромного объёма ручной работы по подготовке новой документации, перекоммутации и перестройки блоков и устройств и т. п.
Слайд 3Архитектура фон Неймана
В 1946 г. Был предложен принцип совместного хранения программ и
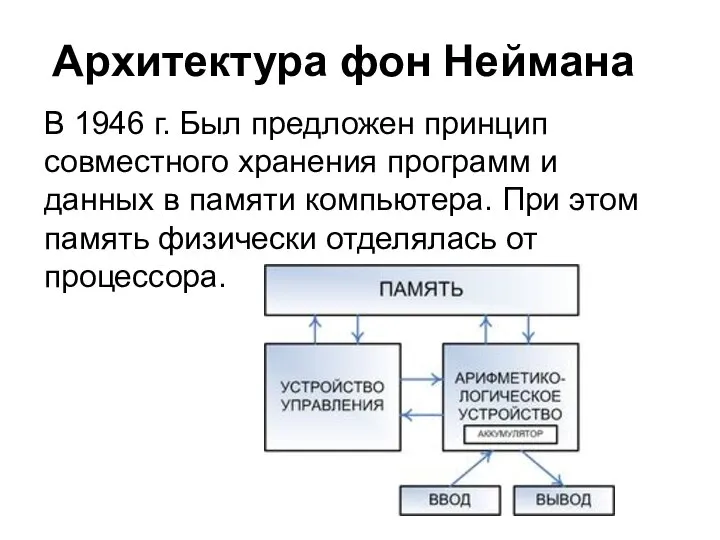
данных в памяти компьютера. При этом память физически отделялась от процессора.
Слайд 4Архитектура фон Неймана
Принципы фон Неймана:
Принцип двоичного кодирования.
Принцип однородности памяти.
Принцип адресуемости

памяти.
Принцип последовательного программного управления.
Принцип жесткости архитектуры
Слайд 5Архитектура фон Неймана
Принцип двоичного кодирования.
Для представления данных и команд используется двоичная система

счисления.
Этим обеспечивалась простота технической реализации, простота выполнения арифметических и логических операций
Слайд 6Архитектура фон Неймана
Принцип однородности памяти.
Программы и данные хранятся в одной и той

же памяти. Над командами можно выполнять такие же действия, как и над данными.
Это позволяет легко изменять программы для ЭВМ.
Слайд 7Архитектура фон Неймана
Принцип адресуемости памяти.
Структурно основная память состоит из пронумерованных ячеек, процессору

в произвольный момент времени доступна любая ячейка.
Слайд 8Архитектура фон Неймана
Принцип последовательного программного управления.
Все команды располагаются в памяти и выполняются

последовательно, одна после завершения другой, в последовательности, определяемой программой.
В зависимости от результатов работы предыдущей команды линейность может нарушаться (команды условного перехода).
Слайд 9Архитектура фон Неймана
Принцип последовательного программного управления.
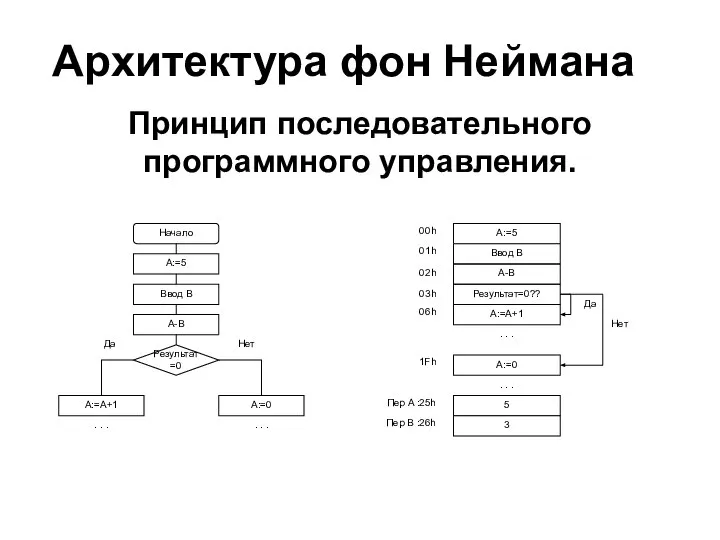
Слайд 10Архитектура фон Неймана
Принцип жесткости архитектуры
Неизменяемость в процессе работы топологии, архитектуры, списка команд.
Позволяет

повторное использование программ, использование одних и тех же программ на разных ЭВМ.
Слайд 11Системы счисления
Десятичная – наиболее удобна для понимания человеком.
Двоичная – наиболее просто реализуется

в ЭВМ.
Восьмеричная – удобна, если используются числа, имеющие количество двоичных разрядов, кратное трем.
Шестнадцатиричная – кратное четырем.
Слайд 12Системы счисления
Пример:
Права на файл в ОС UNIX
1-й бит – чтение
2-й бит –

запись
3-й бит – выполнение
7(111) – все права
5(101) – чтение и выполнение
4(100) – чтение
0(000) – нет прав
Слайд 13Системы счисления
Пример:
Адреса памяти в ОС Windows
10010010011110001111000011101010 (2)
9278F0EA (16)
2457399530 (10)

Слайд 14Представление данных
Целые беззнаковые типы
Все разряды ячейки отводятся для представления числа
1 байт=8 бит

– 0..255
2 байта=16 бит – 0..65535
4 байта=32 бита – 0.. 4294967295
300 - 00000001 00101100
1000000 - 00000000 00001111 01000010 01000000
Слайд 15Представление данных
Целые со знаком
Прямой код числа. Старший (левый) бит отводится под знак.
1

байт – -127..127
2 байта – -32767.. 32767
4 байта – -2147483647.. 2147483647
-3 10000011
+3 00000011
Слайд 16Представление данных
Прямой код в ЭВМ не используется из-за громоздкости операции сложения/вычитания
10011111 01000101
+

===? -
01000101 00011111
Слайд 17Представление данных
Целые со знаком
Дополнительный код.
1 байт – -128..127
2 байта – -32768.. 32767
4

байта – -2147483648.. 2147483647
Слайд 18Представление данных
Целые со знаком
Алгоритм преобразования в дополнительный код.
Положительное число. Записывается так же,

как в прямом коде.
00000101
00000011
128 0000000010000000
Слайд 19Представление данных
Целые со знаком
Алгоритм преобразования в дополнительный код.
Отрицательное число.
Записывается по модулю в

прямом коде.
Все биты инвертируются – нули заменяются единицами и наоборот.
К полученному прибавляется 1
Слайд 20Представление данных
Целые со знаком
Алгоритм преобразования в дополнительный код.
Примеры:
-35 1) 00100011
2) 11011100
3) 11011101

Слайд 21Представление данных
Целые со знаком
Алгоритм преобразования в дополнительный код.
Примеры:
-127 1) 01111111
2) 10000000
3) 10000001

Слайд 22Представление данных
Целые со знаком
Алгоритм преобразования в дополнительный код.
Примеры:
-128 1) 10000000
2) 01111111
3) 10000000

Слайд 23Представление данных
Целые со знаком
Алгоритм преобразования в дополнительный код.
Примеры:
-1 1) 00000001
2) 11111110
3) 11111111

Слайд 24Представление данных
Целые со знаком
Сложение чисел в дополнительном коде.
35+(-1) 00100011
+
11111111
00100010

Слайд 25Представление данных
Целые со знаком
Сложение чисел в дополнительном коде.
-35+(-35) 11011101
+
11011101
10111010 (-70 в доп. коде)

Слайд 26Представление данных
Целые со знаком
Перенос и переполнение
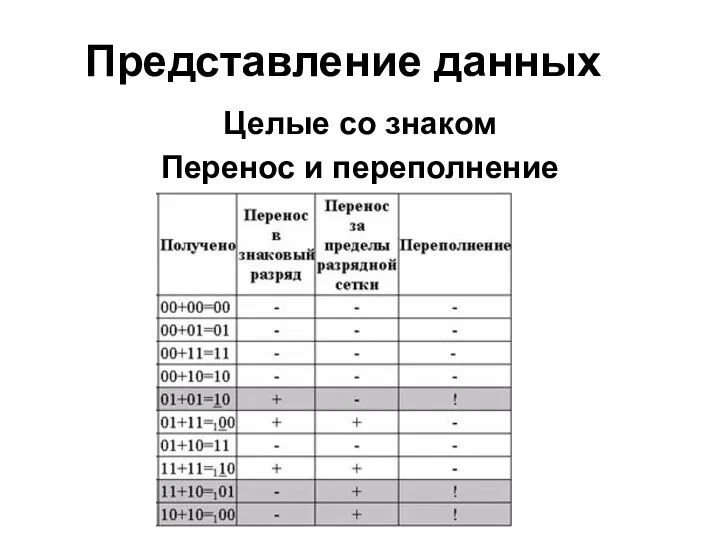
Слайд 27Представление данных
Целые со знаком
Сложение чисел в дополнительном коде.
127+1 01111111
+
00000001
10000000 (переполнение)



























 Сервер DropBox
Сервер DropBox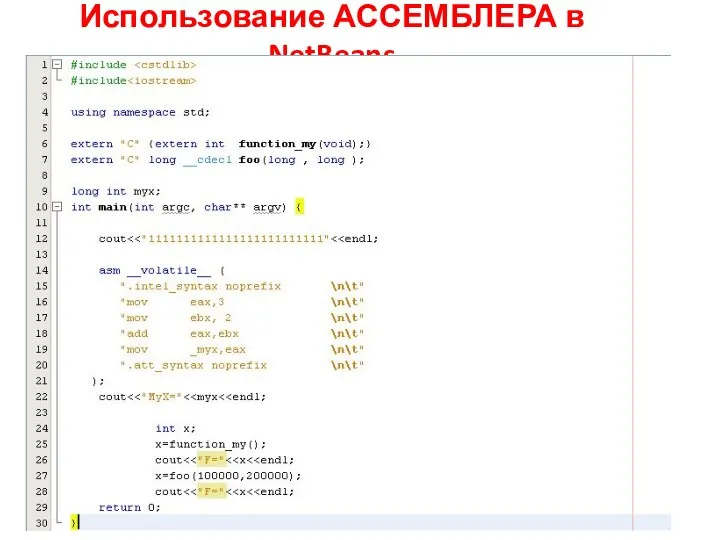 Использование ассемблера в NetBeans
Использование ассемблера в NetBeans Телекомунікації. Системи телекомунікації за типом топології та основні критерії для їх оцінки
Телекомунікації. Системи телекомунікації за типом топології та основні критерії для їх оцінки Стимулирование развития инноваций
Стимулирование развития инноваций Choose a random element from a nonempty sequence
Choose a random element from a nonempty sequence Электронные (динамические) таблицы
Электронные (динамические) таблицы Ардуино
Ардуино Восьмеричная система счисления
Восьмеричная система счисления Модульно-рейтинговая технология
Модульно-рейтинговая технология Электронная система расписания
Электронная система расписания ,ІІС, що засновані на штучних нейронних мережах лекція № 5-1
,ІІС, що засновані на штучних нейронних мережах лекція № 5-1 Система управления базами данных (СУБД)
Система управления базами данных (СУБД) Компьютер – универсальная машина для работы с информацией
Компьютер – универсальная машина для работы с информацией Преобразование информации, представленной в виде карты
Преобразование информации, представленной в виде карты Индустрия встреч как сегмент мировой ивент индустрии
Индустрия встреч как сегмент мировой ивент индустрии Гуру обработки
Гуру обработки Объектная модель Excel
Объектная модель Excel Конкурентный анализ
Конкурентный анализ Основы телекоммуникаций сетей. Технологии телекоммуникационных сети TCP/IP
Основы телекоммуникаций сетей. Технологии телекоммуникационных сети TCP/IP Зарплатные программы КАМИН для бизнеса
Зарплатные программы КАМИН для бизнеса Трехмерный анализ данных
Трехмерный анализ данных Исследование звукосимволизма с помощью Word Embedding
Исследование звукосимволизма с помощью Word Embedding 12. Арифметика в дв.СС
12. Арифметика в дв.СС Нахождение логического выражения по таблице истинности
Нахождение логического выражения по таблице истинности Python 3 middle
Python 3 middle Прямая трансляция
Прямая трансляция Экранизации игр
Экранизации игр Понятие дерева целей
Понятие дерева целей