- Главная
- Информатика
- Криптографические протоколы

Содержание
- 3. Задача византийских генералов Задача византийских генералов — в криптологии задача взаимодействия нескольких удаленных абонентов, которые получили
- 4. «синих» генералов возглавляют армии в горах и готовятся атаковать «зелёных» в долине. Для связи атакующие используют
- 5. Каждый из лояльных генералов должен получить вектор длины n, в котором i-й элемент либо обязательно содержит
- 6. Алгоритм Лесли Лампорта Рекурсивный алгоритм был предложен в 1982 г. Лесли Лампортом. Алгоритм сводит задачу для
- 7. Алгоритм Лесли Лампорта 3-й шаг. Каждый посылает свой вектор всем остальным (генерал 3 посылает опять произвольные
- 8. Алгоритм Лесли Лампорта 4-й шаг. Каждый генерал определяет для себя размер каждой армии. Чтобы определить размер
- 9. Запустить программу и изучить протокол византийского соглашения
- 10. Византийские генералы Общая картина: – Пусть вокруг города расположено n византийских отрядов, каждым командует свой генерал
- 11. Фаза 1 Генералы делятся своими наблюдениями Фаза 2 Генералы принимают решение Требования к первой фазе: 1А
- 12. Все честные генералы получат одинаковую сводку Наблюдения всех честных генералов будут поняты правильно Генералы смогут принять
- 13. ЗАДАЧА О ВИЗАНТИИСКИХ ГЕНЕРАЛАХ Командир должен передать свой приказ n — 1 лейтинанту так, чтобы были
- 14. Кстати, а почему генералы — византийские?
- 15. Но Лейтенант 2 (из симметрии) будет отступать! Противоречие с согласованностью.
- 19. Протокол византийского соглашения Протокол решения данной задачи называется протоколом византийского соглашения (byzantine agreement.) При византийских соглашениях
- 20. Схема «Византийского соглашения» с использованием квантовых коммуникаций Схема «Византийского соглашения» с использованием квантовых коммуникаций была предложена
- 21. Предложен квантовый метод обнаружения «лжецов» http://rnns.ru/5175-predlozhen-kvantovyjj-metod.html
- 22. В 1985-1986 гг., понимание различных протоколов и способов их построения привело к появлению двух значимых математических
- 24. Скачать презентацию
Слайд 3Задача византийских генералов
Задача византийских генералов — в криптологии задача взаимодействия нескольких удаленных
Задача византийских генералов
Задача византийских генералов — в криптологии задача взаимодействия нескольких удаленных

Формулировка
Византия. В ночь перед великим сражением, Византийская армия содержит легионов. Каждый из них подчиняется своему генералу. У всей византийской армии есть главнокомандующий, руководящий генералами. Империя находится в упадке и среди генералов, включая главнокомандующего, могут быть предатели. В течение всей ночи, каждый из генералов получает от предводителя приказ о действии на утро. Это может быть один из двух вариантов «атаковать» или «отступать». Если все честные генералы атакуют — они одержат победу. Если все отступят — им удастся сохранить армию. Если часть атакуют, а часть отступят — они терпят поражение. Если главнокомандующий предатель, он может дать разным генералам разные приказы, следовательно, его приказы не стоит выполнять беспрекословно. Если же каждый генерал будет действовать независимо от других, результаты битвы также могут быть плачевными. Поэтому генералы нуждаются в обмене информацией друг с другом, чтобы прийти к соглашению.
Слайд 4«синих» генералов возглавляют армии в горах и готовятся атаковать «зелёных» в долине.
«синих» генералов возглавляют армии в горах и готовятся атаковать «зелёных» в долине.

Слайд 5Каждый из лояльных генералов должен получить вектор длины n, в котором i-й
Каждый из лояльных генералов должен получить вектор длины n, в котором i-й

Слайд 6Алгоритм Лесли Лампорта
Рекурсивный алгоритм был предложен в 1982 г. Лесли Лампортом. Алгоритм сводит
Алгоритм Лесли Лампорта
Рекурсивный алгоритм был предложен в 1982 г. Лесли Лампортом. Алгоритм сводит

Для случая m=0 алгоритм тривиален, поэтому проиллюстрируем его для случая n=4 и m=1 . В этом случае алгоритм осуществляется в 4 шага.
1-й шаг. Каждый генерал посылает всем остальным сообщение, в котором указывает численность своей армии. Лояльные генералы указывают истинное количество, а предатели могут указывать различные числа в разных сообщениях. Генерал 1 указал число 1 (одна тысяча воинов), генерал 2 указал число 2, генерал 3 (предатель) указал трём остальным генералам соответственно x ,y ,z , а генерал 4 указал 4.
2-й шаг. Каждый формирует свой вектор из имеющейся информации.
Получается:
Вектор 1 (1,2,x,4);
Вектор 2 (1,2,y,4);
Вектор 3 (1,2,3,4);
Вектор 4 (1,2,z,4).
Слайд 7Алгоритм Лесли Лампорта
3-й шаг. Каждый посылает свой вектор всем остальным (генерал 3
Алгоритм Лесли Лампорта
3-й шаг. Каждый посылает свой вектор всем остальным (генерал 3
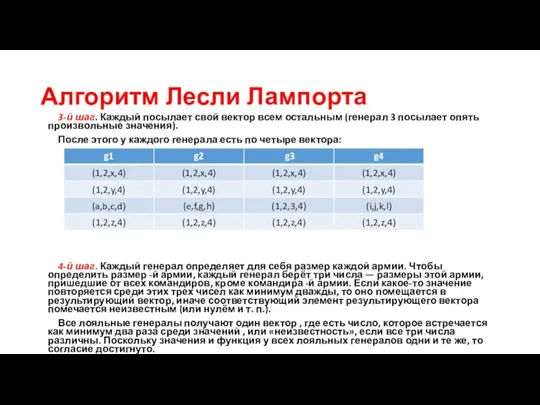
После этого у каждого генерала есть по четыре вектора:
4-й шаг. Каждый генерал определяет для себя размер каждой армии. Чтобы определить размер -й армии, каждый генерал берёт три числа — размеры этой армии, пришедшие от всех командиров, кроме командира -й армии. Если какое-то значение повторяется среди этих трех чисел как минимум дважды, то оно помещается в результирующий вектор, иначе соответствующий элемент результирующего вектора помечается неизвестным (или нулём и т. п.).
Все лояльные генералы получают один вектор , где есть число, которое встречается как минимум два раза среди значений , или «неизвестность», если все три числа различны. Поскольку значения и функция у всех лояльных генералов одни и те же, то согласие достигнуто.
Слайд 8Алгоритм Лесли Лампорта
4-й шаг. Каждый генерал определяет для себя размер каждой армии.
Алгоритм Лесли Лампорта
4-й шаг. Каждый генерал определяет для себя размер каждой армии.

Все лояльные генералы получают один вектор (1,2,f(x,y,z),4) , где f(x,y,z) есть число, которое встречается как минимум два раза среди значений (x,y,z) , или «неизвестность», если все три числа (x,y,z) различны. Поскольку значения x,y,z и функция f у всех лояльных генералов одни и те же, то согласие достигнуто.
Слайд 9Запустить программу и изучить протокол византийского соглашения
Запустить программу и изучить протокол византийского соглашения

Слайд 10Византийские генералы
Общая картина:
– Пусть вокруг города расположено n византийских отрядов, каждым командует
Византийские генералы
Общая картина:
– Пусть вокруг города расположено n византийских отрядов, каждым командует

– У каждого генерала есть некоторая информация
– Генералы могут посылать сообщения другим генералам
Среди генералов могут быть предатели
Требования:
А Все честные генералы принимают одинаковое решение
Б Малое количество предателей не способно заставить честных выбрать "плохой план"
Слайд 11Фаза 1 Генералы делятся своими наблюдениями
Фаза 2 Генералы принимают решение
Требования к
Фаза 1 Генералы делятся своими наблюдениями
Фаза 2 Генералы принимают решение
Требования к

1А Наблюдения честных генералов до других честных генералов дойдут неискаженными
1Б От нечестного генерала все честные генералы получат одинаковое наблюдение
Анализ плана:
Все честные генералы получат одинаковую сводку
Фаза 1 Генералы делятся своими наблюдениями
Фаза 2 Генералы принимают решение
План протокола
Слайд 12Все честные генералы получат одинаковую сводку
Наблюдения всех честных генералов будут поняты
Все честные генералы получат одинаковую сводку
Наблюдения всех честных генералов будут поняты

Слайд 13ЗАДАЧА О ВИЗАНТИИСКИХ ГЕНЕРАЛАХ
Командир должен передать свой приказ n — 1 лейтинанту
ЗАДАЧА О ВИЗАНТИИСКИХ ГЕНЕРАЛАХ
Командир должен передать свой приказ n — 1 лейтинанту

Согласованность Все генералы получат одинаковый приказ
Исполнительность Если командир честен, то приказ будет совпадать с исходным
Слайд 14Кстати, а почему генералы — византийские?
Кстати, а почему генералы — византийские?

Слайд 15Но Лейтенант 2 (из симметрии) будет отступать! Противоречие с согласованностью.
Но Лейтенант 2 (из симметрии) будет отступать! Противоречие с согласованностью.

Слайд 19Протокол византийского соглашения
Протокол решения данной задачи называется протоколом византийского соглашения (byzantine agreement.)
Протокол византийского соглашения
Протокол решения данной задачи называется протоколом византийского соглашения (byzantine agreement.)

1. Условие завершения. Все честные участники вычислений в конце протокола принимают значение d.
2. Условие корректности. Если существует значение x такое, что для честных участников xi=x, тогда d=x.
«Задача византийского соглашения» формулируется на основе «задачи о византийских генералах»: для n взаимодействующих генералов нужно предложить такой протокол взаимодействия, чтобы при наличии среди них m «нелояльных» генералов остальные генералы – «лояльные», – имея каждый свое мнение, всегда вырабатывали согласованную общую позицию (например, штурмовать крепость или нет). В протоколе все генералы по очереди выступают в роли командующего, они рассылают свое мнение и собирают мнения остальных в роли подчиненного. В этом заключается принцип решения даной задачи. Все честные генералы получают в итоге одинаковый результат, это гарантирует процедура голосования по мажоритарному принципу. При пересылке подписанных и неподписанных сообщений, способы решения задачи различны.
На протоколе византийского соглашения базируется построение большого количества других протоколов: достижения консенсуса, частичного соглашения гарантированной широковещательной рассылки и др. Каждый год появляется большое количество новых протоколов, которые решают еще более сложные задачи защиты распределенных систем.
Таким образом, недавно был предложен новый метод обнаружения «лжецов», квантовый. Он является вариантом «Византийского соглашения».
Пример этой схемы: Соглашение нескольких генералов, некоторые из них подкуплены, о необходимости атаковать вместе или отступить. Цель противника: отступление части генералов, для успешной победы над оставшимися.
Слайд 20Схема «Византийского соглашения» с использованием квантовых коммуникаций
Схема «Византийского соглашения» с использованием квантовых
Схема «Византийского соглашения» с использованием квантовых коммуникаций
Схема «Византийского соглашения» с использованием квантовых

Этот протокол дает возможность найти согласованное решение и определить возможного «лжеца» из трех участников, которые обмениваются сообщениями. Так же как и любое другое «Византийское соглашение», можно сказать, что этот протокол сводится к обеспечению:
1. Все участники получают один и тот же план
2. У плана есть определенный автор, и если он незлонамеренен, то все соглашаются с ним и следуют его плану.
Для того чтобы успешно реализовать «Византийского соглашения», нужно, чтобы у всех участников были наборы чисел, которые связаны между собой, но не известны другим. Этот протокол позволяет безопасную генерацию и дистрибуцию таких чисел и обнаружение «лжеца» с помощью квантовых каналов связи.
Чаще всего, сложность реализации квантовых протоколов между более чем двумя участниками заключается в необходимости использования кутритов. Трудно контролировать физические носители кутритов, например, сложно реализовывать из передачу. Но исследователи смогла не использовать кутриты, и вместо них использовала в качестве носителей кубитов четыре поляризованных фотона. Исследователи задействовали фотоны, которые находятся в запутанном квантовом состоянии. Иначе говоря, фотоны имеют коррелированные квантовые свойства после взаимодействия и разделения.Такие фотоны были использовались для дистрибуции ключей, которые применяются в верификационном процессе.
Слайд 21
Предложен квантовый метод обнаружения «лжецов»
http://rnns.ru/5175-predlozhen-kvantovyjj-metod.html
Предложен квантовый метод обнаружения «лжецов»
http://rnns.ru/5175-predlozhen-kvantovyjj-metod.html

Слайд 22В 1985-1986 гг., понимание различных протоколов и способов их построения привело к
В 1985-1986 гг., понимание различных протоколов и способов их построения привело к

1) полнота — если S действительно истинно, то абонент P почти наверняка убедит абонента V признать это;
2) корректность — если S ложно, то абонент P вряд ли убедит абонента V, что S истинно.
В определении системы (P, V, S) не допускалось, что V может быть противником. В случае, если V оказался противником, который хочет получить от Р новую информацию об утверждении S, P, естественно, может не хотеть, чтобы это случилось в результате работы протокола (P, V,S). Протокол (P, V, S), который решает такую задачу, называется доказательством с нулевым разглашением. Он должен удовлетворять еще одному условию:
3) нулевое разглашение (или стойкость) — в результате работы протокола (P, V, S) абонент V не увеличит свои знания об утверждении S или, другими словами, не сможет извлечь никакой информации о том, почему S истинно.
В 1991 году для большого класса математических проблем (включающего так называемые NP-полные задачи) получилось доказать существование доказательств с нулевым разглашением. Но это доказано только в предположении, что существует односторонняя функция.
«Интеллектуальные карточки» (кредитные карточки, не подделываемые удостоверения и т. п.) - практическое применение теории доказательств с нулевым разглашением. В них есть микропроцессор, который реализует действия участника Р в протоколе, который претендует быть протоколом доказательства с нулевым разглашением (P, V, S), где P — владелец карточки, V — может быть компьютером в банке или в проходной секретного учреждения.




 Работа в среде TRIK Studio
Работа в среде TRIK Studio Координаты аэропортов
Координаты аэропортов Интеграционная платформа. Отраслевой стандарт обработки данных
Интеграционная платформа. Отраслевой стандарт обработки данных Проект. Григорианский пролептический календарь
Проект. Григорианский пролептический календарь Канал https://www.youtube.com/wat ch?v=FhMOcFGyQas&t=20s
Канал https://www.youtube.com/wat ch?v=FhMOcFGyQas&t=20s Антивирус VSafe
Антивирус VSafe Понятие информации. (Вводная)
Понятие информации. (Вводная) Binding event handlers
Binding event handlers Инструменты Яндекса для сложных цепочек коммуникаций с клиентами
Инструменты Яндекса для сложных цепочек коммуникаций с клиентами Воины казармы
Воины казармы Zanyatie_2
Zanyatie_2 Разработка игры по технике безопасности на предприятии (организации)
Разработка игры по технике безопасности на предприятии (организации) Производственная практика на телеканале Хузур-Спокойствие
Производственная практика на телеканале Хузур-Спокойствие Устройство компьютера. 5 класс
Устройство компьютера. 5 класс Программное обеспечение компьютера
Программное обеспечение компьютера 8-2-3
8-2-3 Mobile SMARTS. Интеграция с 1С-Предприятием
Mobile SMARTS. Интеграция с 1С-Предприятием Анализ соцсети
Анализ соцсети Персональные данные
Персональные данные Компьютерная графика
Компьютерная графика Географические информационные системы
Географические информационные системы Основные принципы организации СС
Основные принципы организации СС Разработка музыкального сайта
Разработка музыкального сайта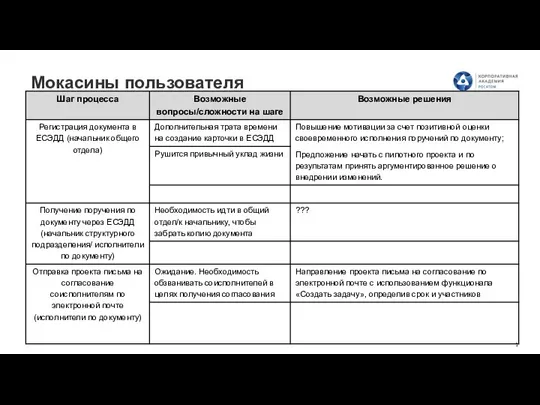 Мокасины пользователя
Мокасины пользователя Автоматическая система теплопотребления и погодного регулирования в ИТП многоквартирного дома
Автоматическая система теплопотребления и погодного регулирования в ИТП многоквартирного дома Презентация на тему Устройства ввода информации
Презентация на тему Устройства ввода информации  Приведение ER-диаграммы к реляционному виду
Приведение ER-диаграммы к реляционному виду Интернет как один из источников информационного обеспечения фундаментальных и прикладных научных исследований
Интернет как один из источников информационного обеспечения фундаментальных и прикладных научных исследований