Слайд 2Логика:
Формальная логика- наука, пытавшаяся найти ответ на вопрос, как мы рассуждаем, изучающая

логические операции и правила мышления.
Математическая логика- раздел математики, изучающий булеву алгебру, алгебру отношений, теорию доказательств.
Слайд 3Правила:
Исходить из достоверных положений
Сводить сложные идеи к простым
Переходить от известного и доказанного

к неизвестному, избегая каких-либо пропусков в логических звеньях исследований
Слайд 4Булевы переменные
Булева переменная- переменная, которая может принимать только два значения: 0

или 1.
При любых комбинациях значений булевых переменных булева функция будет принимать только два значения:
0 иногда называют «Ложь» или «False»
1 иногда называют «Истина» или «True»
Слайд 5Для булевых переменных определены следующие операции:
Логическое НЕ (инверсия); обозначают: чертой над переменной
Логические

связи- функции, аргументами которых являются простые высказывания.
Логическое И (конъюнкция); обозначают: &, Л
Логическое ИЛИ (дизъюнкция); обозначают: |,V
Логическое ИСКЛЮЧАЮЩЕЕ ИЛИ (строгая дизъюнкция); обозначают: перевернутая буква «А» или плюсик в кружечке
Слайд 6Таблица истинности
Таблица истинности- таблица, устанавливающая соответствие между возможными значениями набора переменных

и значениями функции.
Таблицы истинности логических функций позволяют определить значения, которые принимают эти функции при различных значениях переменных, сравнивать функции между собой, определять, удовлетворяют ли функции заданным свойствам.
Слайд 7Из таблицы истинности можно сделать следующие выводы:
Только операция НЕ применяется к одной

переменной
Таблица истинности для конъюнкции совпадает с таблицей умножения, поэтому конъюнкцию можно назвать произведением
Смысл союза «или», принятого в русском языке как разъединение, в дизъюнкции изменяется на противоположный, и тот союз употребляется в смысле объединения
Выполняются все операции НЕ
Выполняются все операции И
Выполняются все операции ИЛИ и ИСКЛЮЧАЮЩЕЕ ИЛИ






 Комбинация данных из нескольких таблиц
Комбинация данных из нескольких таблиц Целевая рассылка Сенлер
Целевая рассылка Сенлер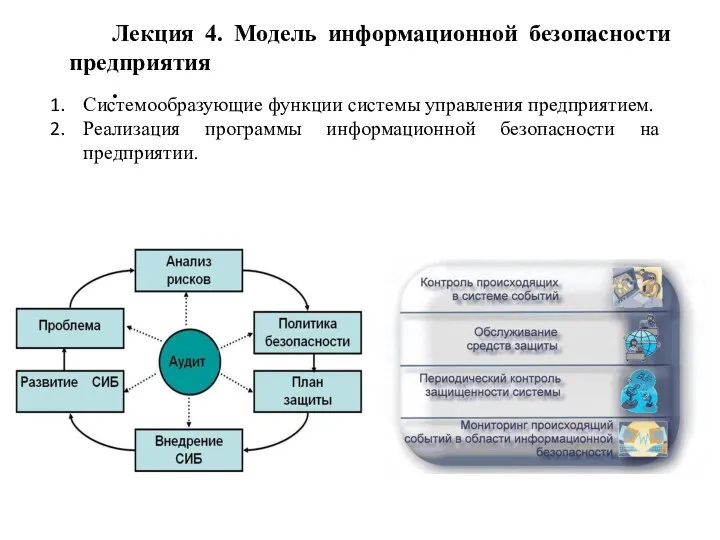 Модель информационной безопасности предприятия
Модель информационной безопасности предприятия Городские сообщества Севастополя
Городские сообщества Севастополя Виды угроз компьютерной информации
Виды угроз компьютерной информации Компьютерный мир
Компьютерный мир Получении информации через компьютерные технологии
Получении информации через компьютерные технологии EW2-week 1
EW2-week 1 Система автоматического проектирования AutoСad (часть 1)
Система автоматического проектирования AutoСad (часть 1) Информационная безопасность компьютерных систем и сетей
Информационная безопасность компьютерных систем и сетей Количество путей в графе
Количество путей в графе Алгоритмы. Потенциометр. COM-порт
Алгоритмы. Потенциометр. COM-порт Машинное обучение на языке программирования Python
Машинное обучение на языке программирования Python Оптимизация обновления информационной базы. Информация для технических специалистов
Оптимизация обновления информационной базы. Информация для технических специалистов СУБД ACCESS. Создание таблиц, запросов. (Лекция 4-2)
СУБД ACCESS. Создание таблиц, запросов. (Лекция 4-2) Алгоритмический язык стрелок для создания циклического алгоритма
Алгоритмический язык стрелок для создания циклического алгоритма تطبيق أمانتي
تطبيق أمانتي Занятия Блокли
Занятия Блокли ТЕМА: «ОПЕРАТОР ВЫБОРА CASE»
ТЕМА: «ОПЕРАТОР ВЫБОРА CASE» Основы телекоммуникаций сетей. Технологии телекоммуникационных сети TCP/IP
Основы телекоммуникаций сетей. Технологии телекоммуникационных сети TCP/IP Основы логики
Основы логики Презентация на тему История развития отечественной вычислительной техники
Презентация на тему История развития отечественной вычислительной техники  Рисуем снежинку. Занятие по программе Paint
Рисуем снежинку. Занятие по программе Paint Использование внешних устройств, подключаемых к компьютеру, в учебных целях. Программное обеспечение внешних устройств
Использование внешних устройств, подключаемых к компьютеру, в учебных целях. Программное обеспечение внешних устройств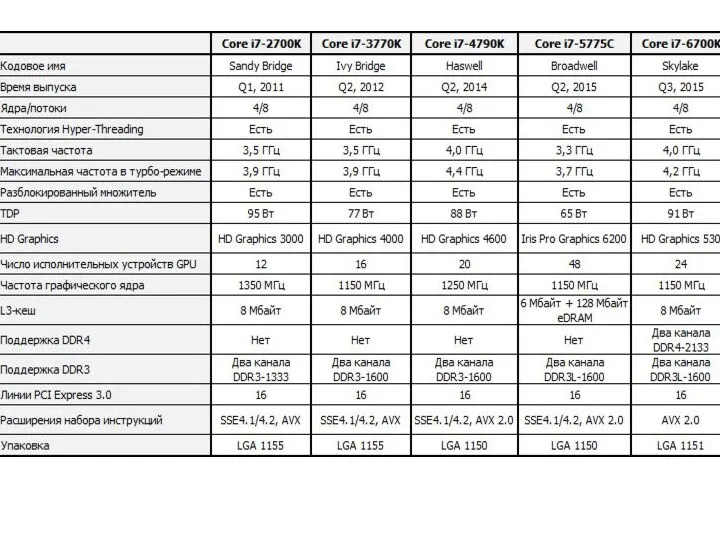 SYSmark 2014. Тестирование процессоров
SYSmark 2014. Тестирование процессоров Анимированные ребусы
Анимированные ребусы Нарисуйте домик в стиле пиксел арт
Нарисуйте домик в стиле пиксел арт Команды ветвления
Команды ветвления