Содержание
- 2. Алгебра логики Логическая функция – это функция, у которой значения переменных и значение функции выражают логическую
- 3. Алгебра логики 1. Конъюнкция (логическое умножение) – сложное логическое выражение, которое является истинным только в том
- 4. Алгебра логики 2. Дизъюнкция является сложным логическим выражением, которое истинно практически всегда, за исключением, когда все
- 5. Алгебра логики 3. Импликация - это сложное логическое выражение, которое истинно во всех случаях, кроме как
- 6. Алгебра логики 4. Эквивалентность - это сложное логическое выражение, которое истинно на равных значениях переменных A
- 7. Алгебра логики 5. Отрицание(инверсия) - означает, что к исходному логическому выражению добавляется частица НЕ или слова
- 8. Алгебра логики Штрих Шеффера Булева функция двух переменных или бинарная логическая операция. Обозначения: |, эквивалентно операции
- 9. Алгебра логики Порядок выполнения логических операций в сложном логическом выражении Инверсия(отрицание); Конъюнкция (логическое умножение); Дизъюнкция и
- 10. Алгебра логики Построим таблицу истинности A∨A&B. В нём две переменные, две операции, причём сначала выполняется конъюнкция,
- 11. Задание 1. ! Построить таблицу истинности и решить выражение F=(A∨B)∧(¬A∨¬B). В помощь приведённый ниже алгоритм. Число
- 13. Скачать презентацию










 Проектирование сетей. Общие положения
Проектирование сетей. Общие положения Диаграмма деятельности
Диаграмма деятельности Введение в CSS. Блочная верстка.. Занятие 2
Введение в CSS. Блочная верстка.. Занятие 2 Медиапланирование и мониторинг СМИ
Медиапланирование и мониторинг СМИ IT технологии в гостницах
IT технологии в гостницах Физический уровень компьютерных сетей
Физический уровень компьютерных сетей WISE² Close-out Meeting
WISE² Close-out Meeting Хранение информации (7 класс)
Хранение информации (7 класс) Briefing designers
Briefing designers Лексика интернета
Лексика интернета 1666607538405__u5jj0u
1666607538405__u5jj0u Slides on lists. Operation on lists
Slides on lists. Operation on lists Python. Регулярные выражения
Python. Регулярные выражения Социальная сеть как основа современной социальной структуры
Социальная сеть как основа современной социальной структуры Язык программирования Паскаль
Язык программирования Паскаль 20140111_didakticheskie_vozmozhnosti_metodov_i_priyomov_obucheniya_geografii
20140111_didakticheskie_vozmozhnosti_metodov_i_priyomov_obucheniya_geografii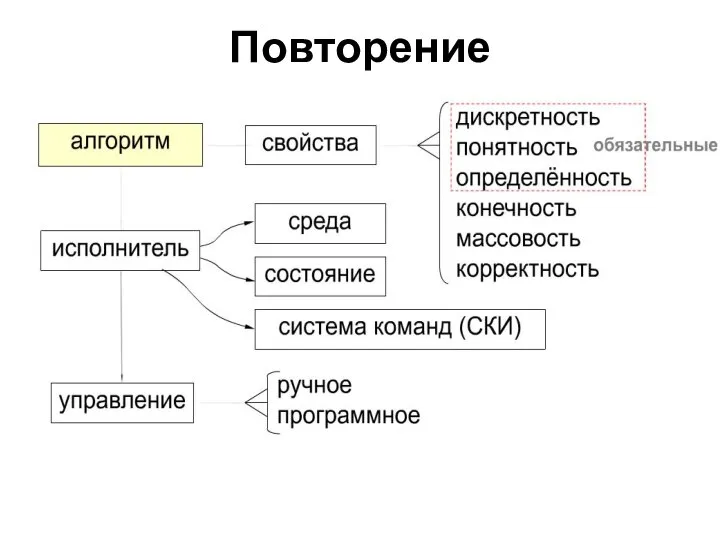 Алгоритмы и исполнители. Решение задач
Алгоритмы и исполнители. Решение задач Безопасность в сети для 2-4 классов
Безопасность в сети для 2-4 классов Базы данных. СУБД
Базы данных. СУБД Эффективные методы управления безопасностью для линейных руководителей
Эффективные методы управления безопасностью для линейных руководителей Инстаграм от А до Я
Инстаграм от А до Я Лекции по информатике (часть 1)
Лекции по информатике (часть 1) Подробное ТЗ для создания видео-отчета
Подробное ТЗ для создания видео-отчета Основы композиционного построения. Имитация техник графического дизайна. Понятие цвета и его представления в компьютерном
Основы композиционного построения. Имитация техник графического дизайна. Понятие цвета и его представления в компьютерном Мир здоровья и страхования в одной программе на ладони смартфона
Мир здоровья и страхования в одной программе на ладони смартфона Создание системы автоматизированного проектирования Optical constructor
Создание системы автоматизированного проектирования Optical constructor Обробка фотографій на ПК
Обробка фотографій на ПК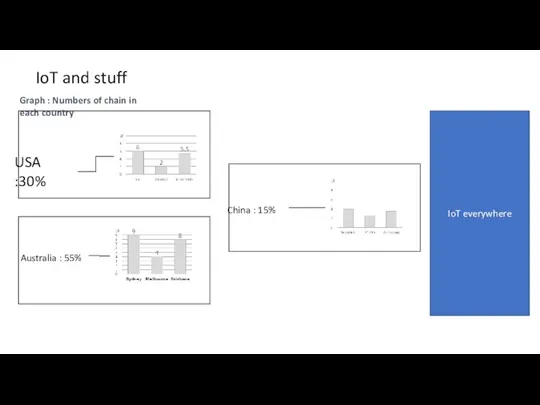 Numbers of chain in each country
Numbers of chain in each country