Преобразования комплексного чертежа. Способ замены плоскостей проекций. Основные метрические задачи. (Лекция 3)

06.10.2021
Лекция 3
Лекция 3
Преобразования комплексного чертежа.
Способ замены плоскостей проекций.
Основные метрические задачи.

Содержание
Способы преобразования комплексного чертежа;
Четыре основные задачи преобразования чертежа;
Определение угла наклона плоскости к плоскостям проекций;
Линии наибольшего наклона плоскости;
Решение метрических задач преобразованиями комплексного чертежа..
06.10.2021
Лекция 3

Основные графические задачи
Все графические задачи условно делятся на 2 класса.
1-й класс – задачи позиционные;
2-й класс – задачи метрические.
Позиционными называются такие задачи, в которых определяется взаимное расположение различных геометрических фигур относительно друг друга.
06.10.2021
Лекция 3

Метрические задачи
Метрическими (от греческих слов metron –мера, metreo - мерить)называются задачи, решение которых связано с нахождением характеристик геометрических фигур, определяемых (измеряемых) линейными и угловыми величинами. К метрическим характеристикам относят длины участков линий, величины углов, площадей, объемов и т.п.
Наиболее сложные задачи, при решении которых используют как метрические, так и позиционные свойства геометрических фигур, называют комплексными.
06.10.2021
Лекция 3

06.10.2021
Лекция 3

Все метрические задачи сводятся к двум видам:
А) задачи на определение расстояния между двумя точками;
Б) задачи на нахождение величины угла между двумя пересекающимися прямыми.
Решать такие задачи удобно с помощью различных способов преобразования комплексного чертежа.
06.10.2021
Лекция 3

06.10.2021
Лекция 3
Определение расстояния между двумя точками отрезка прямой и углов наклона отрезка способом прямоугольного треугольника
Натуральная величина отрезка равна гипотенузе прямоугольного треугольника, построенного на двух катетах один из которых проекция отрезка, а второй – разница координат начала и конца отрезка в другой плоскости проекций.

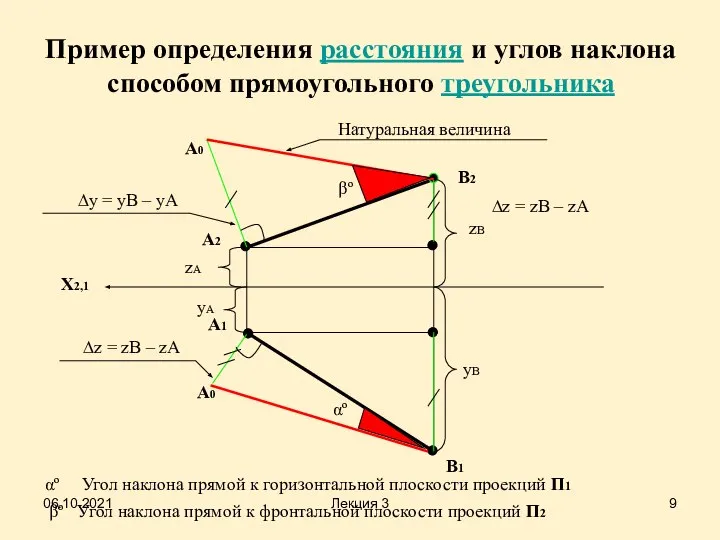
Пример определения расстояния и углов наклона способом прямоугольного треугольника
X2,1
A2
B2
B1
A1
A0
A0
αº
βº
Натуральная величина
yA
yB
∆y = yB – yA
zB
zA
∆z = zB – zA
αº
Угол наклона прямой к горизонтальной плоскости проекций П1
βº Угол наклона прямой к фронтальной плоскости проекций П2
∆z = zB – zA
06.10.2021
Лекция 3

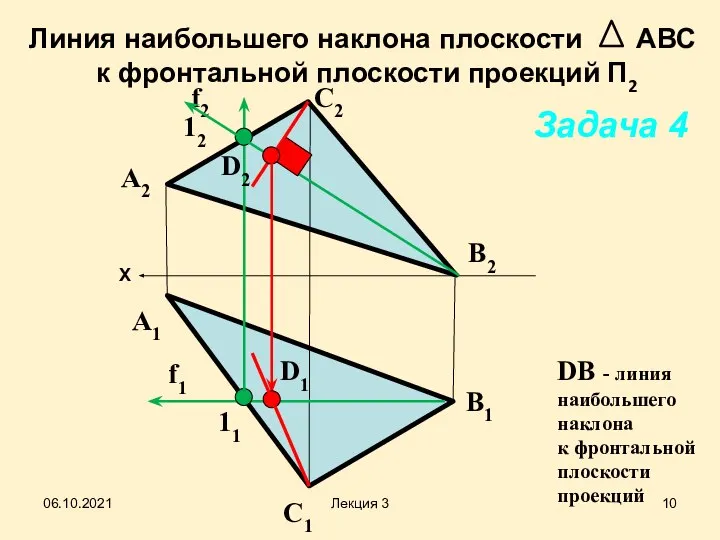
Х
Линия наибольшего наклона плоскости АВС
к фронтальной плоскости проекций П2
В1
В2
A1
C1
C2
A2
12
f2
f1 11
DВ - линия
наибольшего
наклона
к фронтальной
плоскости
проекций
D2
D1
Задача 4
06.10.2021
Лекция 3

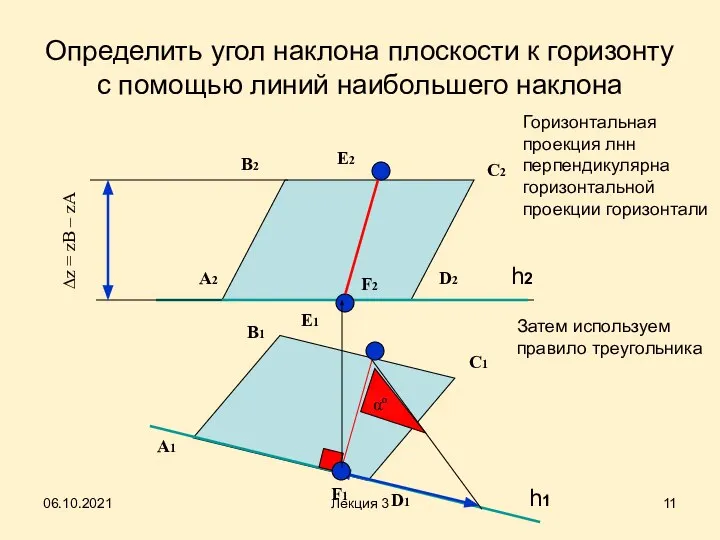
Определить угол наклона плоскости к горизонту с помощью линий наибольшего наклона
A2
B2
B1
A1
С2
D2
С1
D1
Е2
Е1
Горизонтальная
проекция лнн
перпендикулярна
горизонтальной
проекции горизонтали
h1
h2
Затем используем
правило треугольника
∆z = zB – zA
αº
F2
F1
06.10.2021
Лекция 3

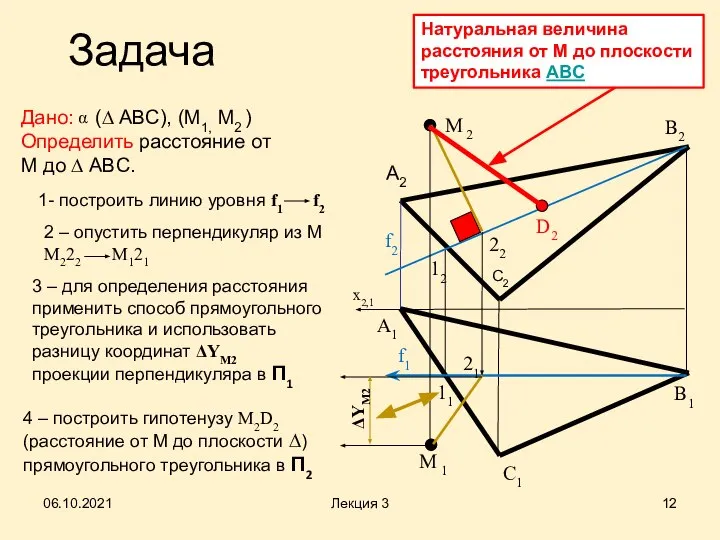
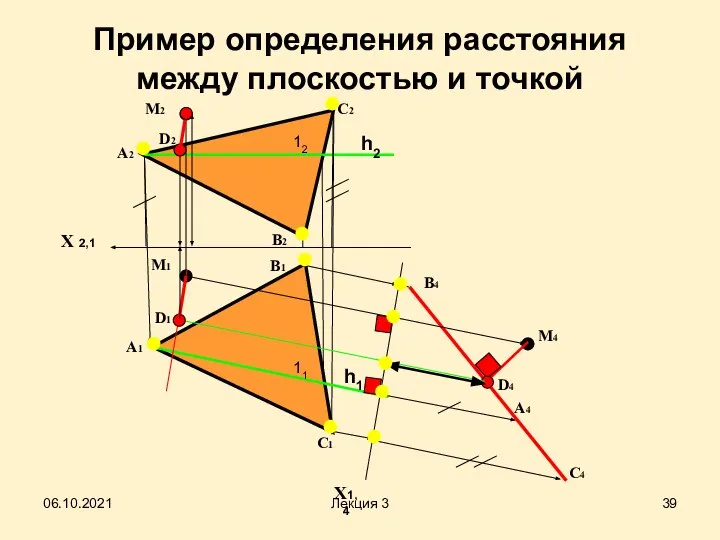
Задача
Дано: (∆ ABC), (М1, М2 )
Определить расстояние от М до ∆ ABC.
α
A1
B2
B1
C1
М 2
М 1
x2,1
A2
C2
06.10.2021
Лекция 3
f2
f1
12
11
22
21
D2
ΔYM2
1- построить линию уровня f1 f2
2 – опустить перпендикуляр из М
М222 М121
3 – для определения расстояния
применить способ прямоугольного
треугольника и использовать разницу координат ΔYM2
проекции перпендикуляра в Π1
4 – построить гипотенузу М2D2 (расстояние от М до плоскости ∆)
прямоугольного треугольника в Π2
Натуральная величина
расстояния от М до плоскости
треугольника АВС

Пересечение линии с плоскостью(поверхностью)
Задача сводится к решению задачи на определение точки, принадлежащей прямой и поверхности.
Для решения необходимо:
1) через одну из проекций прямой провести конкурирующую прямую, принадлежащую поверхности;
2) найти ее проекцию во второй плоскости проекций.
Если эта проекция пересечет проекцию заданной прямой, значит имеется точка пересечения прямой и поверхности.
06.10.2021
Лекция 3

Способы преобразования комплексного чертежа
Исходный чертеж не всегда удобен для решения позиционных и метрических задач. В этих случаях чертеж преобразуют так, чтобы новый (преобразованный) чертеж позволил получить нужное решение без сложных геометрических построений.
06.10.2021
Лекция 3

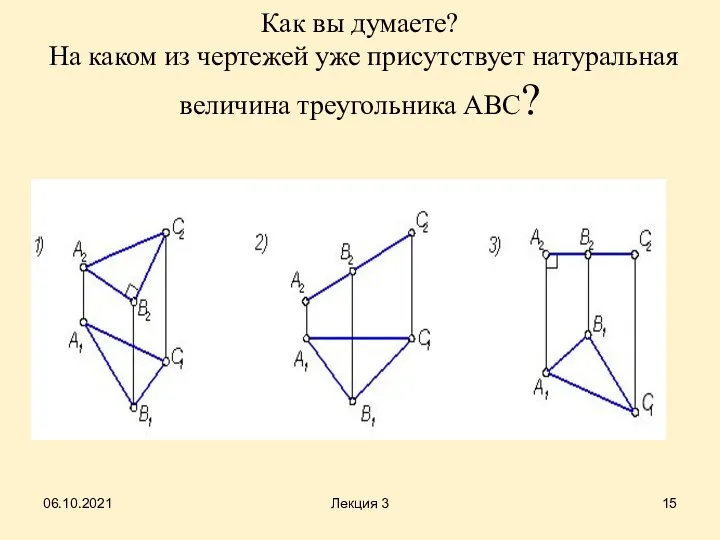
Как вы думаете?
На каком из чертежей уже присутствует натуральная величина треугольника АВС?
06.10.2021
Лекция 3

06.10.2021
Лекция 3
Проецируемая фигура может занимать по отношению к плоскостям проекций
произвольное или
частное положение.
В первом случае, как правило, получаются проекции неудобные для решения задач.
Решение значительно упрощается, если фигура оказывается в частном положении относительно плоскости проекций.

Наиболее выгодным частным положением проецируемой фигуры следует считать:
1) положение, перпендикулярное к плоскости проекций – при решении позиционных задач;
2) положение, параллельное плоскости проекций – для решения метрических задач.
06.10.2021
Лекция 3

Метрические задачи
Метрическими (от греческих слов metron –мера, metreo - мерить)называются задачи, решение которых связано с нахождением характеристик геометрических фигур, определяемых (измеряемых) линейными и угловыми величинами. К метрическим характеристикам относят длины участков линий, величины углов, площадей, объемов и т.п.
Наиболее сложные задачи, при решении которых используют как метрические, так и позиционные свойства геометрических фигур, называют комплексными.
06.10.2021
Лекция 3

Все метрические задачи сводятся к двум видам:
А) задачи на определение расстояния между двумя точками;
Б) задачи на нахождение величины угла между двумя пересекающимися прямыми.
Решать такие задачи удобно с помощью различных способов преобразования комплексного чертежа.
06.10.2021
Лекция 3

Задачи на преобразование комплексного чертежа
Преобразование прямой общего
положения в прямую уровня.
2. Преобразование прямой общего положения в прямую
проецирующую.
3. Преобразование плоскости общего
положения в плоскость
проецирующую.
4. Преобразование плоскости общего
положения в плоскость уровня.
06.10.2021
Лекция 3

Основные принципы и последовательность решения метрических задач
Алгоритмы решения всех метрических задач опираются на два инварианта ортогонального проецирования:
1. Теорему (прямую и обратную) о проецировании прямого угла;
2. Свойство любой плоской фигуры проецироваться без искажения, в конгруэнтную фигуру, на ту плоскость проекций, которая параллельна этой фигуре.
06.10.2021
Лекция 3

Для решения задач предлагается следующая последовательность:
Первый этап. Сосредоточиться и осмыслить постановку задачи. Что дано? Что требуется? Какие ставятся условия и возможно ли их выполнить?
Второй этап. Поиск связи между исходными данными и искомыми.
Третий этап. Реализация (графическая) плана; здесь необходим контроль правильности решения и точности графических операций.
Завершающий этап. Анализ решения задачи – при каких условиях и сколько решений возможно.
06.10.2021
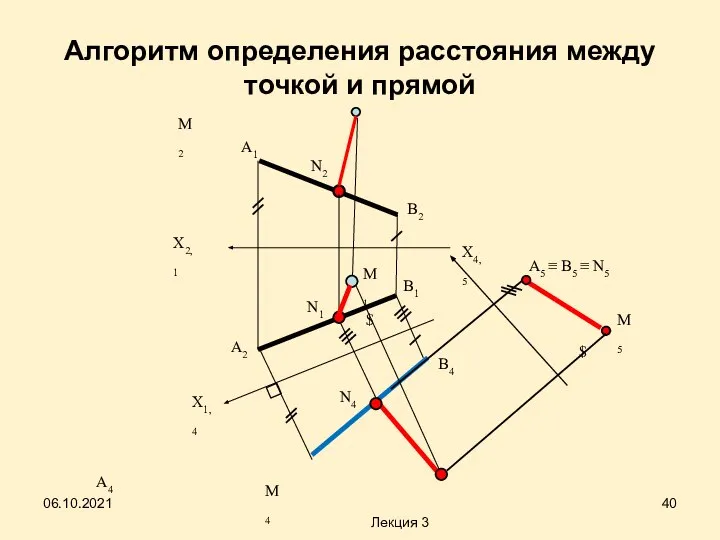
Лекция 3

Определение расстояний
Решение задач на определение расстояний между точкой и прямой, двумя параллельными прямыми, точкой и плоскостью, прямой и плоскостью, двумя плоскостями, скрещивающимися прямыми в конечном счете сводится к нахождению расстояния между точками.
06.10.2021
Лекция 3

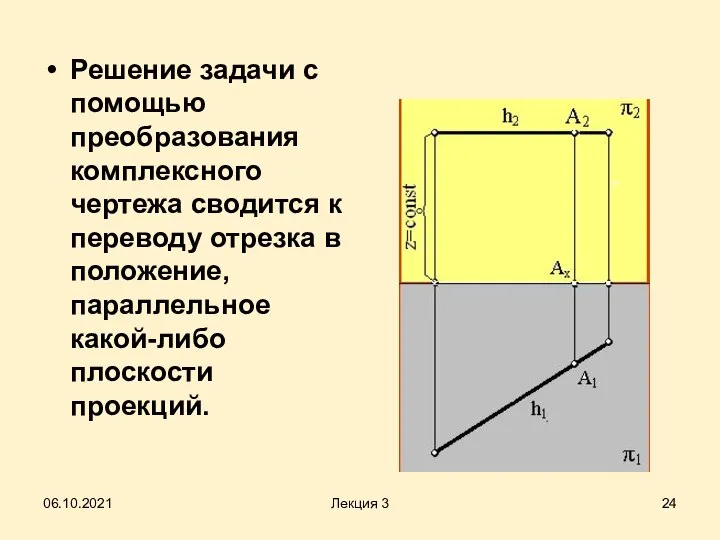
Решение задачи с помощью преобразования комплексного чертежа сводится к переводу отрезка в положение, параллельное какой-либо плоскости проекций.
06.10.2021
Лекция 3

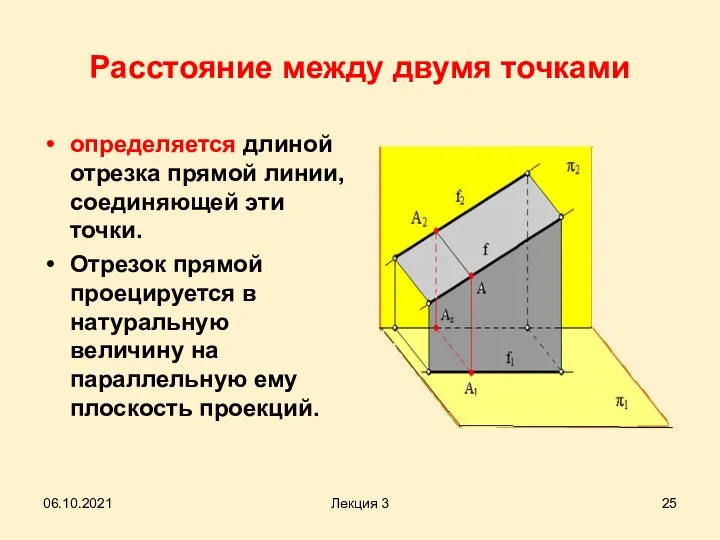
Расстояние между двумя точками
определяется длиной отрезка прямой линии, соединяющей эти точки.
Отрезок прямой проецируется в натуральную величину на параллельную ему плоскость проекций.
06.10.2021
Лекция 3

Пути преобразования комплексного чертежа
Изменение положения объекта относительно плоскостей проекций.
2. Изменение положения плоскостей проекций относительно объекта.
06.10.2021
Лекция 3

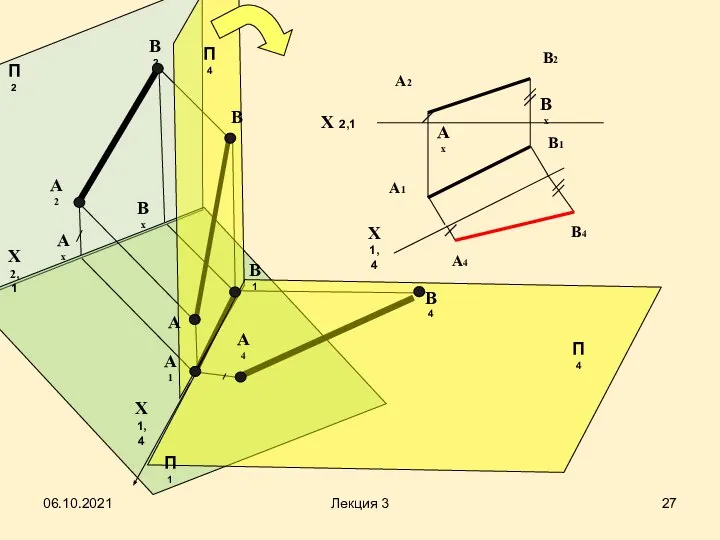
П4
П4
X1,4
П1
П2
A2
Ax
Bx
B2
A4
B4
Bx
Ax
B
А
X2,1
A1
B1
Х 2,1
А2
В2
X1,4
А1
В1
А4
В4
06.10.2021
Лекция 3

Задачи на преобразование комплексного чертежа
Преобразование прямой общего
положения в прямую уровня.
2. Преобразование прямой общего положения в прямую
проецирующую.
3. Преобразование плоскости общего
положения в плоскость
проецирующую.
4. Преобразование плоскости общего
положения в плоскость уровня.
06.10.2021
Лекция 3

Определение расстояния между двумя точками (Задача 1)
Для решения задачи необходимо заменить плоскость проекций П1, или П2 новой плоскостью проекций П4, параллельной прямой АВ и перпендикулярной к незаменяемой плоскости проекций. Для того чтобы прямая АВ в новой системе плоскостей проекций стала, например, фронталью, нужно заменить фронтальную плоскость проекций П2 новой плоскостью П4 П1 и параллельной прямой АВ.
Отрезок [АВ] прямой проецируется на плоскость П4 в истинную величину, т.е. | А4В4 | = | АB |, α- величина угла наклона прямой АВ к плоскости П1.
06.10.2021
Лекция 3

Алгоритм решения первой задачи
Для решения первой основной задачи на преобразование комплексного чертежа:
1) провести новую ось проекций х1,4 параллельно А1В1 на произвольном расстоянии от нее;
такое положение оси х1,4 обусловливается тем, что П4 параллельна АВ. В частном случае, если плоскость П4 проведена непосредственно через прямую АВ, ось х1,4 = А1В1;
06.10.2021
Лекция 3

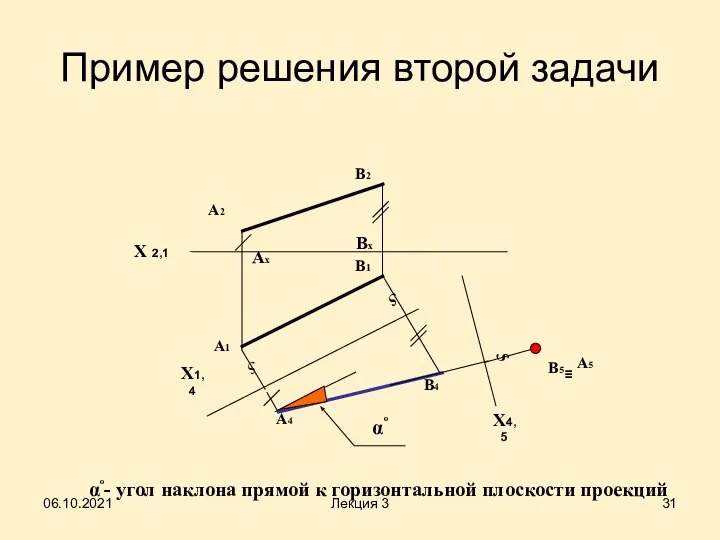
Пример решения второй задачи
Bx
Ax
Х 2,1
А2
В2
X1,4
А1
В1
А4
В4
X4,5
ς
ς
ς
В5
А5
≡
αº
αº- угол наклона прямой к горизонтальной плоскости проекций
06.10.2021
Лекция 3

Алгоритм решения второй задачи
Построения на комплексном чертеже: 1) проводим новую ось проекций х14 // А1В1;
2) построим проекции точек А и В на плоскости П4, взяв координаты точек из плоскости П2.
3) Заменим плоскость П1 на новую П5, которая будет П4 и А4В4. Для этого проводим новую ось проекций х4,5. Так как расстояния точек А и В до плоскости П4 одинаковы, то проекции их на плоскости П5 совпадут, А5 ≡ В5.
Прямая АВ (А5В5) в новой системе плоскостей проекций заняла проецирующее положение и является горизонтально проецирующей. Для того чтобы прямую общего положения преобразовать в проецирующую, необходимо выполнить две последовательные замены плоскостей проекций. Вначале прямую следует преобразовать в линию уровня, а затем линию уровня преобразовать в проецирующую.
06.10.2021
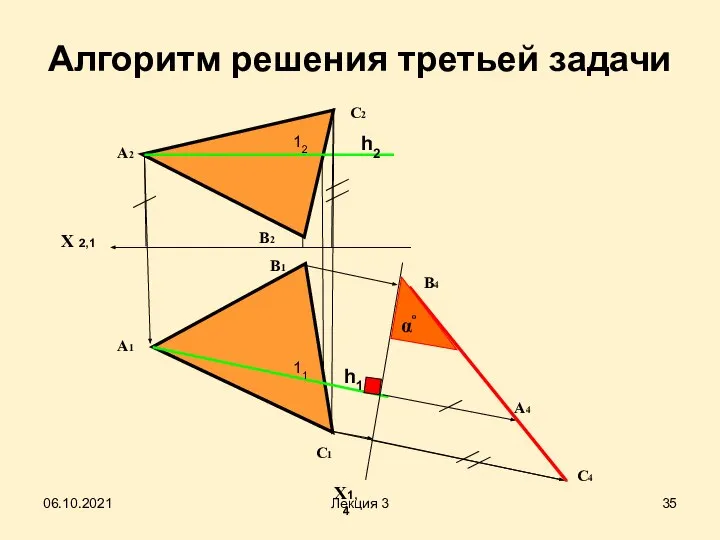
Лекция 3

Алгоритм решения третьей задачи
Для решения задачи необходимо заменить плоскость П1 или П2 исходной системы П2/П1 новой плоскостью П4, перпендикулярной плоскости (АВС). Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную к другой плоскости. Следовательно, если какую-либо прямую, принадлежащую плоскости , преобразовать в проецирующую, то плоскость в новой системе плоскостей проекций станет проецирующей. Проще всего для этой цели воспользоваться линией уровня.
06.10.2021
Лекция 3

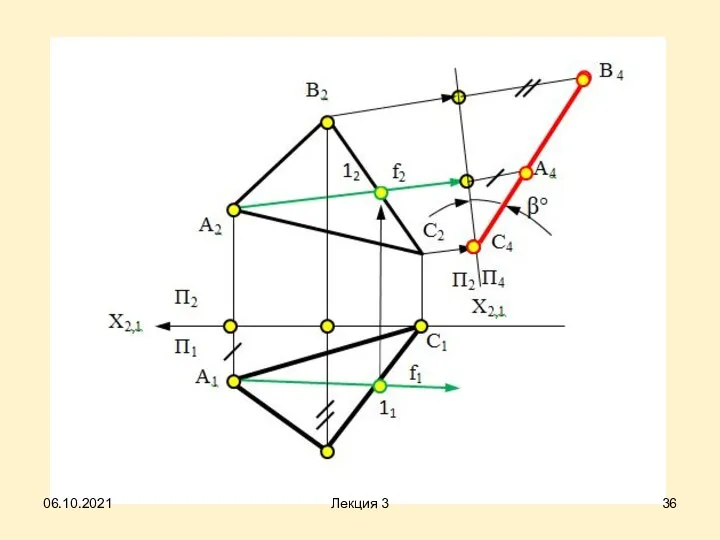
На чертеже плоскость (АВС) преобразована во фронтально проецирующую путем преобразования горизонтали h(h1,h2), принадлежащей плоскости , во фронтально- проецирующую прямую. В новой системе плоскостей проекций П1/П4 плоскость является фронтально проецирующей ( 4), и поэтому ее проекция на П4 вырождается в прямую линию 4 (С4, А4, В4).
- величина угла наклона плоскости к плоскости П1.
αº
06.10.2021
Лекция 3

Алгоритм решения третьей задачи
Х 2,1
А2
X1,4
А1
В1
А4
В4
С4
С1
С2
В2
h1
h2
11
12
αº
06.10.2021
Лекция 3

06.10.2021
Лекция 3

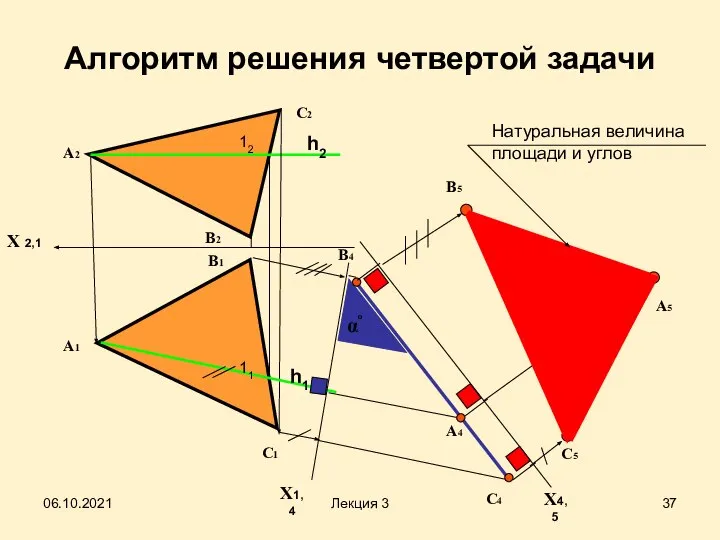
Алгоритм решения четвертой задачи
Х 2,1
А2
X1,4
А1
В1
А4
В4
С4
С1
С2
В2
h1
h2
11
12
αº
X4,5
С5
А5
В5
Натуральная величина площади и углов
06.10.2021
Лекция 3

06.10.2021
Лекция 3

Пример определения расстояния между плоскостью и точкой
Х 2,1
А2
X1,4
А1
В1
А4
В4
С4
С1
С2
В2
h1
h2
11
12
М1
М2
М4
D4
D1
D2
06.10.2021
Лекция 3

Алгоритм определения расстояния между точкой и прямой
$
$
А1
А2
N1
А4
В2
В1
В4
М1
М2
М4
М5
N2
N4
X2,1
X1,4
X4,5
А5 ≡ B5 ≡ N5
06.10.2021
Лекция 3

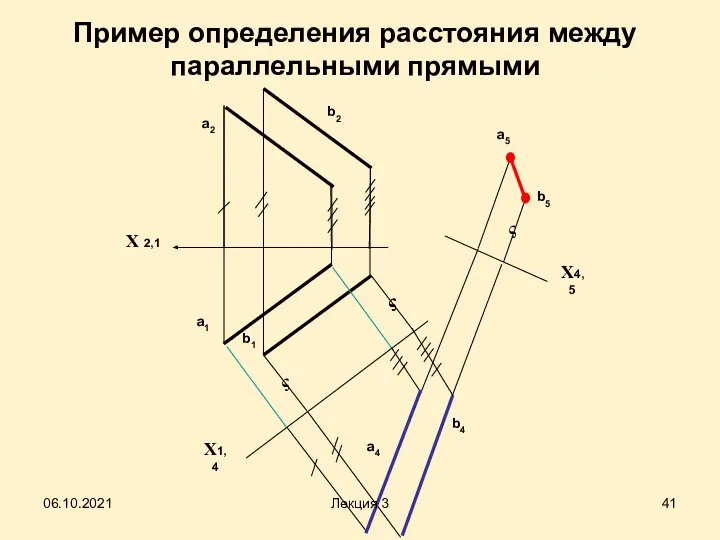
Пример определения расстояния между параллельными прямыми
Х 2,1
а1
а2
b1
b2
X1,4
а4
b4
X4,5
ς
ς
ς
ς
а5
b5
06.10.2021
Лекция 3

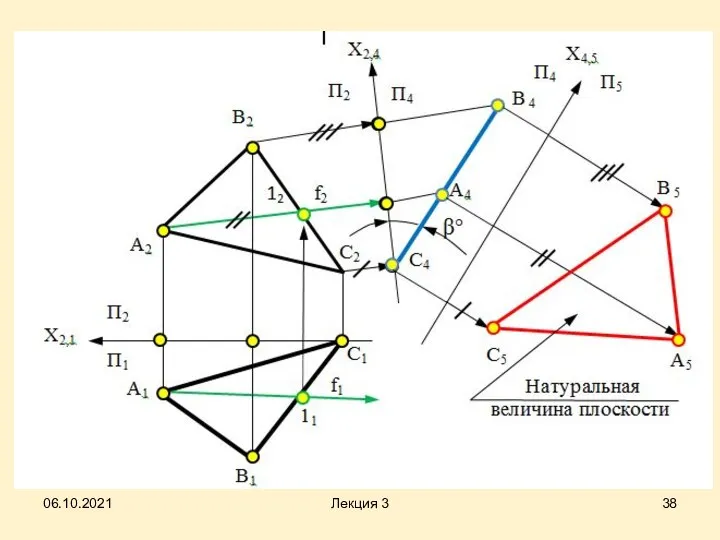
Алгоритм решения четвертой задачи
Плоскость общего положения преобразовать в плоскость уровня заменой только одной плоскости проекций нельзя, так как плоскость П4, параллельная ей, не будет перпендикулярна ни одной из старых плоскостей проекций и, следовательно, не образует ни с одной из них прямоугольной системы плоскостей проекций.
06.10.2021
Лекция 3

Для того чтобы плоскость общего положения преобразовать в плоскость уровня, необходимо выполнить две последовательные замены плоскостей проекций.
Вначале плоскость необходимо преобразовать в проецирующую, т. е. решить задачу 3,
а затем проецирующую плоскость преобразовать в плоскость уровня.
На рис. показано преобразование плоскости ∆(АВС) в горизонтальную плоскость уровня.
2
06.10.2021
Лекция 3

До свидания.
Спасибо за внимание.
Лекция 3
06.10.2021

Лекцию составил Ведякин Фёдор Филиппович
Лекция 3
06.10.2021

Контрольная работа №2
Тема: «Задачи метрические»
06.10.2021
Лекция 3

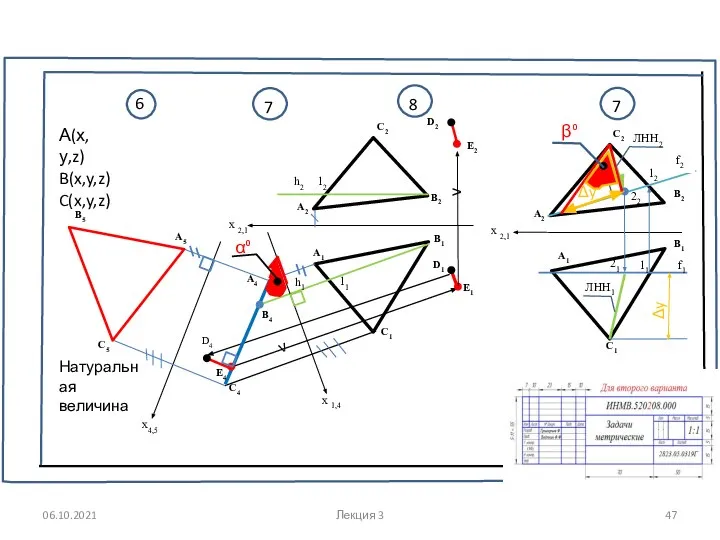
h2
С2
А2
В2
С1
А1
В1
х 1,4
х 2,1
h1
D2
D1
С5
А5
В5
D4
х4,5
С4
А4
В4
E4
E1
E2
α⁰
С2
А2
В2
С1
А1
В1
х 2,1
f2
f1
11
12
22
21
Δy
Δy
β⁰
ЛНН1
ЛНН2
12
11
6
v
v
Натуральная
величина
А(х,у,z)
B(x,y,z)
C(x,y,z)
06.10.2021
Лекция 3