Содержание
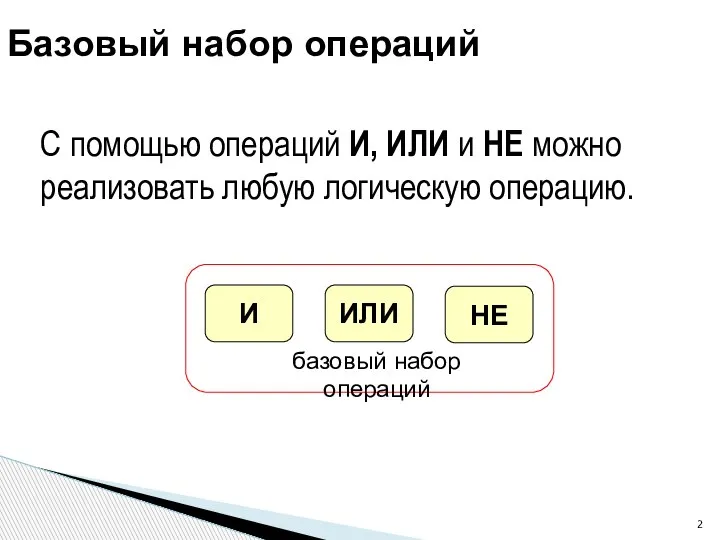
- 2. Базовый набор операций С помощью операций И, ИЛИ и НЕ можно реализовать любую логическую операцию.
- 3. Цифровой сигнал – это сигнал, который может принимать только одно из двух установленных значений. Принято: появление
- 4. Преобразователь, который, получая сигналы об истинности отдельных высказываний, обрабатывает их и в результате выдаёт значение логического
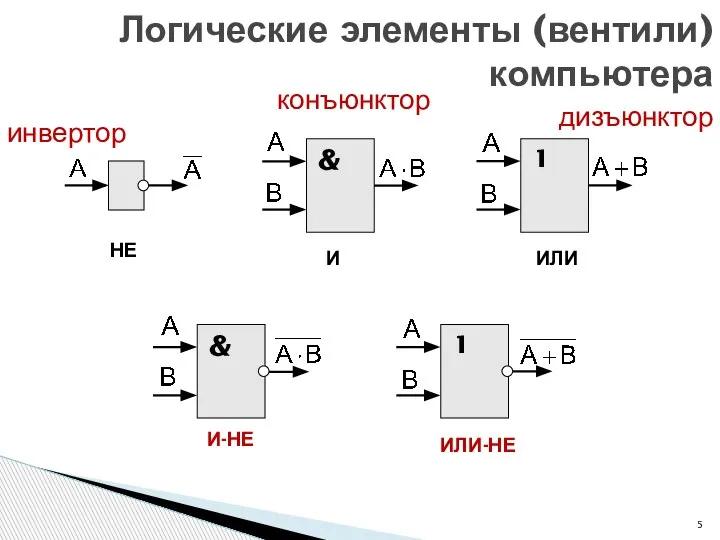
- 5. Логические элементы (вентили) компьютера НЕ И ИЛИ ИЛИ-НЕ И-НЕ инвертор конъюнктор дизъюнктор
- 6. С помощью логических элементов НЕ, И, ИЛИ можно реализовать (собрать как из конструктора) типовые функциональные узлы
- 7. Цепочка из логических элементов, в которой выходы одних элементов являются входами других, называют логическим устройством. Схема
- 8. Чтобы понять, как работает интересующее нас устройство, необходимо понять логику его работы, т.е. найти соответствие между
- 9. Правило построения логических схем: определить число логических переменных; определить количество базовых логических операций и их порядок;
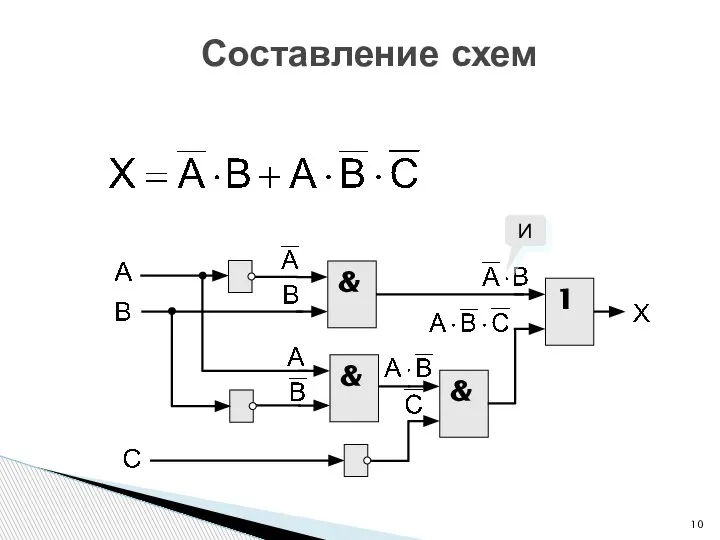
- 10. Составление схем & И
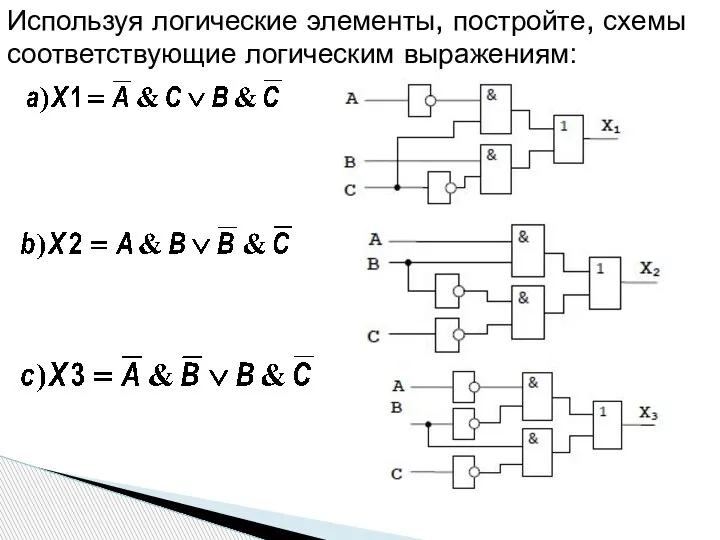
- 11. Используя логические элементы, постройте, схемы соответствующие логическим выражениям:
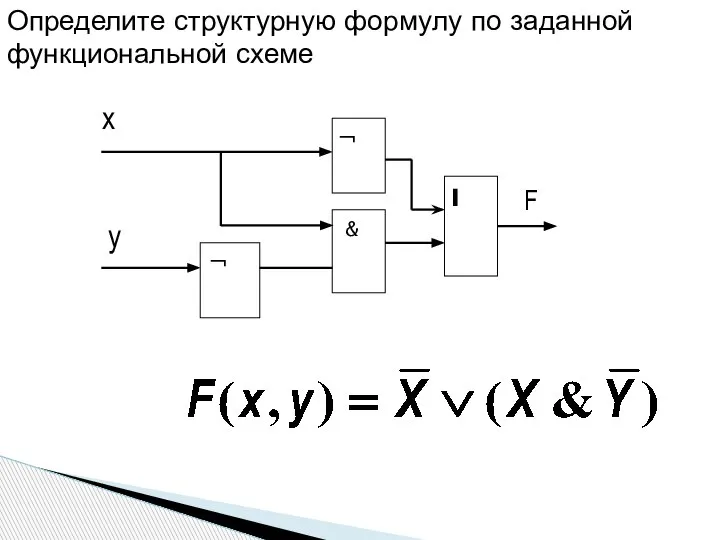
- 12. Определите структурную формулу по заданной функциональной схеме
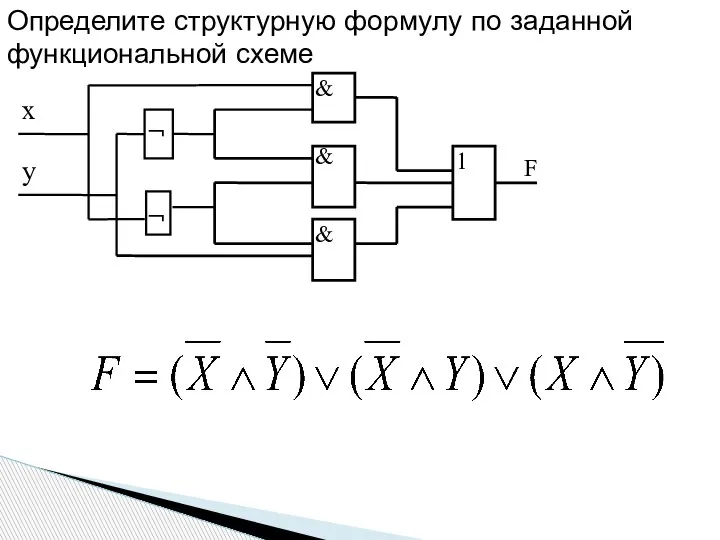
- 13. Определите структурную формулу по заданной функциональной схеме
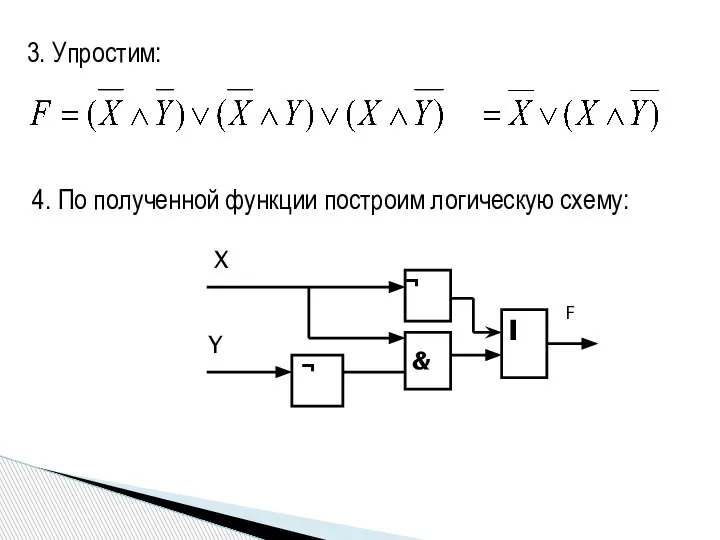
- 14. По заданной таблице истинности записать логическую функцию, упростить ее и построить логическую схему. 1. Запишем конъюнкцию
- 15. 4. По полученной функции построим логическую схему: 3. Упростим:
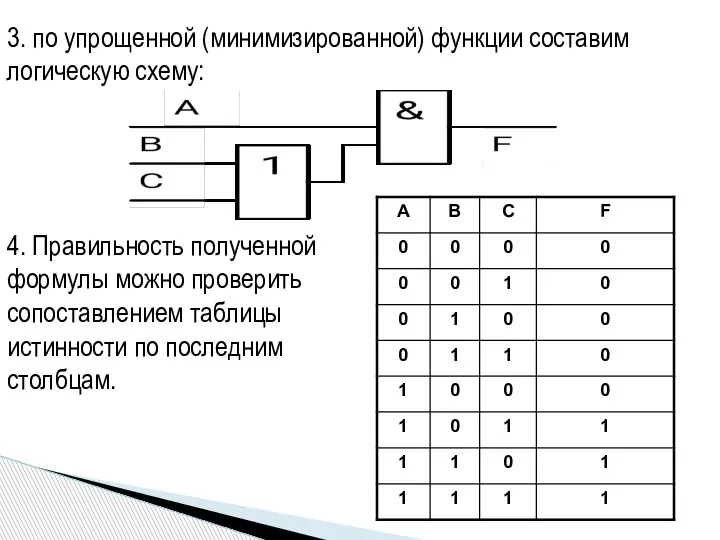
- 16. Составить схему, работа которой задана таблицей истинности: 1. Составим логическую формулу схемы: 2. Упростим полученную формулу:
- 17. 3. по упрощенной (минимизированной) функции составим логическую схему: 4. Правильность полученной формулы можно проверить сопоставлением таблицы
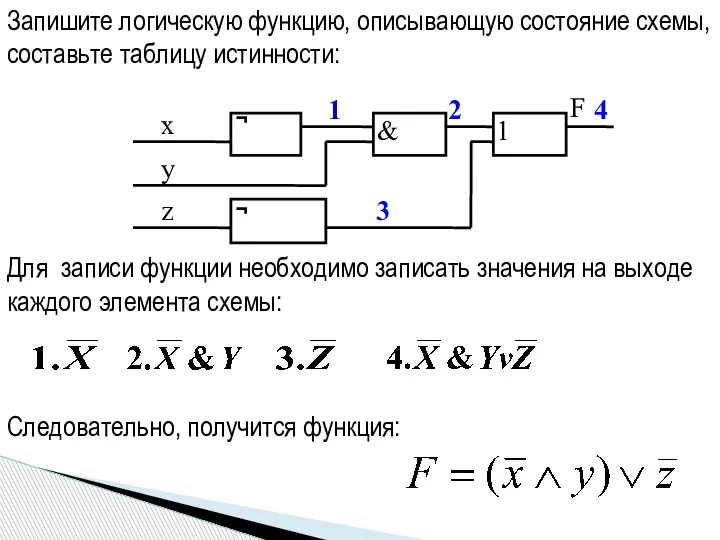
- 18. Запишите логическую функцию, описывающую состояние схемы, составьте таблицу истинности: Для записи функции необходимо записать значения на
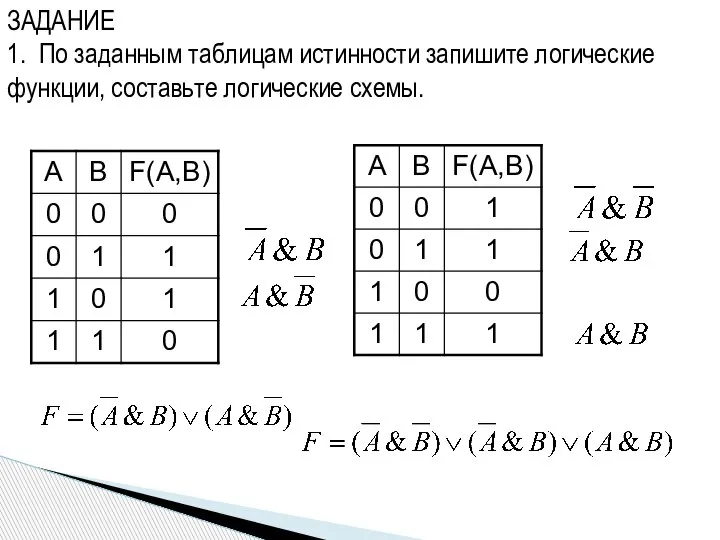
- 19. ЗАДАНИЕ 1. По заданным таблицам истинности запишите логические функции, составьте логические схемы.
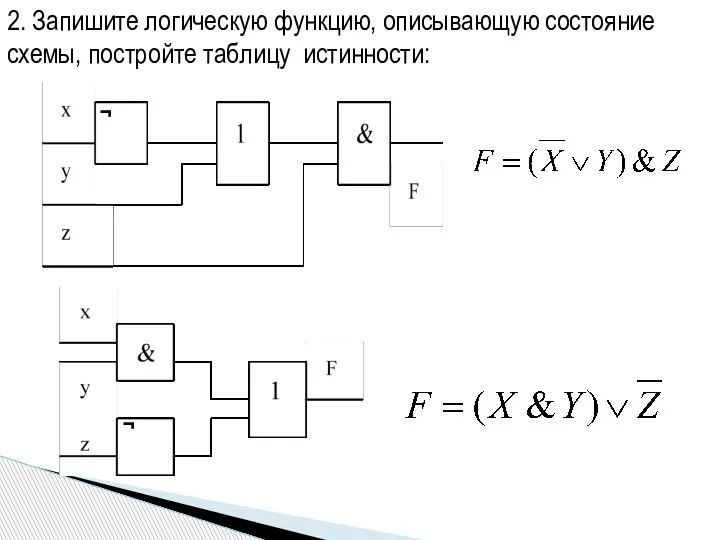
- 20. 2. Запишите логическую функцию, описывающую состояние схемы, постройте таблицу истинности:
- 21. 3. Упростите:
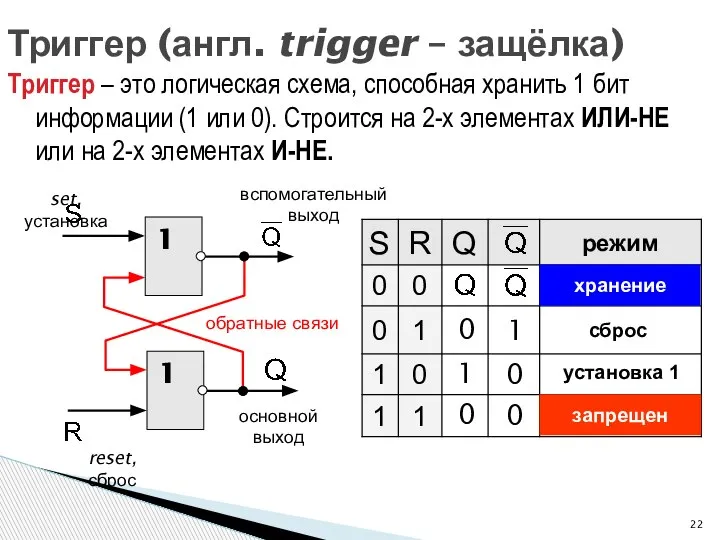
- 22. Триггер (англ. trigger – защёлка) Триггер – это логическая схема, способная хранить 1 бит информации (1
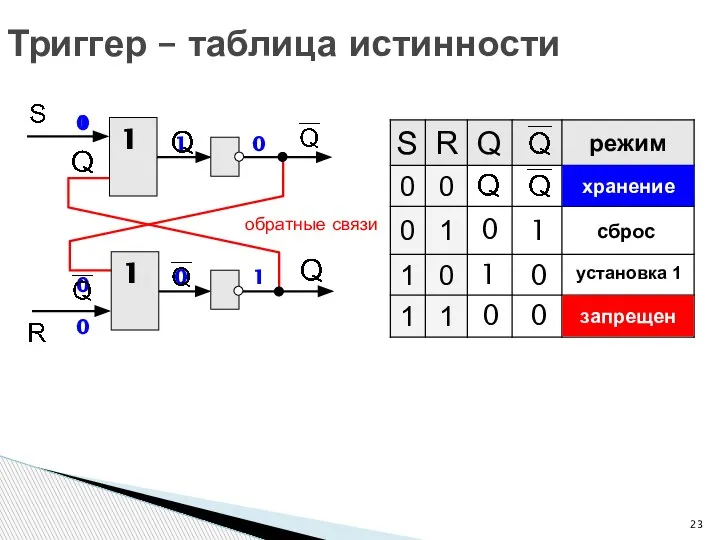
- 23. Триггер – таблица истинности 1 1 обратные связи 1 1 0 0 0 0 1 0
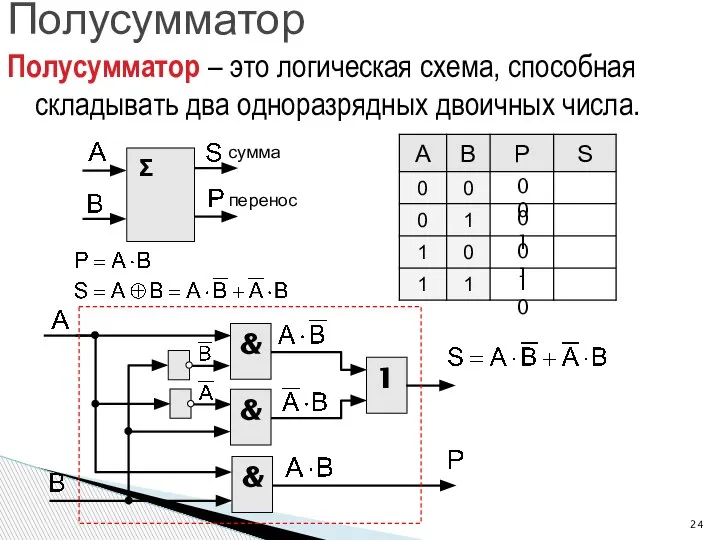
- 24. Полусумматор Полусумматор – это логическая схема, способная складывать два одноразрядных двоичных числа. 0 0 0 1
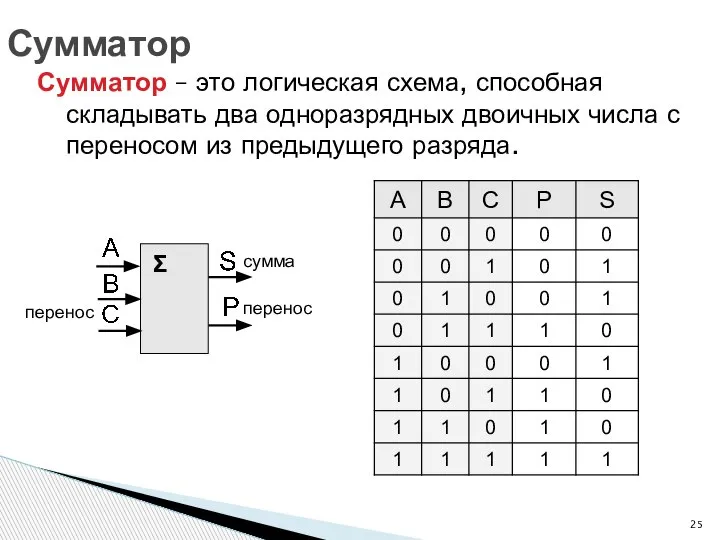
- 25. Сумматор Сумматор – это логическая схема, способная складывать два одноразрядных двоичных числа с переносом из предыдущего
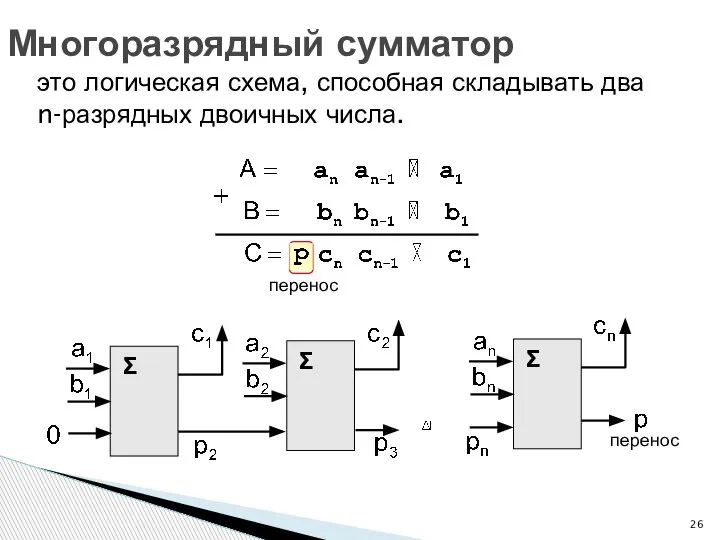
- 26. Многоразрядный сумматор это логическая схема, способная складывать два n-разрядных двоичных числа. перенос перенос
- 28. Скачать презентацию









 Хранение информации
Хранение информации Использование возможностей текстового редактора MS WORD при оформлении документов
Использование возможностей текстового редактора MS WORD при оформлении документов Программа Ехсеl: создание таблиц
Программа Ехсеl: создание таблиц Управление стейкхолдерами проекта. Антивирусы
Управление стейкхолдерами проекта. Антивирусы Графический редактор Paint
Графический редактор Paint Всемирная сеть интернет. Обобщающий урок
Всемирная сеть интернет. Обобщающий урок Файлы и файловая система
Файлы и файловая система AVadm1-1 (2)
AVadm1-1 (2) Разработка музыкального сайта
Разработка музыкального сайта Офисные технологии
Офисные технологии Структурное программирование
Структурное программирование Автоматизированное рабочее место. Структура АРМ. Техническое и программное
Автоматизированное рабочее место. Структура АРМ. Техническое и программное Slides on lists. Operation on lists
Slides on lists. Operation on lists Лонгрид. Мультимедийные элементы
Лонгрид. Мультимедийные элементы Информатика. Повторение изученного. Безопасное поведение
Информатика. Повторение изученного. Безопасное поведение Основы научных исследований. Представление научного доклада в форме презентации. Тема 9
Основы научных исследований. Представление научного доклада в форме презентации. Тема 9 Оформление библиографического описания
Оформление библиографического описания Анализ электронных таблиц и диаграмм
Анализ электронных таблиц и диаграмм Проверка закономерностей методом рассуждений. Тренировочный тест для подготовки к ЕГЭ по информатике
Проверка закономерностей методом рассуждений. Тренировочный тест для подготовки к ЕГЭ по информатике Единицы измерения информации
Единицы измерения информации Компьютерная грамотность
Компьютерная грамотность Объекты окружающего мира
Объекты окружающего мира Администрирование информационных систем. Подключение ис к узлу оператора связи
Администрирование информационных систем. Подключение ис к узлу оператора связи Веб-лаболотория - WPS Office
Веб-лаболотория - WPS Office 6204
6204 Кладовка smm-щика
Кладовка smm-щика VII областной конкурс компьютерного творчества и исследовательских проектов Цифровая палитра
VII областной конкурс компьютерного творчества и исследовательских проектов Цифровая палитра Лекция 7_Технические каналы утечки акустической информации
Лекция 7_Технические каналы утечки акустической информации