Фильтрация изображений

Содержание
Фильтрация
Линейные фильтры
Сглаживающие фильтры
Шумоподавление при помощи прямоугольного фильтра
Гауссовский фильтр
Контрастоповышающие фильтры
Разностные фильтры
Лапласиан
Нелинейные фильтры
Морфологические операторы

Фильтрация
Правила, задающие фильтрацию (их называют фильтрами ), могут быть самыми разнообразными.
Фильтрация изображений является одной из самых фундаментальных операций компьютерного зрения, распознавания образов и обработки изображений.
Фактически, с той или иной фильтрации исходных изображений начинается работа подавляющего большинства методов.
Фильтры имеют, таким образом, чрезвычайную важность с точки зрения их применения в различных приложениях.

Линейные фильтры
Линейные фильтры представляют собой семейство фильтров, имеющих очень простое математическое описание.
Вместе с тем они позволяют добиться самых разнообразных эффектов. Будем считать, что задано исходное полутоновое изображение A, и обозначим интенсивности его пикселей A(x, y).
Линейный фильтр определяется вещественно значной функцией F, заданной на растре.
Данная функция называется ядром фильтра, а сама фильтрация производится при помощи операции дискретной свертки (взвешенного суммирования)
( 1)
Результатом служит изображение B.
Обычно ядро фильтра отлично от нуля только в некоторой окрестности N точки (0, 0). За пределами этой окрестности F(i, j) или в точности равно нулю, или очень близко к нему, так что можно им пренебречь.

Ядро фильтра
Суммирование в (1) производится по i,j , и значение каждого пикселя B(x, y) определяется пикселями изображения A, которые лежат в окне N, центрированном в точке (x, y) (мы будем обозначать это множество N(x, y) ).
Ядро фильтра, заданное на прямоугольной окрестности N, может рассматриваться как матрица m на n, где длины сторон являются нечетными числами. При задании ядра матрицей Mkl, ее следует центрировать:
( 2)
Также нуждается в дополнительном прояснении ситуация, когда пиксель (x, y) находится в окрестности краев изображения. В этом случае A(x + i, y + j) в определении (1) может соответствовать пикселю A, лежащему за пределами изображения A

Данную проблему (в окрестности краев изображения) можно разрешить несколькими способами
Не проводить фильтрацию для таких пикселей, обрезав изображение B по краям или закрасив их, к примеру, черным цветом.
Не включать соответствующий пиксель в суммирование, распределив его вес F(i, j) равномерно среди других пикселей окрестности N(x, y).
Доопределить значения пикселей за границами изображения при помощи экстраполяции. Например, считать постоянным значение интенсивности вблизи границы (для пикселя (-2, 5) имеем A(-2, 5) = A(0, 5) ) или считать постоянным градиент интенсивности вблизи границы ( A(-2, 5) = A(0, 5) + 2(A(0, 5) - A(1, 5)) ).
Доопределить значения пикселей за границами изображения, при помощи зеркального отражения ( A(-2, 5) = A(2, 5) ).
Выбор конкретного способа нужно производить с учетом конкретного фильтра и особенностей конкретного приложения.

Сглаживающие фильтры
Сглаживающие фильтры действуют на изображение аналогично мутному стеклу и: изображение становится нерезким, размытым. Простейший прямоугольный сглаживающий фильтр радиуса r задается при помощи матрицы размера (2r + 1) x (2r + 1), все значения которой равны
а сумма по всем элементам матрицы равна, таким образом, единице. При фильтрации с данным ядром значение пикселя заменяется на усредненное значение пикселей в квадрате со стороной 2r+1 вокруг него.
Пример фильтрации при помощи прямоугольного фильтра приведен на рис. 1.
Рассмотрим особенности сглаживания при помощи прямоугольного фильтра. Характерной чертой этого фильтра, отличающей его, к примеру, от эффекта расфокусировки линз в реальной жизни, является то, что образом белой точки на черном фоне будет равномерно серый квадрат.
Проявления этого эффекта хорошо заметны и на нижнем правом изображении рис. 1: длинные узкие объекты "размазываются" в прямоугольники равномерной интенсивности.

Слева вверху - пример изображения, справа верху- результат фильтрации для r = 1, слева внизу - результат фильтрации для r = 3,справа внизу - результат фильтрации для r = 5.

Для чего сглаживающие фильтры
Одним из их возможных применений является шумоподавление, т.е. задача восстановления исходного изображения, к пикселям которого добавлен случайный шум.
Шум меняется независимо от пикселя к пикселю и, при условии, что математическое ожидание значения шума равно нулю, шумы соседних пикселей будут компенсировать друг друга.
Чем больше окно фильтрации, тем меньше будет усредненная интенсивность шума, однако при этом будет происходить и существенное размытие значащих деталей изображения.

Шумоподавление при помощи прямоугольного фильтра
Естественным предположением об исходном незашумленном изображении будет схожесть значений интенсивности пикселей, находящихся рядом.
Причем чем меньше расстояние между пикселями, тем больше вероятность их похожести.
Это и отличает исходное незашумленное изображение от шумовой компоненты, для которой схожесть пикселей никак не зависит от расстояния между ними.
Исходя из вышесказанного можно предположить, что шумоподавление при помощи прямоугольного фильтра имеет существенный недостаток: пиксели на расстоянии r от обрабатываемого оказывают на результат тот же эффект, что и соседние.

Гауссовский фильтр
Более эффективное шумоподавление можно, таким образом, осуществить, если влияние пикселей друг на друга будет уменьшаться с расстоянием.
Этим свойством обладает гауссовский фильтр с ядром:
( 3)
Гауссовский фильтр имеет ненулевое ядро бесконечного размера.
Однако ядро фильтра очень быстро убывает к нулю при удалении от точки (0, 0), и потому на практике можно ограничиться сверткой с окном небольшого размера вокруг (0, 0) (например, взяв радиус окна равным 3 сигма).

Гауссовская фильтрация
Гауссовская фильтрация также является сглаживающей. Однако, в отличие от прямоугольного фильтра, образом точки при гауссовой фильтрации будет симметричное размытое пятно, с убыванием яркости от середины к краям, что гораздо ближе к реальному размытию от расфокусированных линз.
Как и следовало ожидать, гауссовская фильтрация более эффективна при шумоподавлении (рис. 2): влияние пикселей друг на друга при гауссовой фильтрации обратно пропорционально квадрату расстояния между ними.
Как видно из (3), коэффициент пропорциональности, а следовательно, и степень размытия, определяются параметром сигма.

Контрастоповышающие фильтры
Если сглаживающие фильтры снижают локальную контрастность изображения, размывая его, то контрастоповышающие фильтры производят обратный эффект. Ядро контрастоповышающего фильтра имеет значение, большее 1, в точке (0, 0), при общей сумме всех значений, равной 1. Например, контрастоповышающим фильтром является фильтр с ядром, задаваемым матрицей:
( 4)
или матрицей
( 5)
Эффект повышения контраста достигается за счет того, что фильтр подчеркивает разницу между интенсивностями соседних пикселей, удаляя эти интенсивности друг от друга (рис. 3).
Этот эффект будет тем сильней, чем больше значение центрального члена ядра.
Характерным артефактом линейной контрастоповышающей фильтрации являются заметные светлые и менее заметные темные ореолы вокруг границ.

Рис. 3. Контрастоповышающая фильтрация
На рисунке 3 сверху - исходное изображение. Среднее - эффект от применения фильтра с ядром ,
последнее - эффект от применения фильтра с ядром

Разностные фильтры
Рассмотрим линейные фильтры, задаваемые дискретными аппроксимациями дифференциальных операторов (по методу конечных разностей
Простейшим дифференциальным оператором является взятие производной по x -координате . Данный оператор определен для непрерывных функций.
Существует множество способов определить аналогичный оператор для дискретных изображений при помощи линейного фильтра.
В частности, распространенными вариантами являются фильтры Прюита (Prewitt) и Собеля (Sobel).

Разностные фильтры
Фильтр Прюита задается матрицей
( 6)
Фильтр Собеля задается матрицей
( 7)
Фильтры, приближающие оператор производной по y -координате , получаются путем транспонирования матриц.

Фильтры, находящие границы
В отличии от сглаживающих и контрастоповышающих фильтров, не меняющих среднюю интенсивность изображения (сумма элементов ядра равна единице), в результате применения разностных операторов получается, как правило, изображение со средним значением пикселя близким к нулю (сумма элементов ядра равна нулю).
Вертикальным перепадам (границам) исходного изображения соответствуют пиксели с большими по модулю значениями на результирующем изображении. Поэтому разностные фильтры называют также фильтрами, находящими границы (рис. 4).

Пример
На верхнем рисунке - нахождение производной при помощи фильтра Собеля с ядром , нижний - нахождение производной по у при помощи фильтра Собеля с ядром . Серый цвет соответстует значению 0.

Лапласиан
Аналогично вышеприведенным фильтрам, по методу конечных разностей можно составить фильтры для других дифференциальных операторов.
В частности, важный для многих приложений дифференциальный оператор Лапласа ( лапласиан )
можно приблизить для дискретных изображений фильтром с матрицей (один из вариантов):
( 8)
Как видно на рис. 5, в результате применения дискретного лапласиана большие по модулю значения соответствуют как вертикальным, так и горизонтальным перепадам яркости. является, таким образом, фильтром, находящим границы любой ориентации.
Нахождение границ на изображении может производиться путем применения этого фильтра и взятия всех пикселей, модуль значения которых превосходит некоторый порог.

Задача нахождения границ на изображении является, как мы видим, весьма непростой.
Однако такой алгоритм имеет существенные недостатки.
Главный из них - неопределенность в выборе величины порога.
Для разных частей изображения приемлемый результат обычно получается при существенно разных пороговых значениях.
Кроме того, разностные фильтры очень чувствительны к шумам изображения.

Рис 5

Нелинейные фильтры
Примеры нелинейных фильтров
Линейные фильтры, несмотря на разнообразие производимых ими эффектов, не позволяют проделывать некоторые самые естественные операции. Хорошим примером служит пороговая фильтрация. Результатом пороговой фильтрации служит бинарное изображение, определяемое следующим образом:
( 9)
Величина гамма является порогом фильтрации.
В приложениях используется еще целый ряд простейших нелинейных фильтров. Например, модуль изображения, содержащего пиксели с отрицательным значением, или фильтр, обнуляющий все значения пикселей, меньше данного порога.
Более сложным фильтром, задействующим в вычислениях окрестность пикселя, является медиана. Медианная фильтрация определяется следующим образом:
( 10)
т.е. результат фильтрации есть медианное значение пикселей окрестности1, форма которой выбирается произвольно.

Применение нелинейной фильтрации.
Слева вверху - пример изображения, справа вверху – изображение "загрязнено" большим количеством "битых" черных и белых пикселей, внизу слева - результат нелинейной медианной фильтрации с окрестностью 3 x 3 пикселя, внизу справа – для сравнения, результат применения линейного прямоугольного фильтра с той же окрестностью.

Медианная фильтрация
способна эффективно справляться с помехами в более общем случае, когда помехи независимо воздействуют на отдельные пиксели.
Например, такими помехами являются "битые" и "горячие" пиксели при цифровой съемке, "снеговой" шум, когда часть пикселей заменяется на пиксели с максимальной интенсивностью, и т.п.
Преимущество медианной фильтрации перед линейной сглаживающей фильтрацией заключается в том, что "горячий" пиксель на темном фоне будет заменен на темный, а не "размазан" по окрестности

Фильтры минимум и максимум
которые определяются по правилам
( 11)
( 12)
т.е. результат фильтрации есть минимальное и максимальное значения пикселей окрестности.
Данные фильтры, как правило, применяются для бинарных изображений.
В применении к бинарным изображениям, минимум и максимум, а также еще несколько составных фильтров, построенных на их основе, называются морфологическими операторами

Морфологические операторы
Морфологические операторы суть фильтры, применяемые для морфологического анализа бинарных изображений.
В морфологическом анализе бинарное изображение рассматривается как вид задания формы двумерной геометрической фигуры (пиксели, равные 1, считаются лежащими внутри фигуры, а равные 0 - вовне).
Морфологический анализ активно применяется в таких приложениях, как векторизация изображений, оптическое распознавание символов и другие задачи распознавания образов.

Сужающие и расширяющие фильтры
Базовыми морфологическими операторами являются, фильтры минимум и максимум.
В результате их применения форма, задаваемая изображением, сужается и, соответственно, расширяется (рис. 7), поэтому в морфологическом анализе данные фильтры называют сужающим и расширяющим.
Окрестность пикселя (x, y), фигурирующая в определении (11), для морфологических операторов называется структурным элементом.
Часто применяемыми составными морфологическими операторами являются открывающий и замыкающий фильтры.
Первый состоит в последовательном применении сужающего и расширяющего операторов с одинаковым структурным элементом.
Его морфологический эффект заключается в удалении малых изолированных частей фигуры.
Применение сначала расширяющего, а затем сужающего оператора дает замыкающий фильтр.
Его эффект заключается в заполнении малых изолированных дырок фигуры.
В обоих случаях, "малость" объекта определяется размером и формой структурного элемента операторов.

Рис 7
А б
В г д

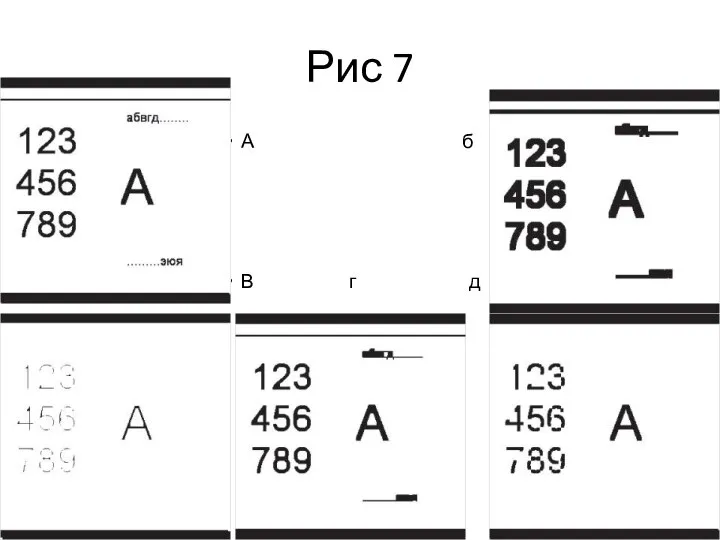
Рис. 7. Применение морфологических операторов.
Структурный элемент - квадратная окрестность 5x5.
а - исходное изображение,
б - сужающий фильтр,
в - расширяющий фильтр,
г - открывающий фильтр,
д - замыкающий фильтр