Содержание
- 2. Логические основы компьютеров § 18. Логика и компьютер
- 3. Логика, высказывания Логика (др.греч. λογικος) – это наука о том, как правильно рассуждать, делать выводы, доказывать
- 4. Высказывание или нет? Сейчас идет дождь. Жирафы летят на север. История – интересный предмет. У квадрата
- 5. Логика и компьютер Двоичное кодирование – все виды информации кодируются с помощью 0 и 1. Задача
- 6. Логические основы компьютеров § 19. Логические операции
- 7. Обозначение высказываний A – Сейчас идет дождь. B – Форточка открыта. простые высказывания (элементарные) Составные высказывания
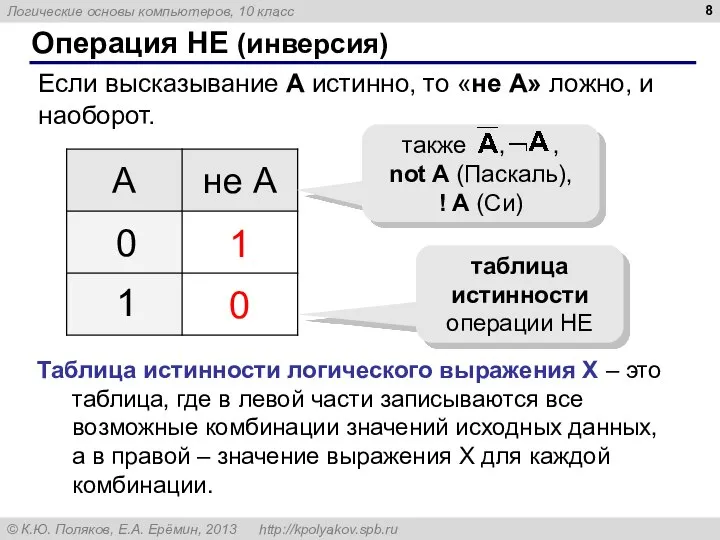
- 8. Операция НЕ (инверсия) Если высказывание A истинно, то «не А» ложно, и наоборот. 1 0 0
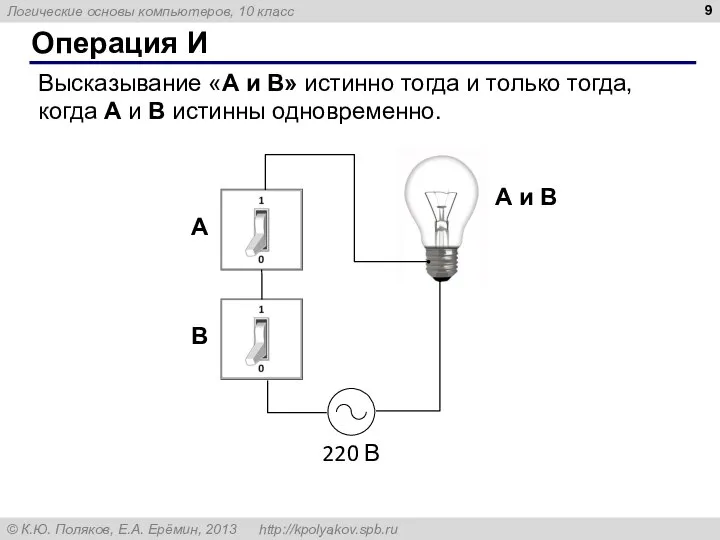
- 9. Операция И Высказывание «A и B» истинно тогда и только тогда, когда А и B истинны
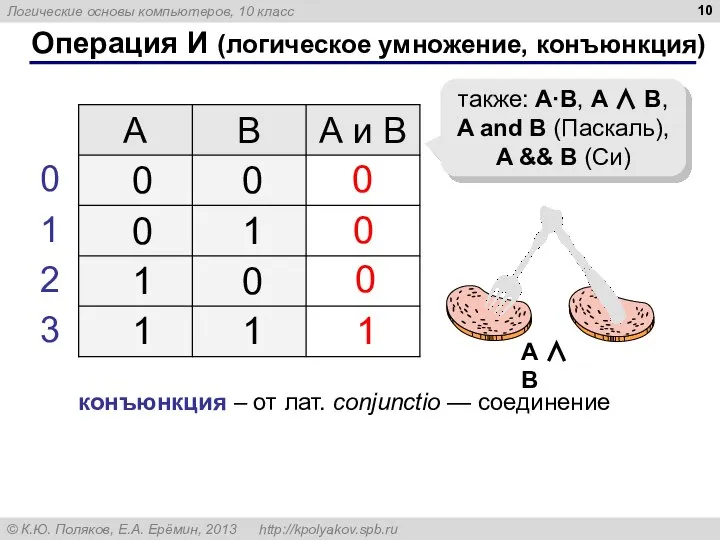
- 10. Операция И (логическое умножение, конъюнкция) 1 0 также: A·B, A ∧ B, A and B (Паскаль),
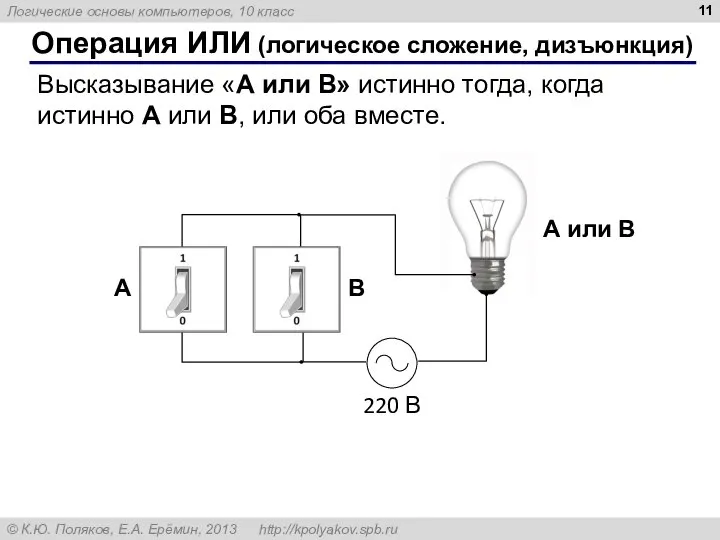
- 11. Операция ИЛИ (логическое сложение, дизъюнкция) Высказывание «A или B» истинно тогда, когда истинно А или B,
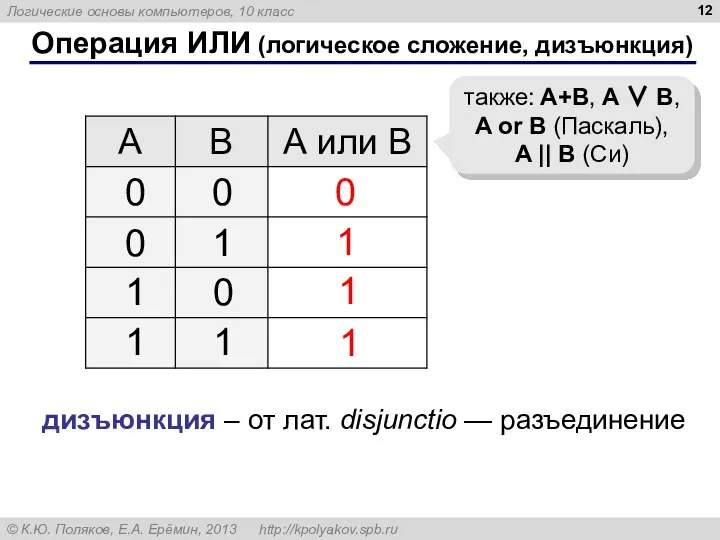
- 12. Операция ИЛИ (логическое сложение, дизъюнкция) 1 0 также: A+B, A ∨ B, A or B (Паскаль),
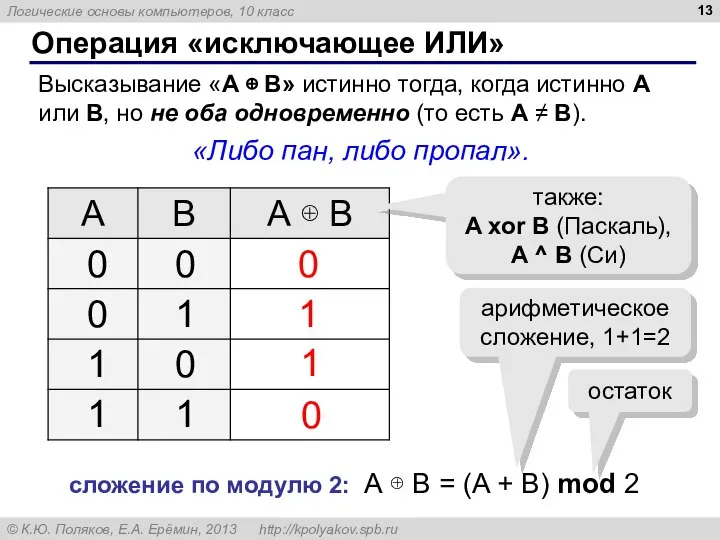
- 13. Операция «исключающее ИЛИ» Высказывание «A ⊕ B» истинно тогда, когда истинно А или B, но не
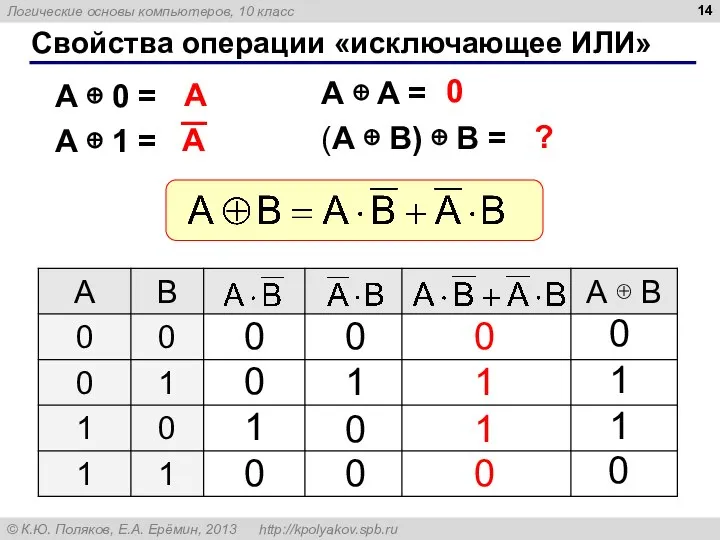
- 14. Свойства операции «исключающее ИЛИ» A ⊕ A = (A ⊕ B) ⊕ B = A ⊕
- 15. Импликация («если …, то …») Высказывание «A → B» истинно, если не исключено, что из А
- 16. Импликация («если …, то …») «Если Вася идет гулять, то Маша сидит дома». A – «Вася
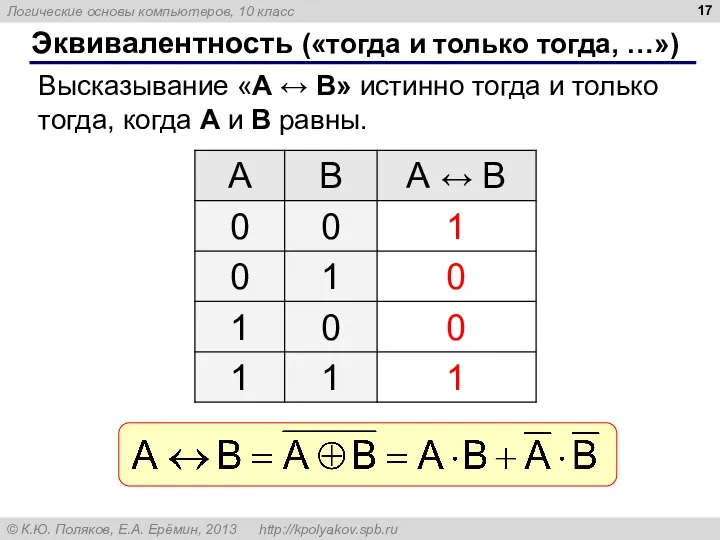
- 17. Эквивалентность («тогда и только тогда, …») Высказывание «A ↔ B» истинно тогда и только тогда, когда
- 18. Базовый набор операций С помощью операций И, ИЛИ и НЕ можно реализовать любую логическую операцию.
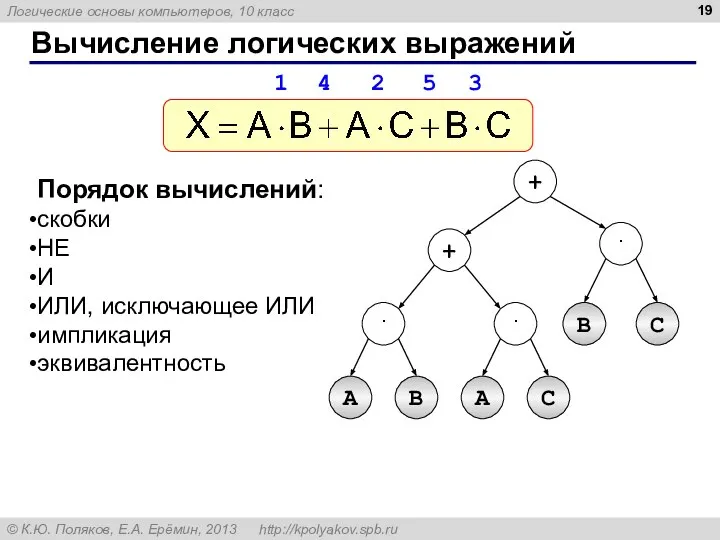
- 19. Вычисление логических выражений Порядок вычислений: скобки НЕ И ИЛИ, исключающее ИЛИ импликация эквивалентность A B +
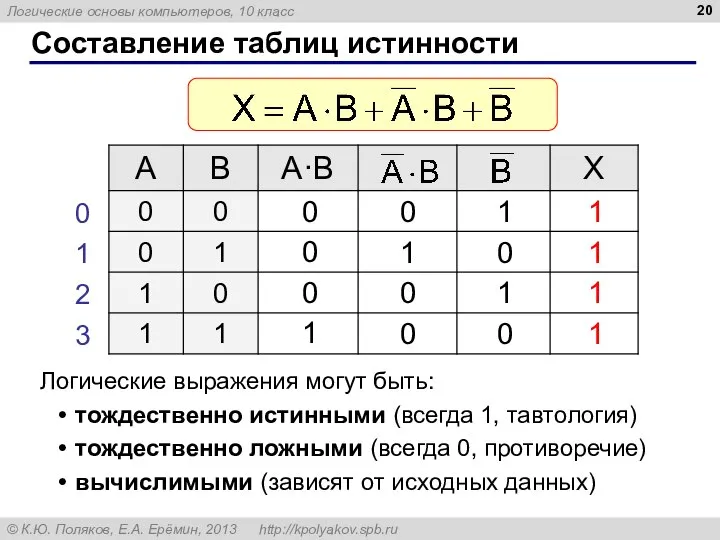
- 20. Составление таблиц истинности Логические выражения могут быть: тождественно истинными (всегда 1, тавтология) тождественно ложными (всегда 0,
- 21. Составление таблиц истинности
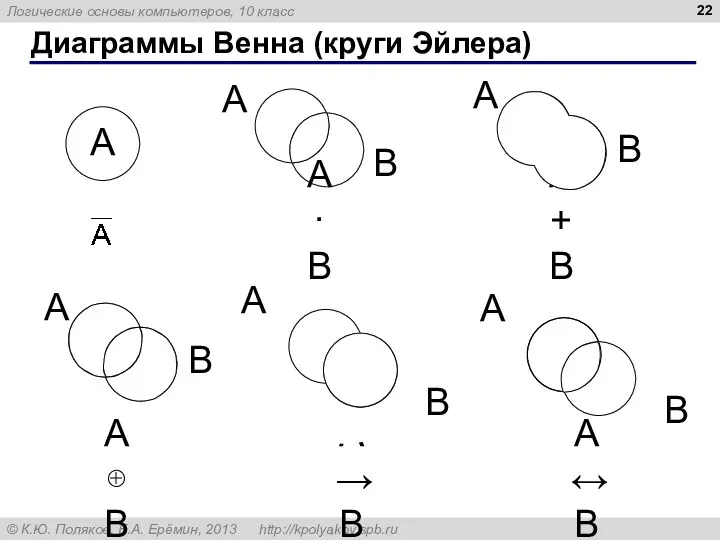
- 22. Диаграммы Венна (круги Эйлера) A·B A+B A⊕B A→B A↔B
- 23. Упрощение логических выражений Шаг 1. Заменить операции ⊕→↔ на их выражения через И, ИЛИ и НЕ:
- 24. Упрощение логических выражений раскрыли → формула де Моргана распределительный исключения третьего повторения поглощения
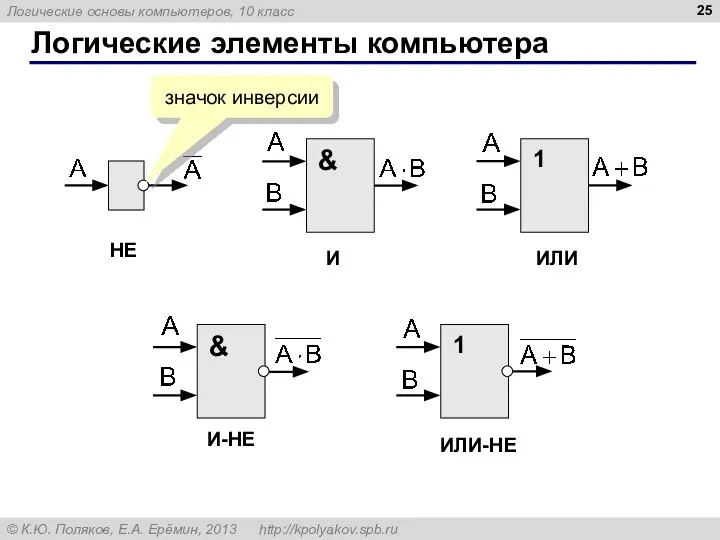
- 25. Логические элементы компьютера НЕ И ИЛИ ИЛИ-НЕ И-НЕ значок инверсии
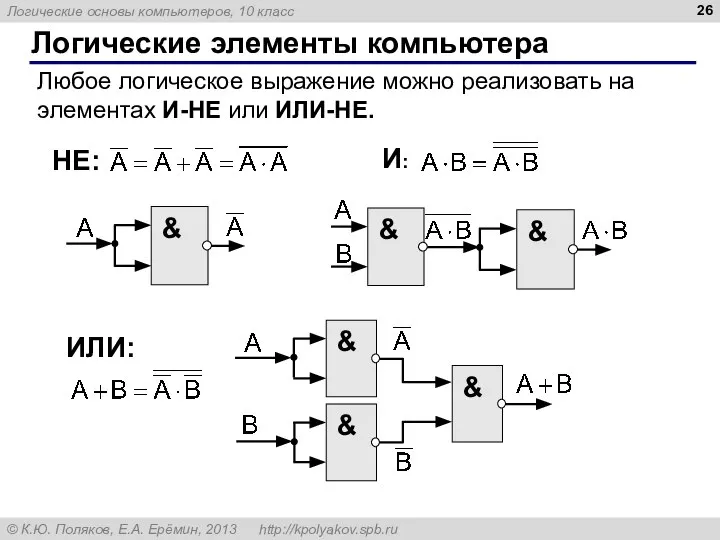
- 26. Логические элементы компьютера Любое логическое выражение можно реализовать на элементах И-НЕ или ИЛИ-НЕ. И: НЕ: ИЛИ:
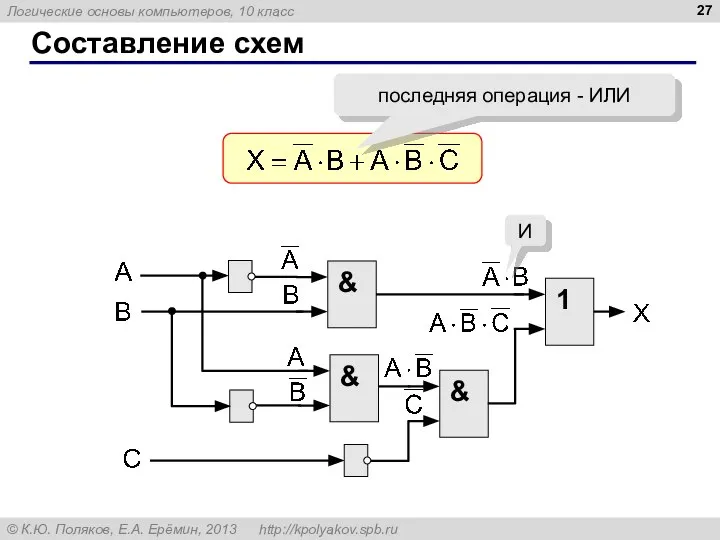
- 27. Составление схем последняя операция - ИЛИ & И
- 28. Конец фильма ПОЛЯКОВ Константин Юрьевич д.т.н., учитель информатики ГБОУ СОШ № 163, г. Санкт-Петербург [email protected] ЕРЕМИН
- 30. Скачать презентацию












 Библиотека в социальных сетях
Библиотека в социальных сетях Основные термины модели в системе трёхмерного моделирования. Компас – 3D
Основные термины модели в системе трёхмерного моделирования. Компас – 3D Библиографическая запись. Библиографическое описание
Библиографическая запись. Библиографическое описание Настольные издательские системы
Настольные издательские системы SIS: A system for Personal Information Retrieval and Re-Use
SIS: A system for Personal Information Retrieval and Re-Use ФСБУ 5. Ответы на вопросы
ФСБУ 5. Ответы на вопросы Машинно-зависимые языки программирования. Лекция 4
Машинно-зависимые языки программирования. Лекция 4 Использование систем мгновенного обмена сообщениями в процессе иноязычной подготовки студентов на примере сервиса Discord
Использование систем мгновенного обмена сообщениями в процессе иноязычной подготовки студентов на примере сервиса Discord Презентация №2 - CSS
Презентация №2 - CSS BestProger. Изучайте программирование без лишней информации
BestProger. Изучайте программирование без лишней информации Киберспорт
Киберспорт Интернет-браузеры
Интернет-браузеры Энигма. Устройство
Энигма. Устройство Разбор задач ЕГЭ. Оператор присваивания и ветвления. В2
Разбор задач ЕГЭ. Оператор присваивания и ветвления. В2 Форматы команд процессора. (Лекция 19.2)
Форматы команд процессора. (Лекция 19.2) Нарративные стратегии в журналистике
Нарративные стратегии в журналистике Техника шрифтовых работ в художественном оформлении. Приемы работы ширококонечным пером
Техника шрифтовых работ в художественном оформлении. Приемы работы ширококонечным пером Інформація. Інформаційні процеси
Інформація. Інформаційні процеси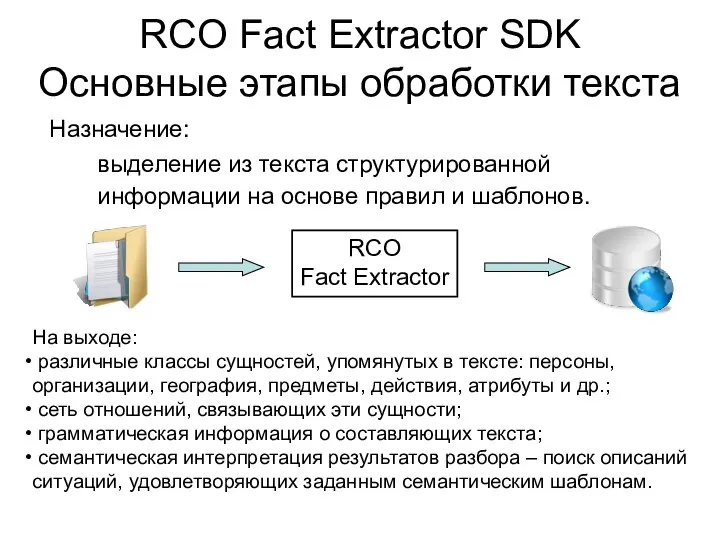 RCO Fact Exctractor SDK - Основные этапы обработки текста
RCO Fact Exctractor SDK - Основные этапы обработки текста Основы языка HTML. Язык разметки гипертекста
Основы языка HTML. Язык разметки гипертекста Правовое обеспечение информационной безопасности. Лекция №6. Правовое обеспечение информационной безопасности
Правовое обеспечение информационной безопасности. Лекция №6. Правовое обеспечение информационной безопасности Компплектующие Компьютера
Компплектующие Компьютера Вибiр та формування сигналiв в цифрових трактах
Вибiр та формування сигналiв в цифрових трактах Измерение информации
Измерение информации Реализация на жесткой и программируемой логике
Реализация на жесткой и программируемой логике Основы работы в OrCad
Основы работы в OrCad Прикладные методы расчета надёжности компьютерных систем и комплексов по логическим схемам
Прикладные методы расчета надёжности компьютерных систем и комплексов по логическим схемам ИнфоБелГУ: Учебный процесс НИУ БелГУ
ИнфоБелГУ: Учебный процесс НИУ БелГУ