Содержание
- 2. Алгебра логики Джордж Буль Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа
- 3. Что же такое логическое высказывание? Логическое высказывание — это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно
- 4. Употребляемые в обычной речи слова и словосочетания "не", "и", "или", "если... , то", "тогда и только
- 5. Bысказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются
- 6. Чтобы обращаться к логическим высказываниям, им назначают имена. Пусть через А обозначено высказывание «2-четное число", а
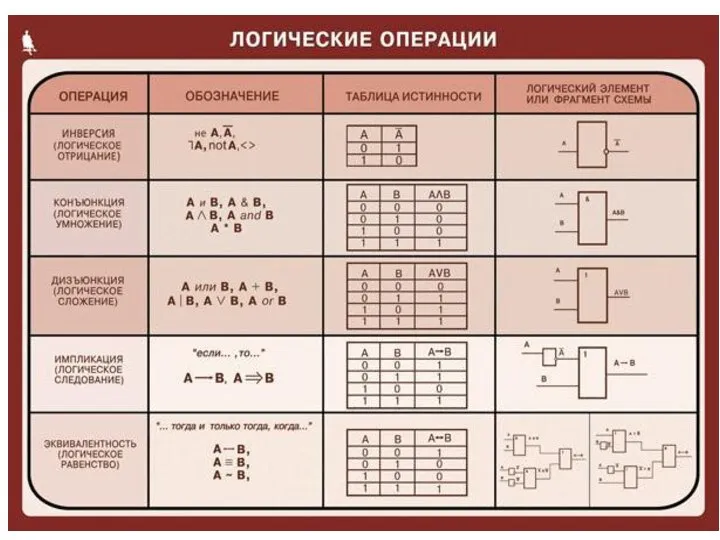
- 7. Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение: конъюнкция,
- 8. Конъюнкция логическое умножение Конъюнкцией высказываний А и В называется высказывание, которое истинно только тогда, когда A
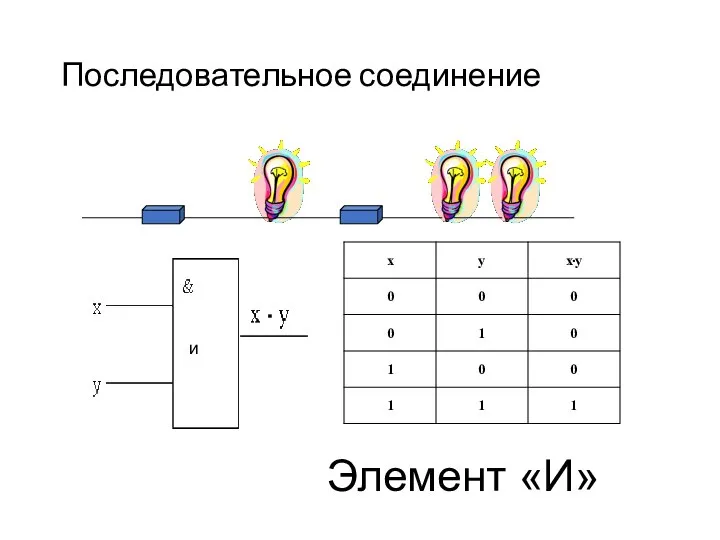
- 9. Последовательное соединение Элемент «И»
- 10. Дизъюнкция Логическое сложение Дизъюнкцией высказываний А и В называется высказывание, которое ложно тогда и только тогда,
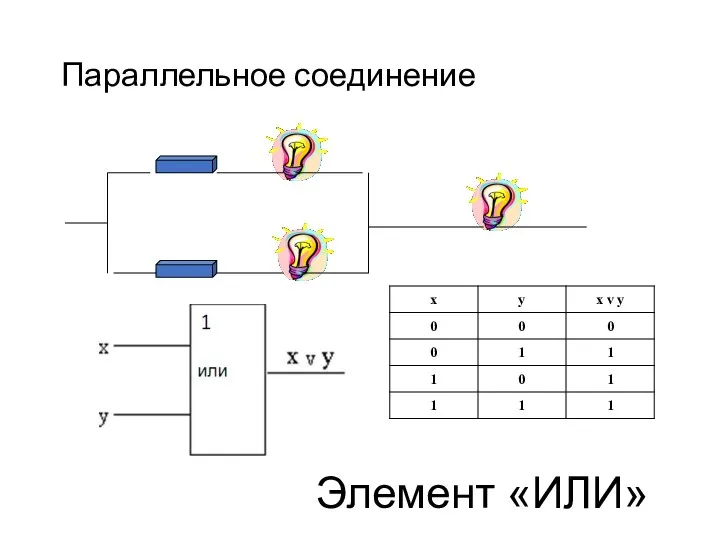
- 11. Параллельное соединение Элемент «ИЛИ»
- 12. Инверсия-Отрицание Отрицанием высказывания А называется высказывание , которое истинно, когда А ложно. Записывается: ; А’ Читается:
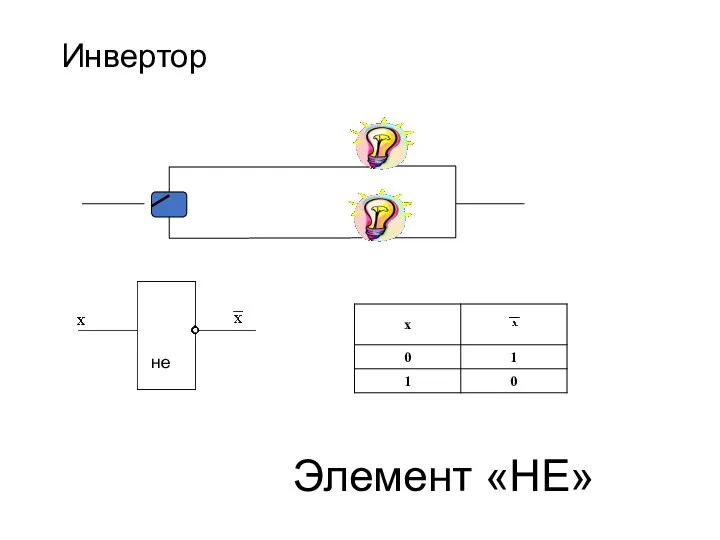
- 13. Инвертор Элемент «НЕ»
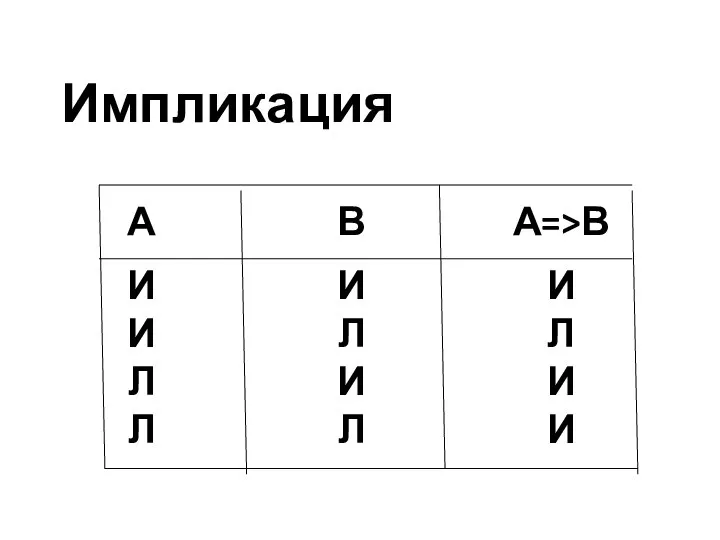
- 14. Импликация Импликацией высказываний А и В называется высказывание, которое ложно тогда и только тогда, когда А
- 15. Импликация
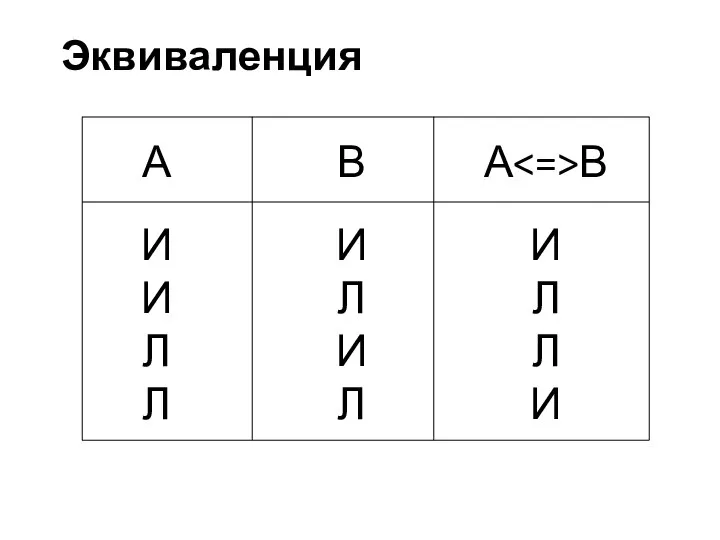
- 16. Эквиваленция Эквиваленцией высказываний А и В называется высказывание, которое истинно тогда и только тогда, когда высказывания
- 17. Эквиваленция
- 18. Последовательность выполне- ния операций в сложных высказываниях задается круглыми скобками. Но для уменьшения числа скобок договорились
- 19. Логическая формула. С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть
- 20. Таблица истинности это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности
- 21. Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре: (0, 0), (0, 1),
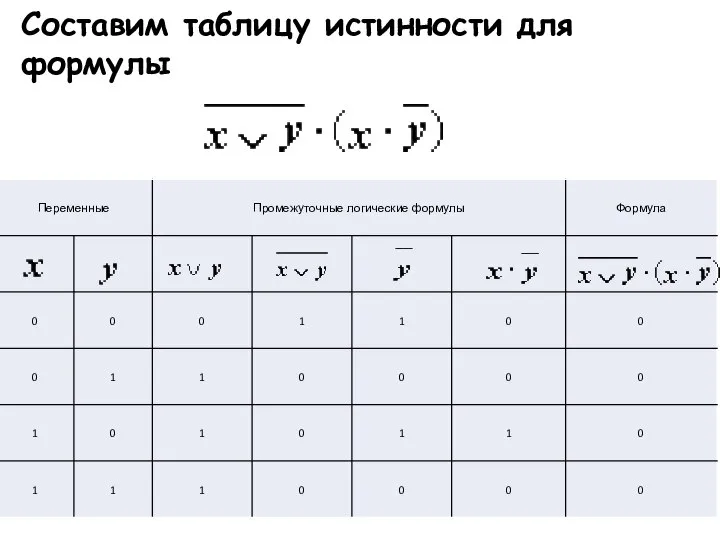
- 22. Составим таблицу истинности для формулы
- 23. Если при всех наборах значений переменных x и y формула принимает значение 1, то она является
- 26. Рассмотрим особенности Записи целых чисел со знаком на примере однобайтового формата, при котором для знака отводится
- 27. В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код,
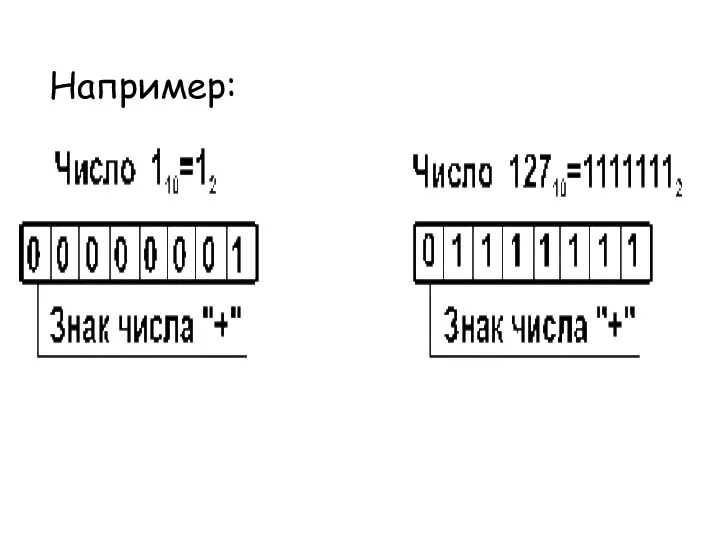
- 28. Например:
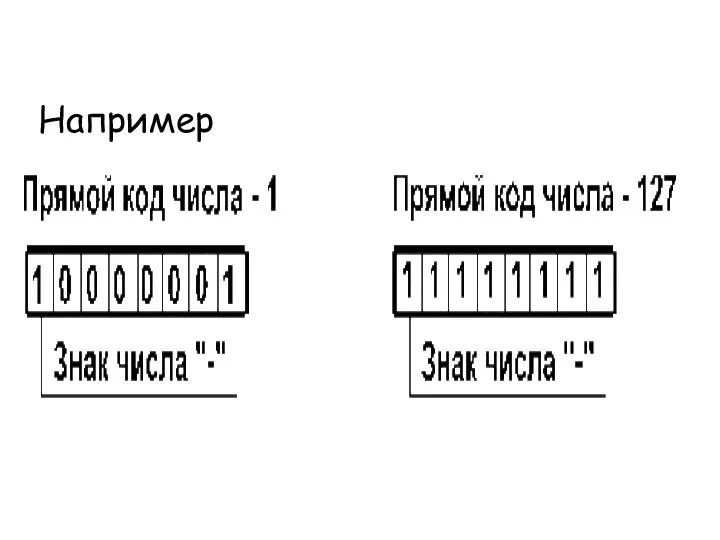
- 29. Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа — двоичный
- 30. Например
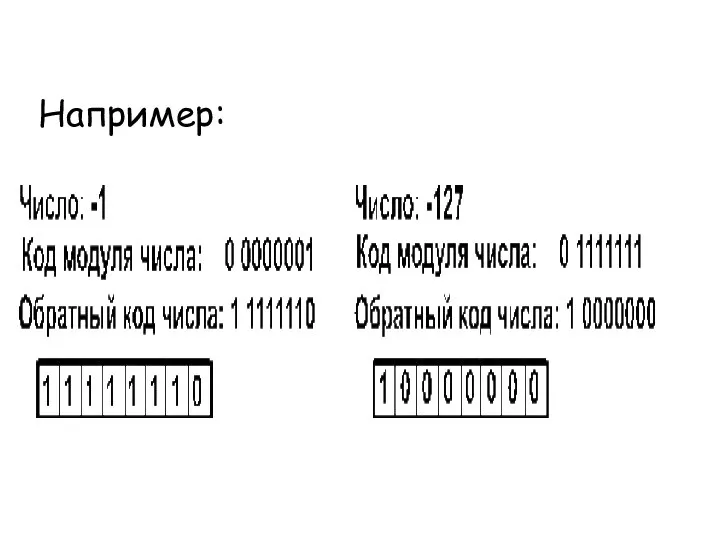
- 31. * Обратный код. Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули
- 32. Например:
- 34. Скачать презентацию





















 Tekhnologii_ERP
Tekhnologii_ERP Платформа Freescale Semiconductor для реализации беспроводных решений ZigBee / 802.15.4 / SMAC
Платформа Freescale Semiconductor для реализации беспроводных решений ZigBee / 802.15.4 / SMAC Системы телемедицины. Программное обеспечение для телемедицины. Лекция 4
Системы телемедицины. Программное обеспечение для телемедицины. Лекция 4 Основы программирования на языке C++
Основы программирования на языке C++ Какво представлява WebAssembly
Какво представлява WebAssembly Введення повідомлення 05 про склад поїзда
Введення повідомлення 05 про склад поїзда лекция 5
лекция 5 Сэмюэл Морзе – телеграф и код Морзе
Сэмюэл Морзе – телеграф и код Морзе Информация, сообщения
Информация, сообщения Programing C
Programing C Задача о потоке минимальной стоимости
Задача о потоке минимальной стоимости Программирование циклов
Программирование циклов Презентация на тему Электронные деньги
Презентация на тему Электронные деньги  Коммерческое предложение по составлению SEO-стратегии
Коммерческое предложение по составлению SEO-стратегии Система управления базами данных моделирование и формализация. 9 класс
Система управления базами данных моделирование и формализация. 9 класс Концепция развития сервисного обслуживания предприятий Машиностроительного комплекса
Концепция развития сервисного обслуживания предприятий Машиностроительного комплекса ЭБС Букап
ЭБС Букап Алгоритмы и исполнители. Основы алгоритмизации
Алгоритмы и исполнители. Основы алгоритмизации Формирование информационной грамотности через работу с текстом на уроках окружающего мира
Формирование информационной грамотности через работу с текстом на уроках окружающего мира Устройство анализа сетевого трафика ЦПС
Устройство анализа сетевого трафика ЦПС Просмотр и редактирование жесткого диска (DiskEditor)
Просмотр и редактирование жесткого диска (DiskEditor) Технологии мультимедиа и восприятие ощущений. Общая физиология зрения
Технологии мультимедиа и восприятие ощущений. Общая физиология зрения Использование социальных сетей в деятельности педагога
Использование социальных сетей в деятельности педагога Презентация на тему Создание WEB–сайта с помощью языка HTML
Презентация на тему Создание WEB–сайта с помощью языка HTML  Правила расположения рук на клавиатуре
Правила расположения рук на клавиатуре Вредоносные ПО
Вредоносные ПО Определение каскадной точки входа
Определение каскадной точки входа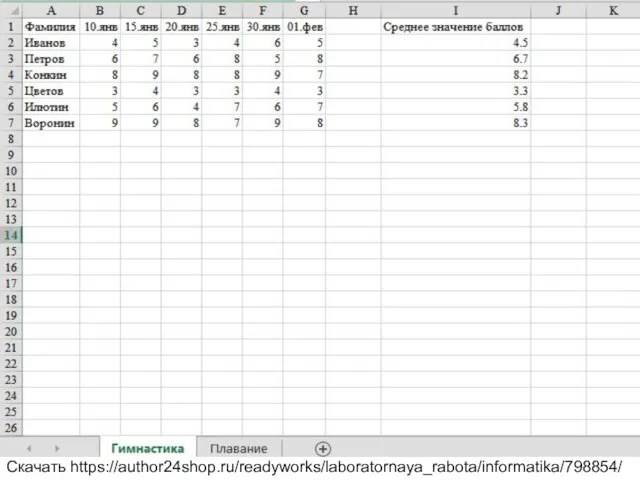 Связь между листами. Лабораторная работа
Связь между листами. Лабораторная работа