Слайд 2РЕШЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. ГЕОМЕТРИЧЕСКИЙ МЕТОД
Графоаналитический (графический) способ решения задач линейного программирования

обычно используется для решения задач с двумя переменными, когда ограничения выражены неравенствами, а также задач, которые могут быть сведены к таким задачам.
Слайд 3ПОРЯДОК ГРАФИЧЕСКОГО РЕШЕНИЯ
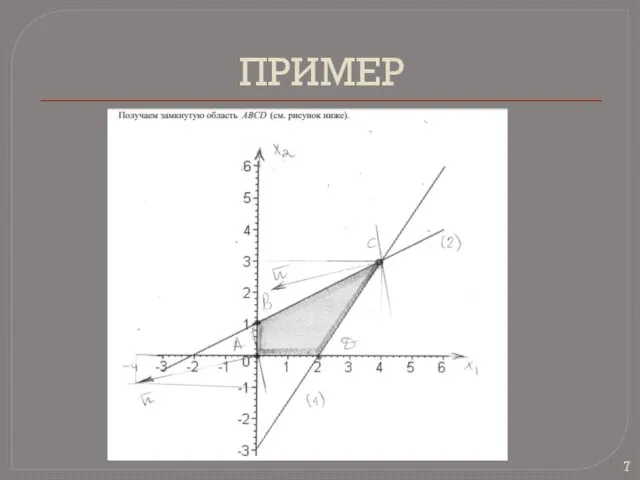
С учетом системы ограничений строится область допустимых решений.
Строится

вектор .
Проводится произвольная линия, перпендикулярная к вектору .
При решении задачи на максимум перемещается линия уровня в направлении вектора так, чтобы она касалась области допустимых решений в ее крайнем положении.
В случае задачи на минимум линия уровня перемещается в антиградиентном направлении.
Определяется оптимальный план и экстремальное значение целевой функции
Слайд 9СИМПЛЕКС МЕТОД
Симплекс метод - это метод последовательного перехода от одного базисного решения (вершины

многогранника решений) системы ограничений задачи линейного программирования к другому базисному решению до тех пор, пока функция цели не примет оптимального значения (максимума или минимума).
Слайд 10Алгоритм симплекс метода
Шаг 1. Привести задачу линейного программирования к канонической форме. Для

этого перенести свободные члены в правые части (если среди этих свободных членов окажутся отрицательные, то соответствующее уравнение или неравенство умножить на - 1) и в каждое ограничение ввести дополнительные переменные (со знаком "плюс", если в исходном неравенстве знак "меньше или равно", и со знаком "минус", если "больше или равно").
Шаг 2. Если в полученной системе m уравнений, то m переменных принять за основные, выразить основные переменные через неосновные и найти соответствующее базисное решение. Если найденное базисное решение окажется допустимым, перейти к допустимому базисному решению.
Шаг 3. Выразить функцию цели через неосновные переменные допустимого базисного решения. Если отыскивается максимум (минимум) линейной формы и в её выражении нет неосновных переменных с отрицательными (положительными) коэффициентами, то критерий оптимальности выполнен и полученное базисное решение является оптимальным - решение окончено. Если при нахождении максимума (минимума) линейной формы в её выражении имеется одна или несколько неосновных переменных с отрицательными (положительными) коэффициентами, перейти к новому базисному решению.
Шаг 4. Из неосновных переменных, входящих в линейную форму с отрицательными (положительными) коэффициентами, выбирают ту, которой соответствует наибольший (по модулю) коэффициент, и переводят её в основные. Переход к шагу 2.
Слайд 17ТРАНСПОРТНАЯ ЗАДАЧА
Задача Монжа - Канторовича - математическая задача линейного программирования специального вида

о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение. Для простоты понимания рассматривается как задача об оптимальном плане перевозок грузов из пунктов отправления (например, складов) в пункты потребления (например, магазины), с минимальными общими затратами на перевозки.
Слайд 18АЛГОРИТМ РЕШЕНИЯ ТРАНСПОРТНОЙ ЗАДАЧИ
Построение транспортной таблицы.
Проверка задачи на закрытость.
Составление опорного плана.
Проверка

опорного плана на вырожденность.
Вычисление потенциалов для плана перевозки.
Проверка опорного плана на оптимальность.
Перераспределение поставок.
Если оптимальноерешение найдено, переходим к п. 9, если нет – к п. 5.
Вычисление общих затрат на перевозку груза.
Построение графа перевозок.
Слайд 27ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Динамическое программирование – подход, позволяющий решать задачи оптимизации, которые могут быть

сформулированы как задачи многошагового оптимального управления некоторой системой.
Слайд 28Элементы модели динамического программирования
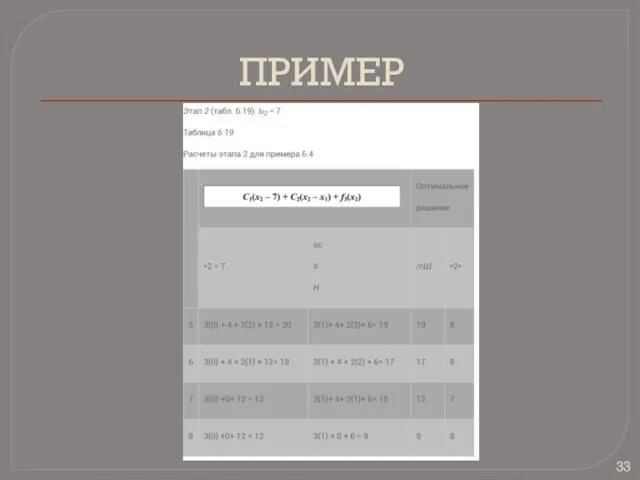
Этап i представляется порядковым номером недели i, i= 1, 2,..., п.
Вариантами решения на i-м этапе

являются значения - количество работающих на протяжении i-й недели.
Состоянием на i-м этапе является *м - количество работающих на протяжении (i - 1)-й недели (этапа).
































 Инкасс
Инкасс Особенности проектов по разработке программного обеспечения
Особенности проектов по разработке программного обеспечения Игра Сетикет
Игра Сетикет Презентация на защиту проекта
Презентация на защиту проекта Среда программирования OpenMP. (Лекция 1)
Среда программирования OpenMP. (Лекция 1) ВКонтакте - российская социальная сеть
ВКонтакте - российская социальная сеть Работа с подсистемой Обращение в Росреестр
Работа с подсистемой Обращение в Росреестр На каких трех китах держится информатика? Логика, алгоритмы и программа
На каких трех китах держится информатика? Логика, алгоритмы и программа Элементы теории множеств
Элементы теории множеств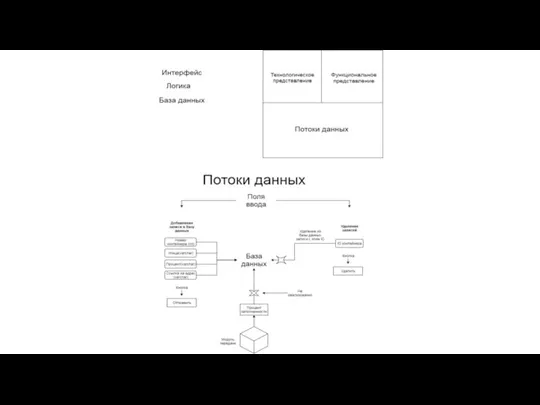 Потоки данных
Потоки данных Дополнительный_материал_17.14_28.09.2022_204006c3 (4)
Дополнительный_материал_17.14_28.09.2022_204006c3 (4) Информационное обеспечение систем управления. Лабораторные работы. Раздел 5
Информационное обеспечение систем управления. Лабораторные работы. Раздел 5 Как составить интелект-карту
Как составить интелект-карту Типы данных в C#
Типы данных в C# Презентация на тему История развития вычислительных средств
Презентация на тему История развития вычислительных средств  Сын Потапа. Рresentation csgo operation
Сын Потапа. Рresentation csgo operation The increasing use of computers has negative effects
The increasing use of computers has negative effects Служба WWW
Служба WWW Программирование на языке Паскаль
Программирование на языке Паскаль Антипаттерны: хардкодинг, софткодинг
Антипаттерны: хардкодинг, софткодинг Мир информатики
Мир информатики 1С:Биллинг. Решение для автоматизации абонентского отдела на предприятиях в сфере услуг
1С:Биллинг. Решение для автоматизации абонентского отдела на предприятиях в сфере услуг Макет мобильного приложения с возможностями дополненной реальности
Макет мобильного приложения с возможностями дополненной реальности Оценка Интернет сайта Департамента экономического развития Брянской области
Оценка Интернет сайта Департамента экономического развития Брянской области Система интервального регулирования Анаконда
Система интервального регулирования Анаконда Жизненный цикл программного обеспечения. Лекция №3
Жизненный цикл программного обеспечения. Лекция №3 Дерево систем и его роль при управлении техническими системами
Дерево систем и его роль при управлении техническими системами Скины 187-го легиона
Скины 187-го легиона