+ 8512 – 2128 – 250
Общая идея: количество значащих нулей равно количеству всех знаков в двоичной записи числа (его длине!) минус количество единиц
Решение
// Учитывая, что 250 = 256 – 4 – 2 = 28 – 22 – 21, приведём все числа к степеням двойки:
4512 + 8512 – 2128 – 250 = (22)512 + (23)512 – 2128 – 28 + 22 + 21 =
=21536 + 21024 – 2128 – 28 + 22 + 21=
// старшая степень двойки 21536, значит двоичная запись этого числа содержит 1537 знаков;
// Используя равенство , получаем:
= 21536 + 21024 – 2129 + 2128 – 28 + 22 + 21
1
895
1
+
+
+
120
1
+
=
1018 «1»
1537-1018=519 («0»)
Ответ: 519
© Е.А. Лапина, 2019










 МИФы нашей школы
МИФы нашей школы Презентация на тему Технологии обработки числовых данных
Презентация на тему Технологии обработки числовых данных  Интернет-маркетинговое агентство Smartnet 24. Внедрение Битрикс24.CRM
Интернет-маркетинговое агентство Smartnet 24. Внедрение Битрикс24.CRM L3_CSMA_CD
L3_CSMA_CD Разработка обучающего веб-сайта по корейскому языку
Разработка обучающего веб-сайта по корейскому языку Операционные системы
Операционные системы Проблематика отзывных площадок
Проблематика отзывных площадок Приём заявлений в 1 класс. Алгоритм подачи заявления в электронном виде
Приём заявлений в 1 класс. Алгоритм подачи заявления в электронном виде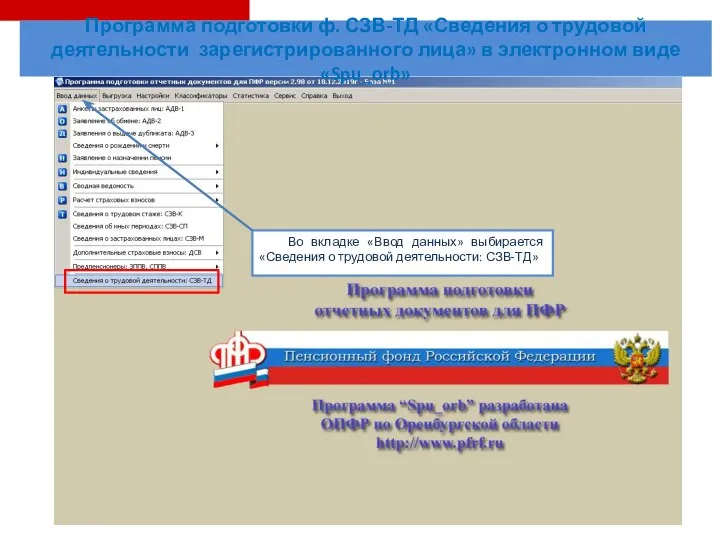 Программа подготовки СЗВ-ТД Сведения о трудовой деятельности зарегистрированного лица в электронном виде Spu_orb
Программа подготовки СЗВ-ТД Сведения о трудовой деятельности зарегистрированного лица в электронном виде Spu_orb SimbirSoft. Сквозной проект. Основы программирования
SimbirSoft. Сквозной проект. Основы программирования Проект Coursera
Проект Coursera СВАН-анализ
СВАН-анализ Файловые менеджеры
Файловые менеджеры Базы данных
Базы данных Создание электронных тестов
Создание электронных тестов Программное обеспечение компьютера
Программное обеспечение компьютера Искусственные и естественные источники информации
Искусственные и естественные источники информации Математическое программное обеспечение автоматизированных систем управления
Математическое программное обеспечение автоматизированных систем управления Моушен дизайн
Моушен дизайн Мессенджер Telegram: портрет пользователей
Мессенджер Telegram: портрет пользователей SQL. Structured Query Language. Структурированный язык запросов
SQL. Structured Query Language. Структурированный язык запросов Оптимизация Photoshop
Оптимизация Photoshop Презентация на тему Компьютеры и здоровье: анализ совместимости
Презентация на тему Компьютеры и здоровье: анализ совместимости  Средства автоматизации проектирования автоматизированных систем
Средства автоматизации проектирования автоматизированных систем Использование цифрового образовательного портала 5 , для реализации парциальной программы Предшкола нового поколения
Использование цифрового образовательного портала 5 , для реализации парциальной программы Предшкола нового поколения Чек-лист полезных ссылок для поиска работы
Чек-лист полезных ссылок для поиска работы Компьютерные сети, классификация
Компьютерные сети, классификация Способы поиска в интернете
Способы поиска в интернете