Минимальное остовное дерево. Система непересекающихся множеств. Олимпиадное программирование

Минимальное остовное дерево
Минимальное остовное дерево (мин. остов, англ. Minimum spanning tree) – такое подмножество рёбер в взвешенном ненаправленном графе, что между любой парой вершин существует ровно один простой путь, а суммарный вес рёбер минимален.
4
5
1
2
3
1
2
3
4
1
4
1
3

Алгоритм Прима
Пусть изначально в мин. остов включена одна вершина. Её можно выбрать произвольно.
Далее в мин. остов добавляется ребро с наименьшим весом, исходящее из этой вершины, и вершина, к которой оно ведёт.
Теперь рассматриваются все рёбра, которые соединяют вершины, входящие в мин. остов, с вершинами, которые ещё в него не входят. Из этих рёбер выбирается минимальное и добавляется в мин. остов, как и вершина, к которой оно ведёт.
Предыдущий шаг повторяется, пока существует ребро, удовлетворяющее всем требованиям.

Реализация О(N2)

Алгоритм Краскала
Каждая вершина представляется как отдельное дерево.
Рёбра сортируются в порядке неубывания весов.
Рассматривается каждое ребро.
Если ребро соединяет вершины из разных деревьев, то оно добавляется в минимальный остов, а эти деревья объединяются.
После перебора всех рёбер все вершины окажутся принадлежащими одному дереву, которое будет являться мин. остовом.

Система непересекающихся множеств
Система непересекающихся множеств (СНМ, англ. disjoint-set-union, DSU) – структура данных которая позволяет администрировать множество элементов, разбитое на непересекающиеся подмножества.
При инициализации СНМ все множества (деревья) системы состоят из 1 элемента (вершины), который является представителем (корнем) своего множества.
Также при инициализации предком каждой вершины считается она сама.

СНМ (2)
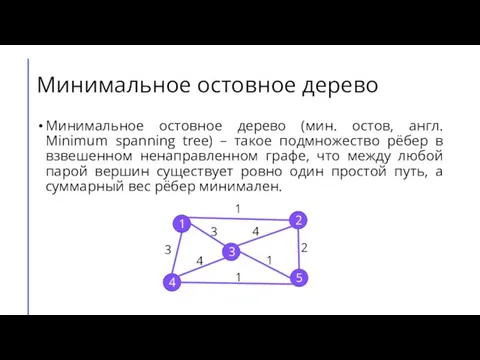
Дерево идентифицируется по своему корню. То есть, чтобы узнать, какому дереву принадлежит вершина, нужно найти корень этого дерева. Если предком вершины является она сама – то она и есть корень. Иначе можно узнать, какому дереву принадлежит предок вершины. Логично, что вершина всегда принадлежит тому же дереву, что её предок, поэтому эта операция уместна. Для предка корень дерева определяется таким же способ, что говорит о рекурсивности данного алгоритма.
Данная реализация определения дерева, которому принадлежит вершина, выполняется за глубину дерева, так как в ней рассматриваются все вершины на пути от заданной до корня. Этот показатель можно улучшить, если после каждой такой операции в качестве предка вершины запоминать найденный корень дерева, которому она принадлежит. Тогда асимптотика этой операции будет O(1).

СНМ (3)
Если корни деревьев, которым принадлежат вершины, различаются, то и деревья являются различными. Если же корни совпадают, то и деревья совпадают.
Объединение деревьев осуществляется путём добавления связи между корнями этих деревьев. При этом корень большего дерева становится предком корня меньшего дерева, к размеру поддерева корня большего дерева добавляется размер поддерева корня меньшего дерева. Такой выбор корня нового дерева обусловлен необходимостью балансировки дерева, чтобы оно не превращалось в «бамбук», что негативно сказывалось бы на времени выполнения операции определения дерева, которому принадлежит вершина.

Реализация СНМ