Содержание
- 2. Модель Ферхюльста. Рост популяции, ограниченный ресурсами Пьер Ферхюльст 1804 - 1849 Ограниченный рост. Зависимость величины скорости
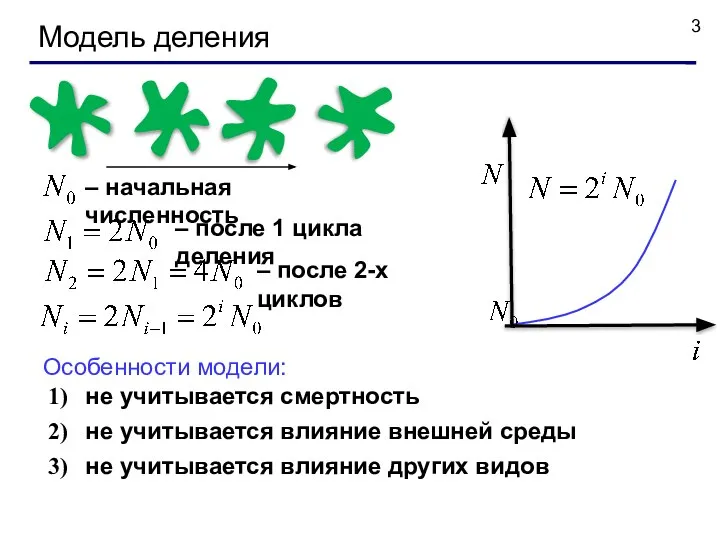
- 3. – начальная численность – после 1 цикла деления – после 2-х циклов Особенности модели: не учитывается
- 4. В(1)- количество больных начальная, В(n) - количество больных через n дней k - коэффициент заражения =
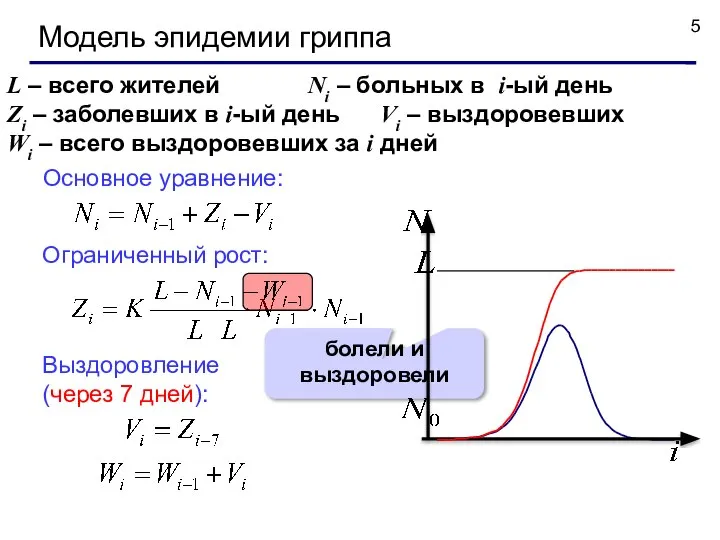
- 5. Модель эпидемии гриппа L – всего жителей Ni – больных в i-ый день Zi – заболевших
- 6. В(1)- количество больных начальная =1, В(n) - количество больных через n дней k - коэффициент заражения
- 7. Математическая модель
- 9. Скачать презентацию




 Теоретические основы информатики. Лекция 1.2
Теоретические основы информатики. Лекция 1.2 Современная библиотека
Современная библиотека Язык программирования Pascal
Язык программирования Pascal MS Office Access
MS Office Access Многопоточность
Многопоточность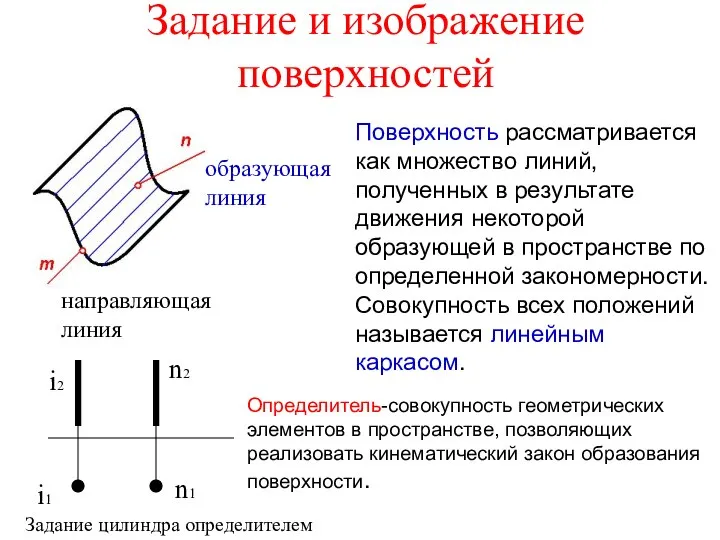 Задание и изображение поверхностей
Задание и изображение поверхностей Объекты(продолжение). Массивы. Деструктуризация
Объекты(продолжение). Массивы. Деструктуризация Анализ трёх обсуждаемых новостей русско-язычного интернета
Анализ трёх обсуждаемых новостей русско-язычного интернета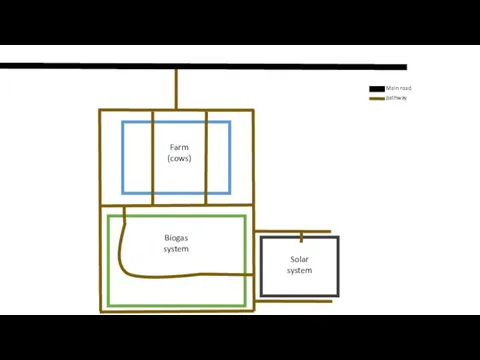 Main road pathway
Main road pathway Функции системы тестирования
Функции системы тестирования 9-1-5
9-1-5 Информационное сообщение объемом
Информационное сообщение объемом Выбор способов построения 3D моделей. (3 занятие)
Выбор способов построения 3D моделей. (3 занятие) Растровые графические редакторы
Растровые графические редакторы Задача и SPARQL-запрос
Задача и SPARQL-запрос Системная динамика
Системная динамика Удобное и быстрое тестирование в школе
Удобное и быстрое тестирование в школе Логические основы компьютера (Тема 3.4.)
Логические основы компьютера (Тема 3.4.) Программирование ветвящихся алгоритмов
Программирование ветвящихся алгоритмов Выпускная квалификационная работа. Технологии набора и верстки журнального разворота с содержанием колонтитула
Выпускная квалификационная работа. Технологии набора и верстки журнального разворота с содержанием колонтитула Способы увеличения эффективности фильтра, напечатанного с применением FDM технологии
Способы увеличения эффективности фильтра, напечатанного с применением FDM технологии Информационно-аналитические технологии: значение для деятельности методических служб общедоступных муниципальных библиотек
Информационно-аналитические технологии: значение для деятельности методических служб общедоступных муниципальных библиотек Область применения многомерного метода анализа данных: кластеризация
Область применения многомерного метода анализа данных: кластеризация Операционная система Windows
Операционная система Windows Практическая работа 1. Знакомство Windows 7
Практическая работа 1. Знакомство Windows 7 Преимущества и порядок перехода на ЭДО. Поставщикам ООО Пивоваренная компания Балтика
Преимущества и порядок перехода на ЭДО. Поставщикам ООО Пивоваренная компания Балтика Диаграмма деятельности
Диаграмма деятельности Сервисы Интернета
Сервисы Интернета