Общие теоретические вопросы. Оптимизация – общая постановка задачи. Целевая функция, система ограничений
Содержание
- 2. Понятие оптимизации Оптимизация - целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях. Постановка задачи
- 3. Выбор компромиссного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи. При постановке задачи
- 4. Модель задачи математического программирования включает: совокупность неизвестных величин, действуя на которые, систему можно совершенствовать. Их называют
- 5. Стандартная математическая задача оптимизации формулируется таким образом:
- 6. ОБЩИЕ ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ Задача линейного программирования. Постановка задачи
- 7. Линейное программирование Линейное программирование — раздел математического программирования, применяемый при разработке методов отыскания экстремума линейных функций
- 8. Постановка задачи
- 9. ОБЩИЕ ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ Графическое решение задачи линейного программирования. Пример
- 10. Пусть дана задача
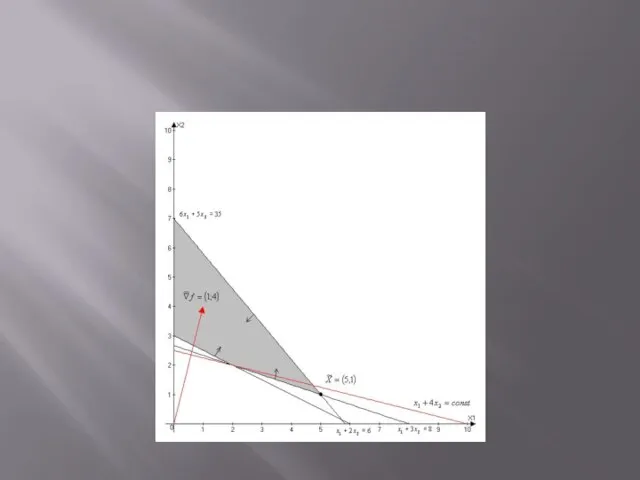
- 11. Геометрическая интерпретация элементов задачи
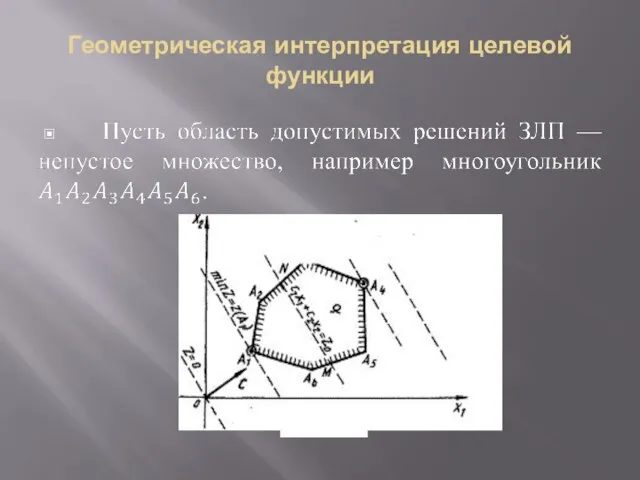
- 12. Геометрическая интерпретация целевой функции
- 15. Порядок решения ЗЛП графическим методом:
- 16. Пример
- 20. РЕШЕНИЕ ПРИКЛАДНЫХ ЗАДАЧ Задача 1
- 21. Дано словесное описание задачи. Привести ее табличное и математическое описание: целевая функция, система ограничений. Завод выпускает
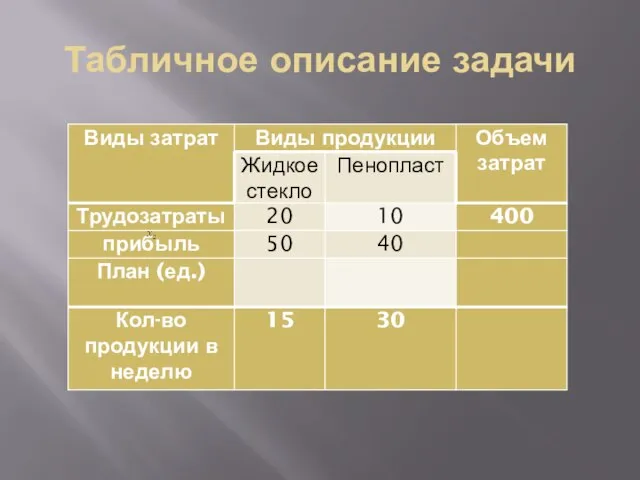
- 22. Табличное описание задачи
- 23. Математическое описание задачи
- 24. РЕШЕНИЕ ПРИКЛАДНЫХ ЗАДАЧ Задача 2
- 25. Дано словесное описание задачи. Привести ее табличное и математическое описание: целевая функция, система ограничений. Предприятие располагает
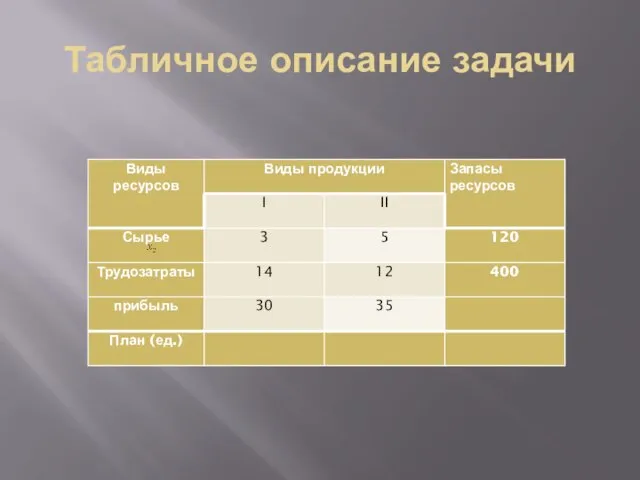
- 26. Табличное описание задачи
- 27. Математическое описание задачи
- 28. РЕШЕНИЕ ПРИКЛАДНЫХ ЗАДАЧ Задача 3
- 29. Дано словесное описание задачи. Привести ее табличное и математическое описание: целевая функция, система ограничений.
- 30. Табличное описание задачи
- 32. Скачать презентацию

























 поиск информации
поиск информации Информатика и информационно-коммуникационные технологии
Информатика и информационно-коммуникационные технологии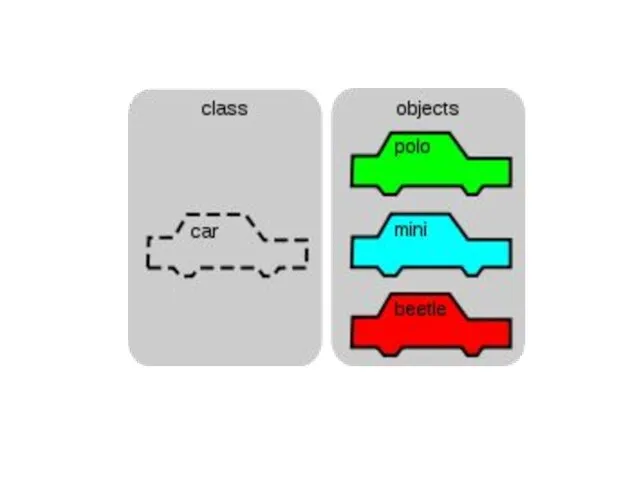 Объектноориентированное программирование. Наследование
Объектноориентированное программирование. Наследование Коммерческое предложение YouTube| октябрь 2016 г
Коммерческое предложение YouTube| октябрь 2016 г 10 лайфхаков, которые немного упростят жизнь во время работы в ворде
10 лайфхаков, которые немного упростят жизнь во время работы в ворде Работа ПФР в социальных медиа. Актуальную информацию для граждан о пенсионной системе
Работа ПФР в социальных медиа. Актуальную информацию для граждан о пенсионной системе ВКР: Использование интернет-технологий в муниципальном образовании для повышения эффективности системы управления
ВКР: Использование интернет-технологий в муниципальном образовании для повышения эффективности системы управления Развитие систем подвижной связи к 5G
Развитие систем подвижной связи к 5G Компьютерное моделирование и 3D прототипирование
Компьютерное моделирование и 3D прототипирование Компьютеры и программы
Компьютеры и программы Зеленый хайп. Что ждет экожурналистов
Зеленый хайп. Что ждет экожурналистов Машинное обучение в управлении БПЛА
Машинное обучение в управлении БПЛА Проектирование информационных систем
Проектирование информационных систем Знаковые модели. Моделирование и формализация
Знаковые модели. Моделирование и формализация HAARP (High Frequency Active Auroral Research Program — программа исследования ионосферного рассеяния высокочастотных радиоволн)
HAARP (High Frequency Active Auroral Research Program — программа исследования ионосферного рассеяния высокочастотных радиоволн) Что такое айтишечка?
Что такое айтишечка? Компьютерная графика
Компьютерная графика algoritmi_sresheniyami
algoritmi_sresheniyami Знакомство с исполнителем Робот
Знакомство с исполнителем Робот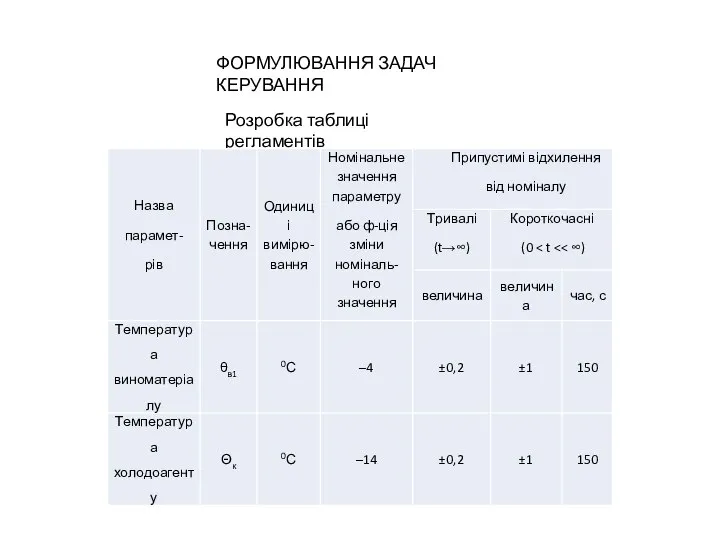 Формулювання задач керування. Розробка таблиці регламентів
Формулювання задач керування. Розробка таблиці регламентів Представление чисел в позиционных системах счисления
Представление чисел в позиционных системах счисления Медиа вызов. Забайкальский государственный университет. Факультет филологии и массовых коммуникаций
Медиа вызов. Забайкальский государственный университет. Факультет филологии и массовых коммуникаций Осторожно, вирусы!
Осторожно, вирусы! Для чего используется моделирование?
Для чего используется моделирование? Как работать с 1с не в локальной сети
Как работать с 1с не в локальной сети Определение скорости передачи информации. Самостоятельная работа. 10 класс
Определение скорости передачи информации. Самостоятельная работа. 10 класс Понятие и система средств массовой коммуникации
Понятие и система средств массовой коммуникации Manual Sops Editor
Manual Sops Editor