Слайд 3Задача
Требуется разложить на простые множители натуральное число с количеством знаков более

11.
Слайд 4План действий
Решение поставленной задачи для «коротких» чисел
Реализация простейших алгебраических операций для «длинных»

чисел
«Сборка» программы и тестирование
Слайд 5Основной алгоритм очевиден.
Несколько «фишек» для
оптимизации программы

Слайд 6Избавляемся от надобности определять простоту числа

Слайд 7Избавляемся от лишних проверок делителей
Рассматриваем делители только до квадратного корня из

данного числа.
Корень вычисляем приблизительно (берем число состоящее из n/2 + 1 девятки, где n – количество цифр в данном числе). Заметим, что этот «корень» наверняка больше, чем его реальное значение, это значит, что делители мы не потеряем.
Слайд 8А вдруг число простое?
Чтобы понять, что введенное число являлось простым и

вывести его единственный простой делитель(само число), определим специальную переменную bool mark = false, значение которой изменим на true, если хотя бы 1 делитель уже был найден. Тогда, после выхода из основного цикла, мы будем знать: было ли число простым.
Слайд 10 Сompleted?..
Нужно еще протестировать…

Слайд 11Тестируем
Посмотрим, как работает защита от типичного (любопытного и шаловливого) пользователя.
Число начинаются

с 0? Нехорошо…
Слайд 12Тестируем
Число начинается с нескольких 0? Еще хуже.
Число содержит какие-то символы,

кроме цифр? Эх… руки бы таким пообрывать…
Слайд 13Тестируем
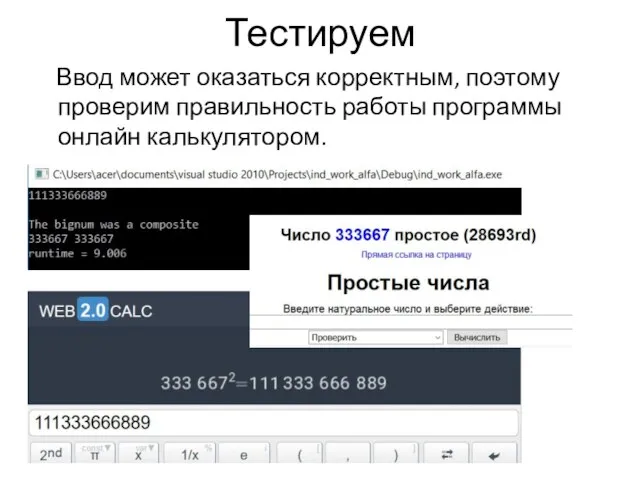
Ввод может оказаться корректным, поэтому проверим правильность работы программы онлайн калькулятором.
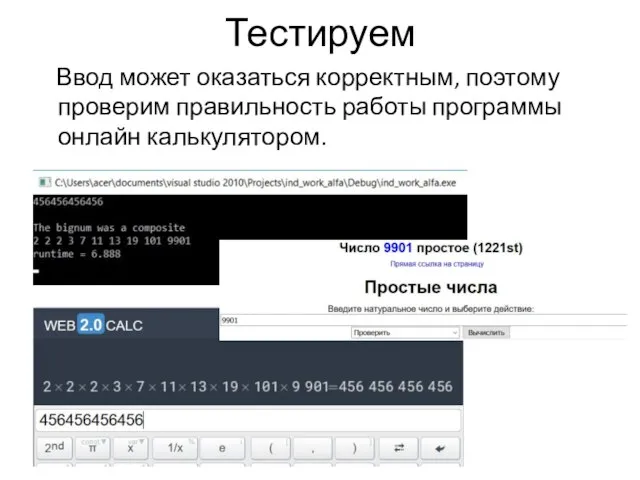
Слайд 14Тестируем
Ввод может оказаться корректным, поэтому проверим правильность работы программы онлайн калькулятором.
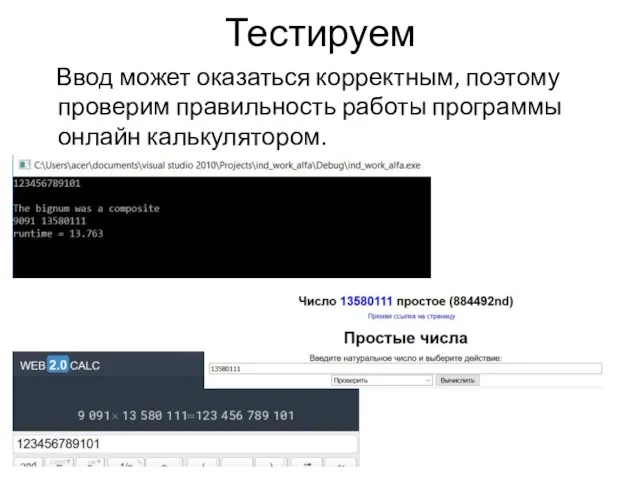
Слайд 15Тестируем
Ввод может оказаться корректным, поэтому проверим правильность работы программы онлайн калькулятором.
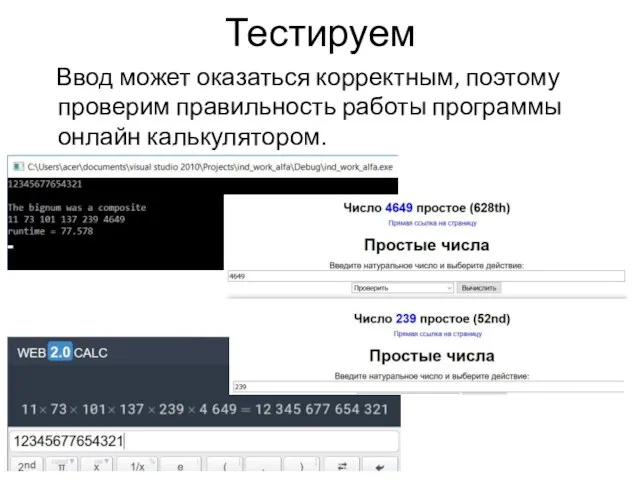
Слайд 16Тестируем
Ввод может оказаться корректным, поэтому проверим правильность работы программы онлайн калькулятором.
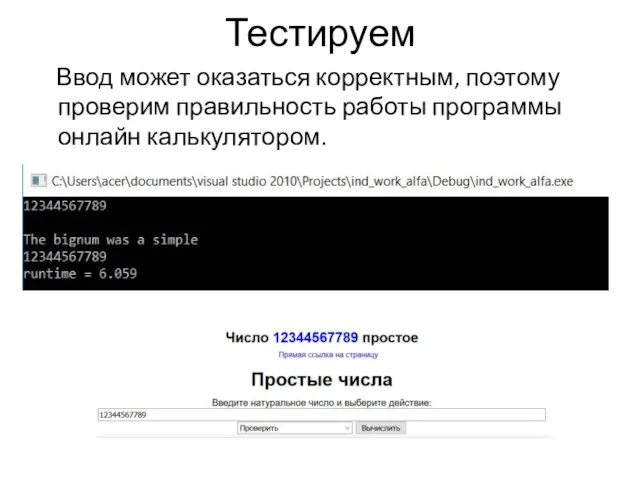
Слайд 17Тестируем
Ввод может оказаться корректным, поэтому проверим правильность работы программы онлайн калькулятором.
Слайд 18Mission complete!
Программа работает. Если брать числа с количеством знаков более 15,

то время выполнения программы будет очень большое.
Какое-то из 16-значных чисел раскладывалось около 54 минут. По роковой случайности (закрыл консоль) screenshot не сохранился.

















 Лекция 6_информатика_ЭТ
Лекция 6_информатика_ЭТ алгоритм рисования треугольника
алгоритм рисования треугольника Коммерческий сайт компании
Коммерческий сайт компании Автоматическая система обнаружения лесных пожаров
Автоматическая система обнаружения лесных пожаров Разбор задач ЕГЭ. Перебор слов и системы счисления. В4
Разбор задач ЕГЭ. Перебор слов и системы счисления. В4 методы коммутации в ткс 17.09 (1)
методы коммутации в ткс 17.09 (1) Как оформить свой Инстаграм и получать клиентов уже сейчас? Только практика
Как оформить свой Инстаграм и получать клиентов уже сейчас? Только практика Игра Сетикет
Игра Сетикет Всемирный день защиты прав потребителей - Цифровой мир: надежные смарт-устройства
Всемирный день защиты прав потребителей - Цифровой мир: надежные смарт-устройства Электронный дневник и конкурс
Электронный дневник и конкурс Архитектура персонального компьютера
Архитектура персонального компьютера Интернет вещей
Интернет вещей Предыстория информатики 9 класс
Предыстория информатики 9 класс Организация вычислений в Excel. Тест
Организация вычислений в Excel. Тест Компьютерная графика
Компьютерная графика Онлайн магазин Avon
Онлайн магазин Avon Печатать ПРЕЗЕНТАЦИЯ
Печатать ПРЕЗЕНТАЦИЯ Программа LabVIEW
Программа LabVIEW Предметно-ориентированное проектирование автоматизированных систем управления. Раздел 2. Технологии DDD
Предметно-ориентированное проектирование автоматизированных систем управления. Раздел 2. Технологии DDD Структура как пользовательский тип и совокупность данных
Структура как пользовательский тип и совокупность данных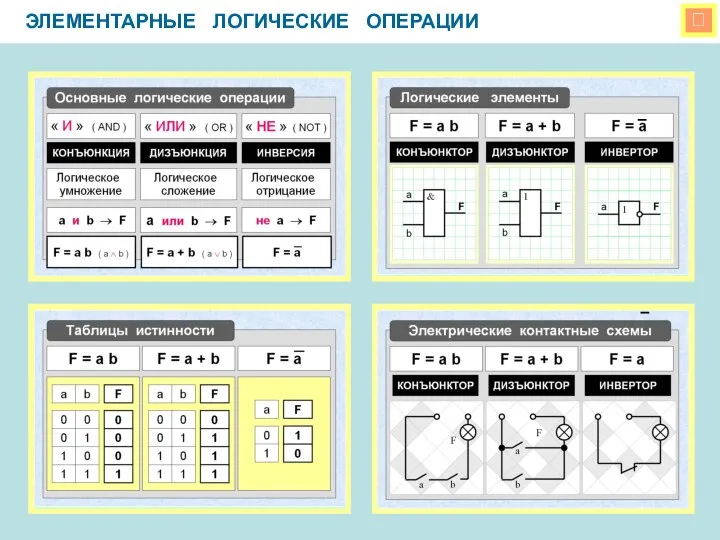 Элементарные логические операции
Элементарные логические операции Системный блок
Системный блок Инновации в видеоиграх
Инновации в видеоиграх Кодирование звуковой информации. Представление информации в компьютере
Кодирование звуковой информации. Представление информации в компьютере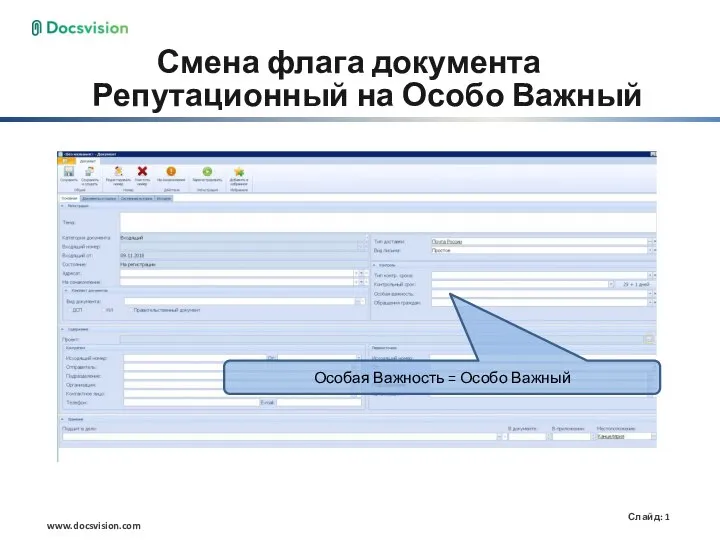 Смена флага документа репутационный на особо важный
Смена флага документа репутационный на особо важный Скорочтение
Скорочтение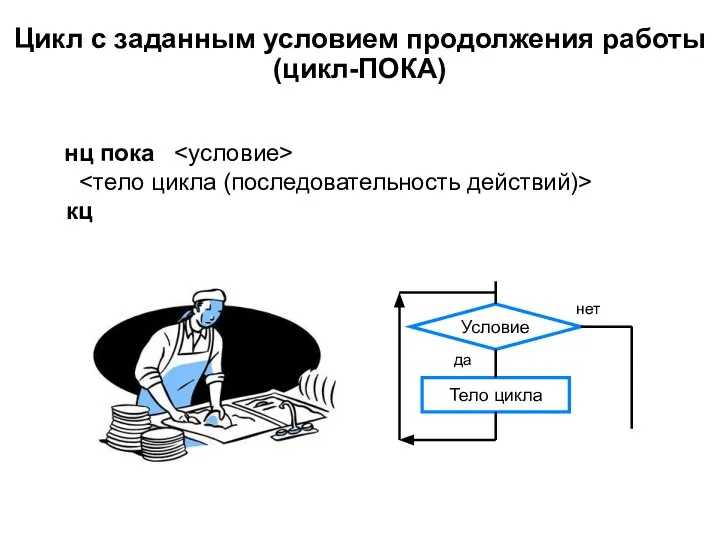 Цикл с заданным условием продолжения работы (цикл-Пока)
Цикл с заданным условием продолжения работы (цикл-Пока) Технологический цикл обработки информации на компьютере. Лекция 2
Технологический цикл обработки информации на компьютере. Лекция 2