Содержание
- 2. 2 При нулевой гипотезе предполагается, что коэффициент является определенным значением. А согласно альтернативной гипотезе, коэффициентом может
- 3. 3 Однако иногда мы можем сказать,что если нулевая гипотеза не верна, то коэффициент не может быть
- 4. 4 В других случаях мы могли бы утверждать, что, если нулевая гипотеза не верна, то коэффициент
- 5. 5 Теория, лежащая в основе односторонних тестов, в частности, выигрыш в компромиссе между размером (уровнем значимости)
- 6. 6 Эта последовательность предполагает хорошее понимание этого материала. Нулевая гипотеза Альтернативная гипотеза T статистика Отвергается H0
- 7. 7 Возвращаясь к модели инфляции цен / заработной платы, мы увидели, что не можем отвергнуть нулевую
- 8. 8 Однако на практике повышение производительности может привести к тому, что темпы инфляции издержек и, следовательно,
- 9. 9 Конечно, повышение производительности труда не приведет к тому, что инфляция цен превысит инфляцию заработной платы,
- 10. 10 Таким образом, мы можем выполнить односторонний тест, для которого критическое значение t с 18 степенями
- 11. 11 Теперь рассмотрим особый, но очень распространенный случай H0: b2 = 0. Модель Y = β1
- 12. 12 Это происходит, когда вы хотите продемонстрировать, что переменная X влияет на другую переменную Y. Устанавливается
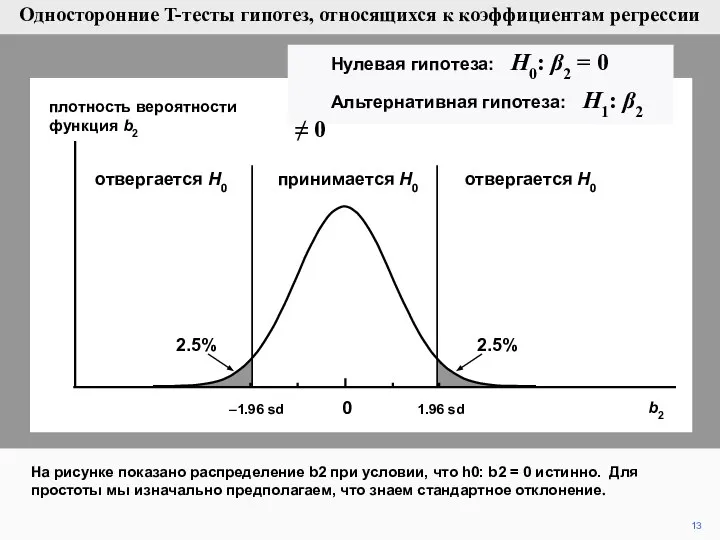
- 13. 13 плотность вероятности функция b2 На рисунке показано распределение b2 при условии, что h0: b2 =
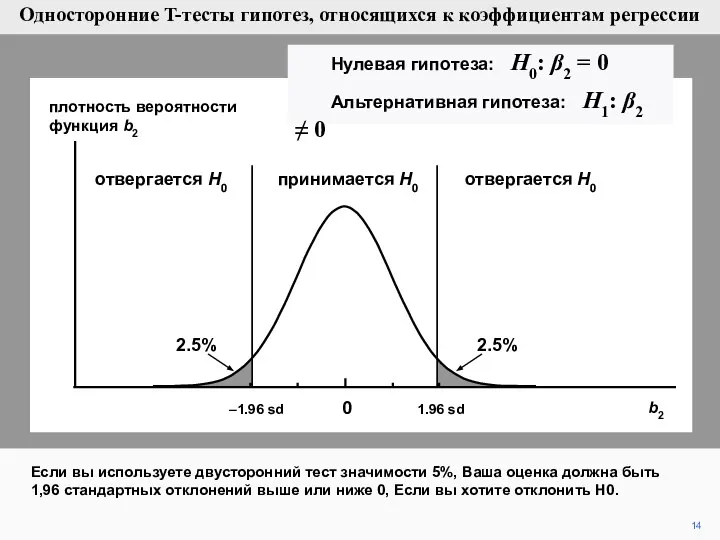
- 14. 14 плотность вероятности функция b2 Если вы используете двусторонний тест значимости 5%, Ваша оценка должна быть
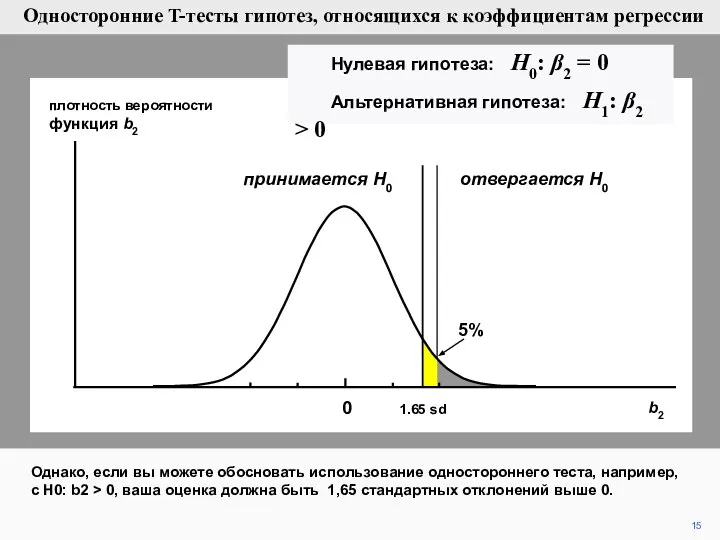
- 15. 15 плотность вероятности функция b2 Однако, если вы можете обосновать использование одностороннего теста, например, с H0:
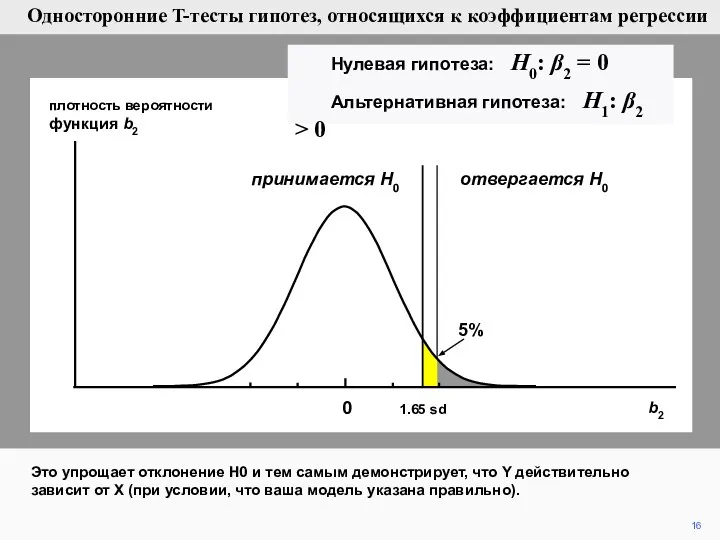
- 16. 16 плотность вероятности функция b2 0 отвергается H0 принимается H0 1.65 sd Это упрощает отклонение H0
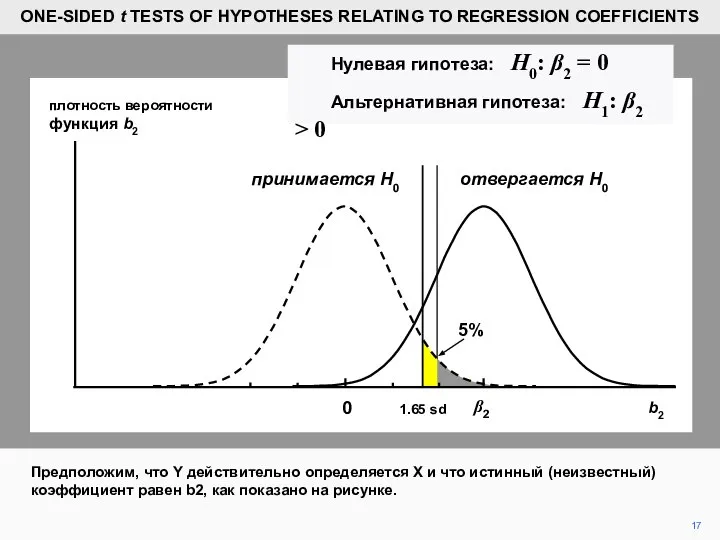
- 17. 17 плотность вероятности функция b2 Предположим, что Y действительно определяется X и что истинный (неизвестный) коэффициент
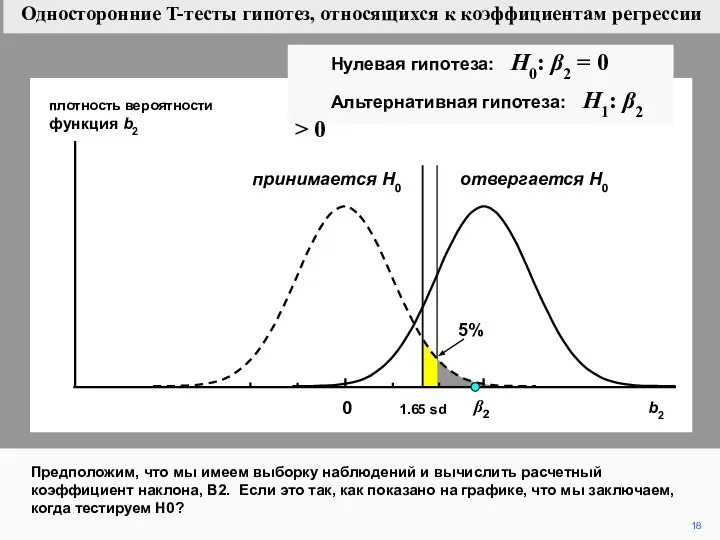
- 18. 18 плотность вероятности функция b2 Предположим, что мы имеем выборку наблюдений и вычислить расчетный коэффициент наклона,
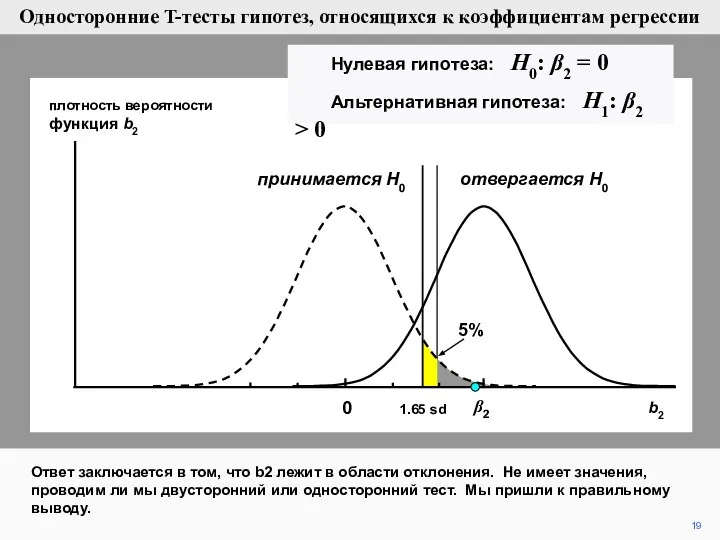
- 19. 19 плотность вероятности функция b2 Ответ заключается в том, что b2 лежит в области отклонения. Не
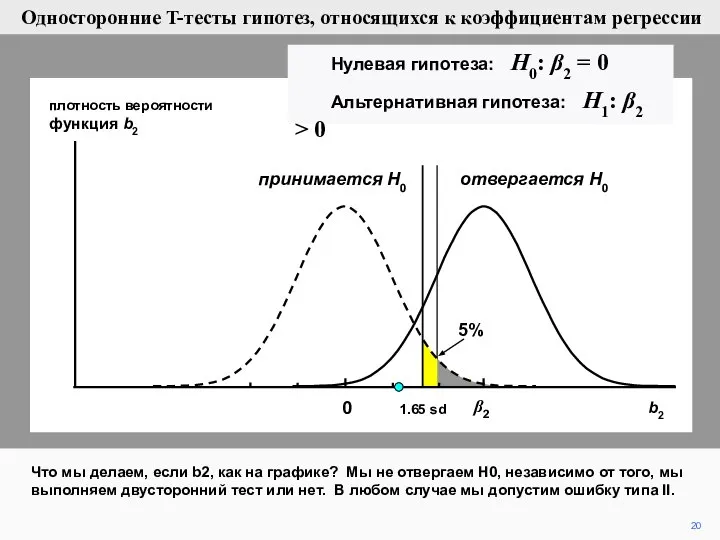
- 20. 20 плотность вероятности функция b2 Что мы делаем, если b2, как на графике? Мы не отвергаем
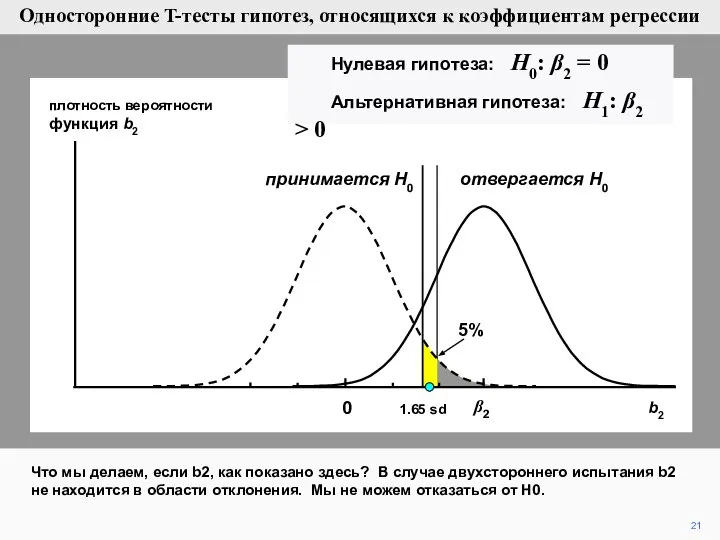
- 21. 21 плотность вероятности функция b2 Что мы делаем, если b2, как показано здесь? В случае двухстороннего
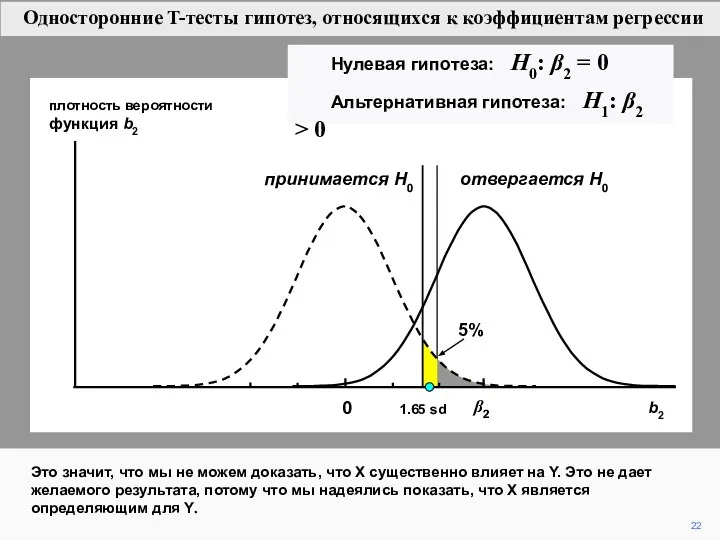
- 22. 22 плотность вероятности функция b2 Это значит, что мы не можем доказать, что X существенно влияет
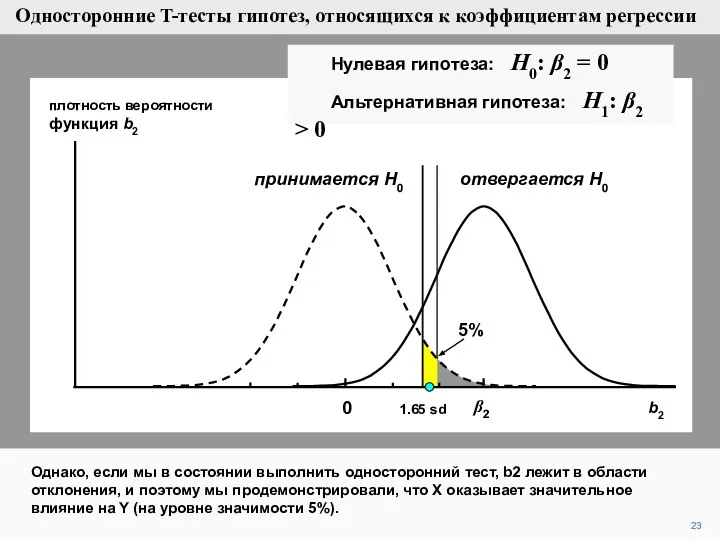
- 23. 23 плотность вероятности функция b2 Однако, если мы в состоянии выполнить односторонний тест, b2 лежит в
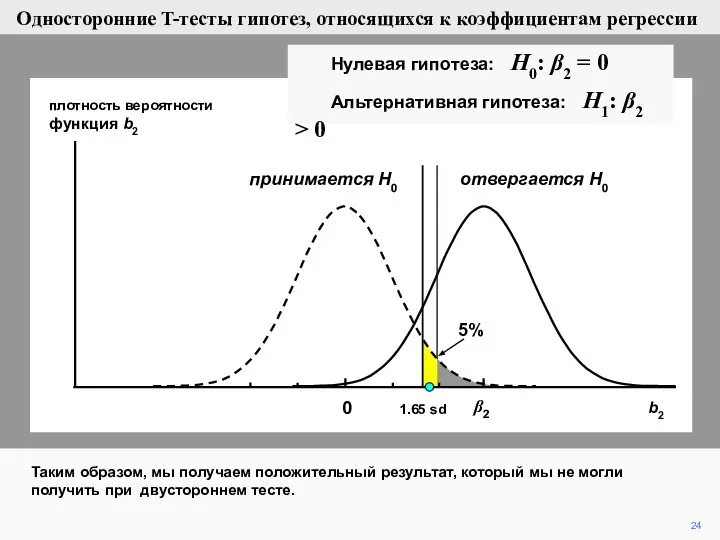
- 24. 24 плотность вероятности функция b2 0 отвергается H0 принимается H0 1.65 sd β2 Таким образом, мы
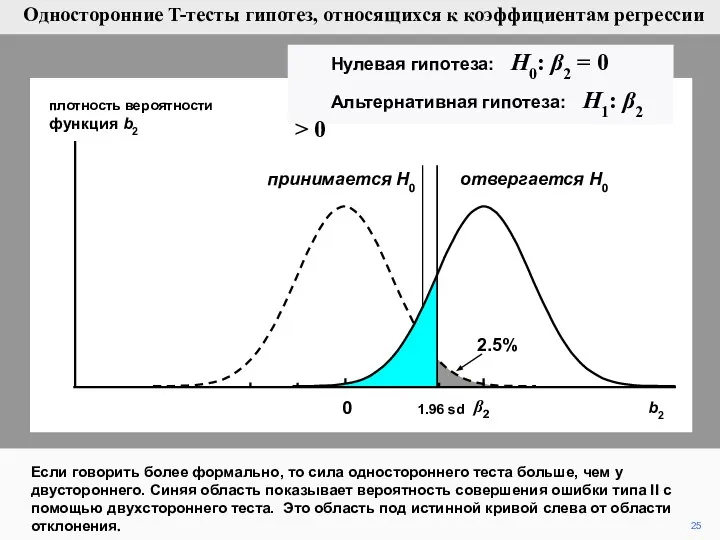
- 25. 25 плотность вероятности функция b2 0 отвергается H0 принимается H0 β2 Если говорить более формально, то
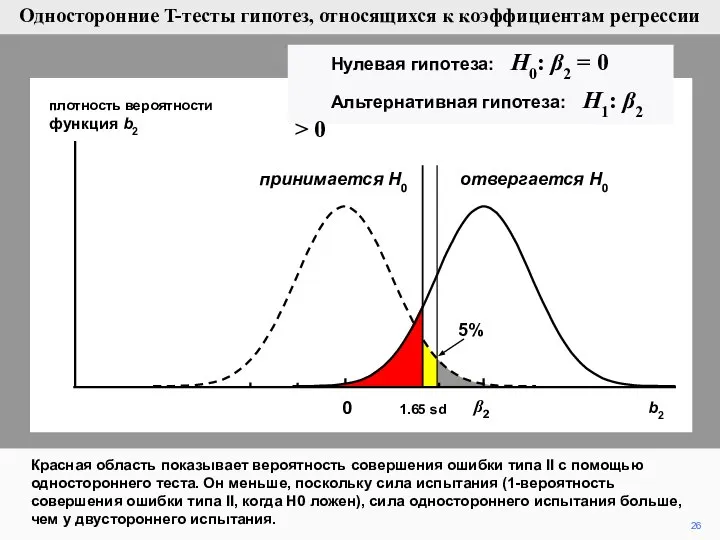
- 26. 26 плотность вероятности функция b2 0 отвергается H0 принимается H0 1.65 sd β2 Красная область показывает
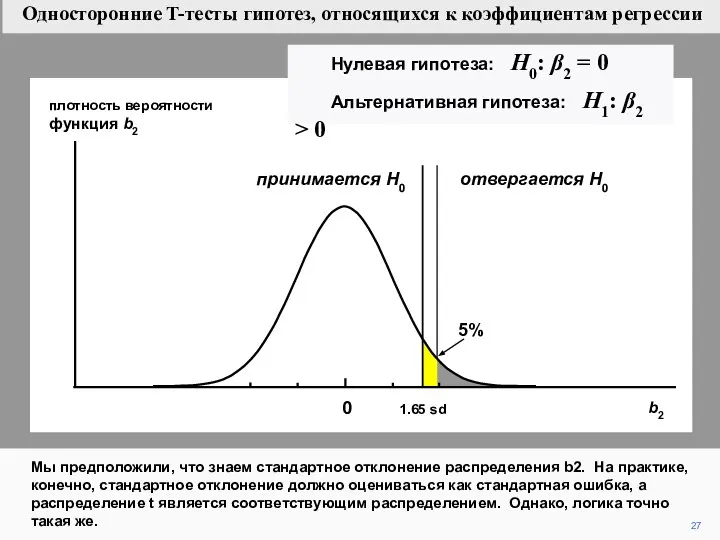
- 27. Мы предположили, что знаем стандартное отклонение распределения b2. На практике, конечно, стандартное отклонение должно оцениваться как
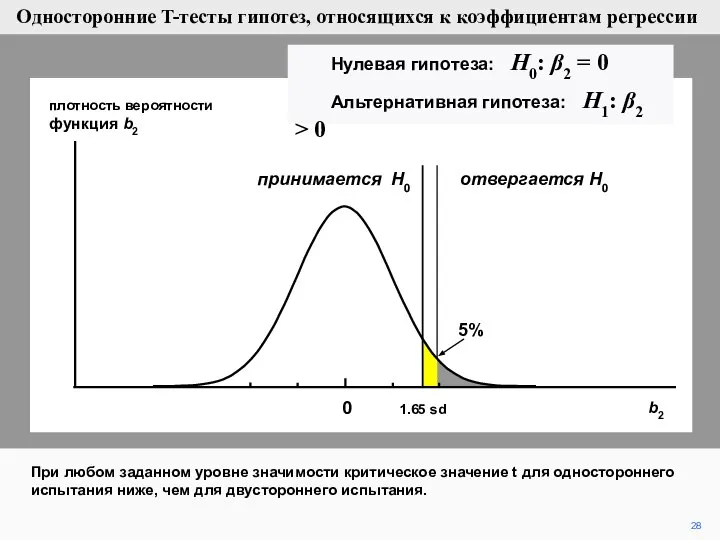
- 28. При любом заданном уровне значимости критическое значение t для одностороннего испытания ниже, чем для двустороннего испытания.
- 30. Скачать презентацию











 Программное обеспечение компьютера
Программное обеспечение компьютера GIT. Семантические конфликты
GIT. Семантические конфликты BlockChain
BlockChain Функциональное программирование
Функциональное программирование Основные алгоритмические конструкции
Основные алгоритмические конструкции Моделі системи глобальної інформаційної безпеки. Існуючі моделі
Моделі системи глобальної інформаційної безпеки. Існуючі моделі Программы-детекторы
Программы-детекторы Работа с функциями в табличном процессоре Excel
Работа с функциями в табличном процессоре Excel Задачи информатизации общества
Задачи информатизации общества Как играть в cuphead
Как играть в cuphead Программное обеспечение компютера(Гармашев Илья 7Б)
Программное обеспечение компютера(Гармашев Илья 7Б)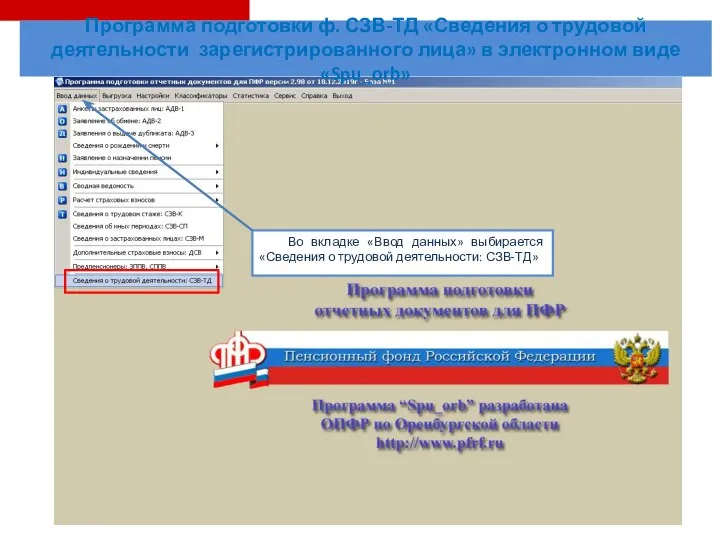 Программа подготовки СЗВ-ТД Сведения о трудовой деятельности зарегистрированного лица в электронном виде Spu_orb
Программа подготовки СЗВ-ТД Сведения о трудовой деятельности зарегистрированного лица в электронном виде Spu_orb Турист v1.0. Программа автоматизации составления документов и отчетов
Турист v1.0. Программа автоматизации составления документов и отчетов Листовое моделирование. Создание детали Совок металлический
Листовое моделирование. Создание детали Совок металлический Техника безопасности. Правила работы на компьютере
Техника безопасности. Правила работы на компьютере Разговор с компьютером
Разговор с компьютером Двоичная куча – пирамида (binary heap)
Двоичная куча – пирамида (binary heap) Основные понятия программной инженерии. Принципы проектирования сложных программных систем. Лекции 1
Основные понятия программной инженерии. Принципы проектирования сложных программных систем. Лекции 1 Искусственный интеллект в образовании
Искусственный интеллект в образовании Компьютерные презентации
Компьютерные презентации Блочный шифр Crab
Блочный шифр Crab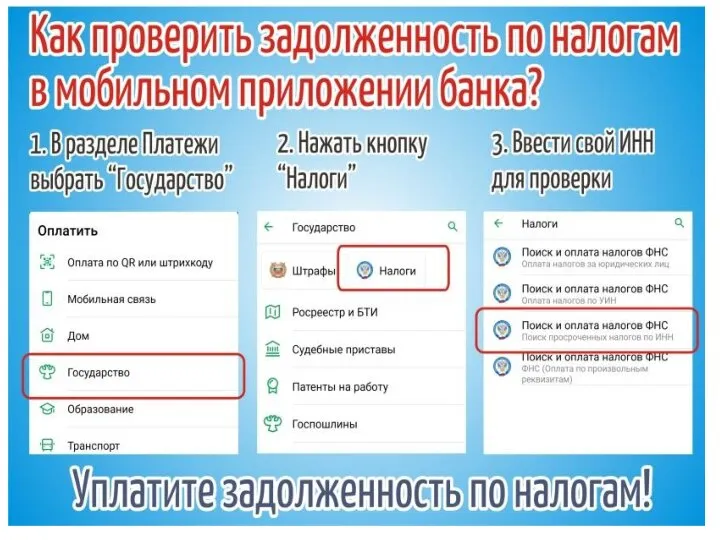 Листовка по оплате задолженности СбербанкОнлайн
Листовка по оплате задолженности СбербанкОнлайн Tabular information
Tabular information Некоторые сведения из теории множеств. Элементы теории множеств и алгебры логики
Некоторые сведения из теории множеств. Элементы теории множеств и алгебры логики Avatar music
Avatar music Тест Аэробика
Тест Аэробика Вычислите объем в байтах
Вычислите объем в байтах Продажа металлолома и сырых шкур
Продажа металлолома и сырых шкур