Operations on Bits

After reading this chapter, the reader should be able to:
OBJECTIVES

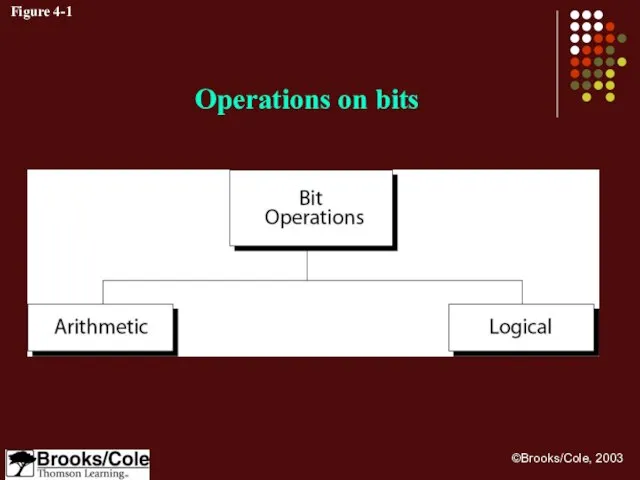
Figure 4-1
Operations on bits

ARITHMETIC
OPERATIONS
4.1

Arithmetic operations
Arithmetic operations involve:
Adding (+)
Subtracting (--)
Multiplying (X)
Dividing (/)
And so on…

Table 4.1 Adding bits
Number of 1s
------------
None
One
Two
Three
Result
------------
0
1
0
1
Carry
------------
-
-
1
1
Addition in two’s complement

Rule of Adding Integers in
Two’s Complement
Add 2 bits and propagate the carry to the next column. If there is a final carry after the leftmost column addition, discard (捨棄) it.

Example 1
Add two numbers in two’s complement representation: (+17) + (+22) ? (+39)
Solution
Carry 1
0 0 0 1 0 0 0 1 +
0 0 0 1 0 1 1 0
----------------------------------
Result 0 0 1 0 0 1 1 1 ? 39

Example 2
Add two numbers in two’s complement representation: (+24) + (-17) ? (+7)
Solution
Carry 1 1 1 1 1
0 0 0 1 1 0 0 0 +
1 1 1 0 1 1 1 1
----------------------------------
Result 0 0 0 0 0 1 1 1 ? +7

Example 3
Add two numbers in two’s complement representation: (-35) + (+20) ? (-15)
Solution
Carry 1 1 1
1 1 0 1 1 1 0 1 +
0 0 0 1 0 1 0 0
----------------------------------
Result 1 1 1 1 0 0 0 1 ? -15

Example 4
Add two numbers in two’s complement representation: (+127) + (+3) ? (+130)
Solution
Carry 1 1 1 1 1 1 1
0 1 1 1 1 1 1 1 +
0 0 0 0 0 0 1 1
----------------------------------
Result 1 0 0 0 0 0 1 0 ? -126 (Error)
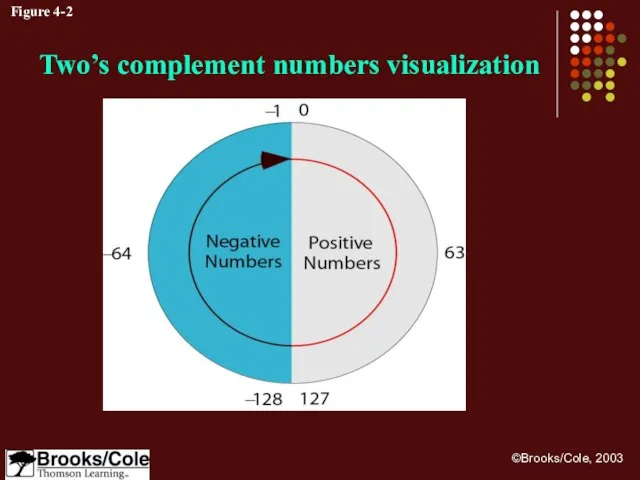
An overflow has occurred.

Range of numbers in two’s complement representation
- (2N-1) ---------- 0 ----------- +(2N-1 –1)
Note:

Figure 4-2
Two’s complement numbers visualization

When you do arithmetic operations on
numbers in a computer, remember that
each number and the result should be
in the range defined by the bit allocation.
Note:

Example 5
Subtract 62 from 101 in two’s complement: (+101) - (+62) ?? (+101) + (-62)
Solution
Carry 1 1
0 1 1 0 0 1 0 1 +
1 1 0 0 0 0 1 0
----------------------------------
Result 0 0 1 0 0 1 1 1 ? 39
The leftmost carry is discarded.
Subtraction in two’s complement

Arithmetic operations on floating-point numbers
Addition and subtraction for floating-point numbers are one process. (p. 54)
Check the sign. (a, b)
Move the decimal points to make the exponents the same.
Add or subtract the mantissas (底數).
Normalize the result before storing in memory.
Check for any overflow.

Example 6
Add two floats:
0 10000100 10110000000000000000000
0 10000010 01100000000000000000000
Solution
The exponents are 5 and 3. The numbers are:
+25 x 1.1011 and +23 x 1.011
Make the exponents the same.
(+25 x 1.1011)+ (+25 x 0.01011) ? +25 x 10.00001
After normalization +26 x 1.000001, which is stored as:
0 10000101 000001000000000000000000
Addition

LOGICAL
OPERATIONS
4.2

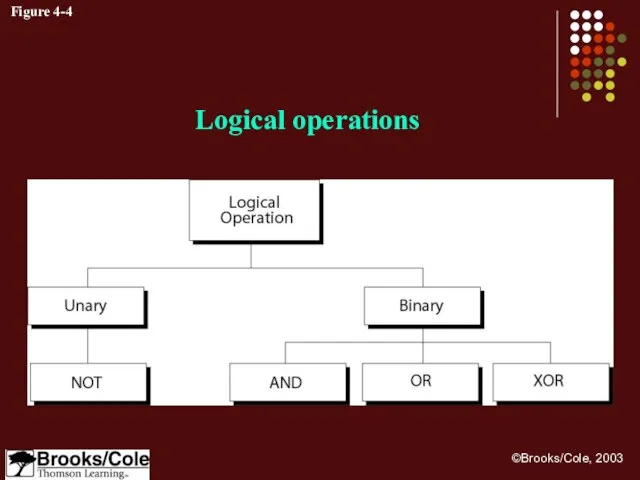
Logical operations
A logical operation can accept 1 or 2 bits to create only 1 bit.
Unary operation (Figure4.3)
Binary operation (Figure4.3)

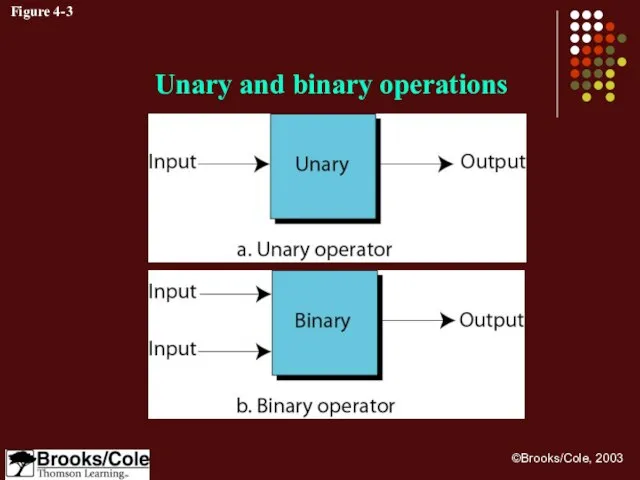
Figure 4-3
Unary and binary operations

Figure 4-4
Logical operations

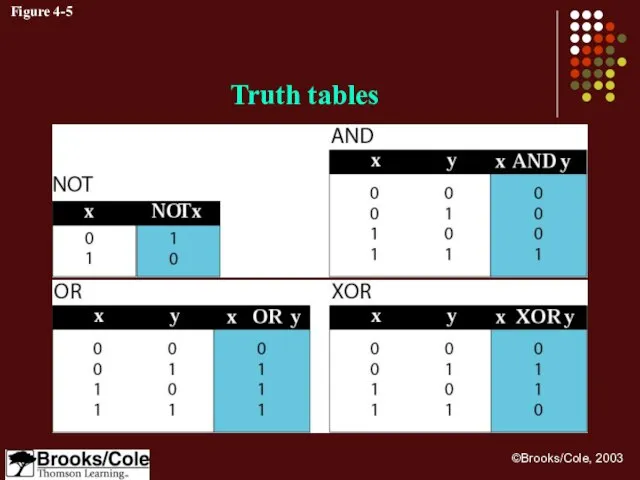
Figure 4-5
Truth tables

Figure 4-6
Unary operator -- NOT operator

Example 7
Use the NOT operator on the bit pattern 10011000
Solution
Target 1 0 0 1 1 0 0 0 NOT
------------------
Result 0 1 1 0 0 1 1 1
NOT operator

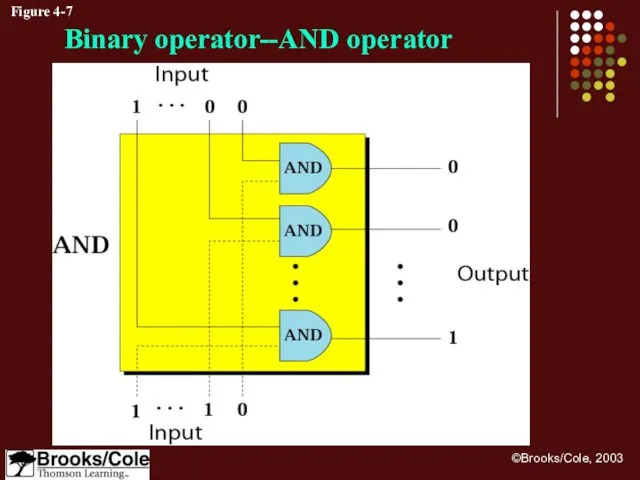
Figure 4-7
Binary operator--AND operator

Example 8
Use the AND operator on bit patterns 10011000 and 00110101.
Solution
Target 1 0 0 1 1 0 0 0 AND
0 0 1 1 0 1 0 1
------------------
Result 0 0 0 1 0 0 0 0
AND operator

Figure 4-8
Inherent (本質的) rule of the AND operator

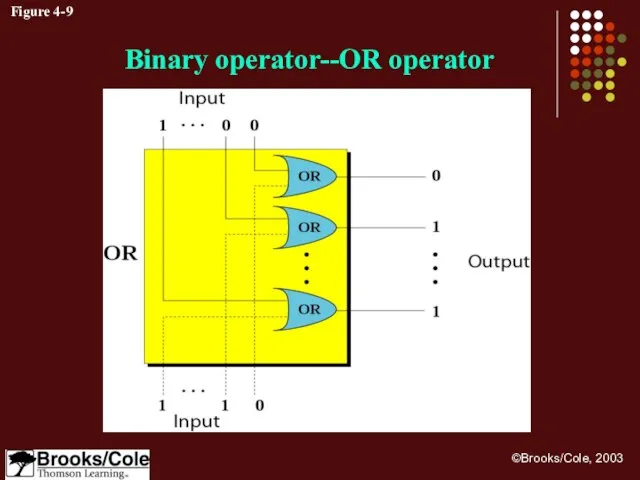
Figure 4-9
Binary operator--OR operator

Example 9
Use the OR operator on bit patterns 10011000 and 00110101
Solution
Target 1 0 0 1 1 0 0 0 OR
0 0 1 1 0 1 0 1
------------------
Result 1 0 1 1 1 1 0 1
OR operator

Figure 4-10
Inherent rule of the OR operator

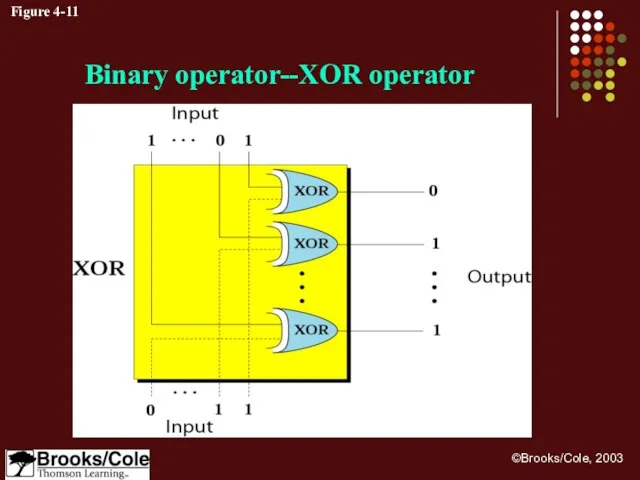
Figure 4-11
Binary operator--XOR operator

Example 10
Use the XOR operator on bit patterns 10011000 and 00110101.
Solution
Target 1 0 0 1 1 0 0 0 XOR
0 0 1 1 0 1 0 1
------------------
Result 1 0 1 0 1 1 0 1
XOR operator

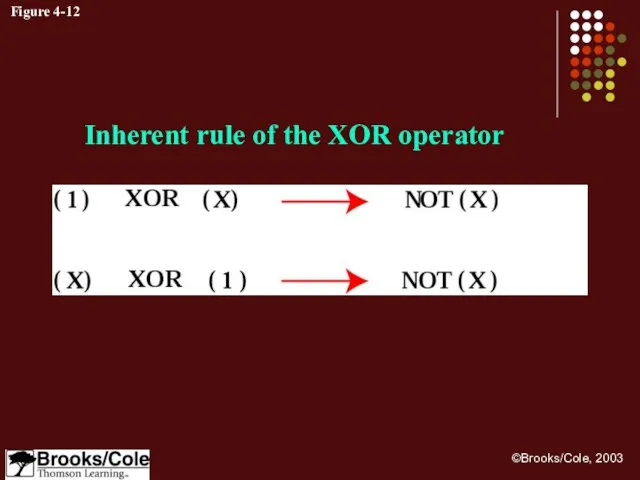
Figure 4-12
Inherent rule of the XOR operator

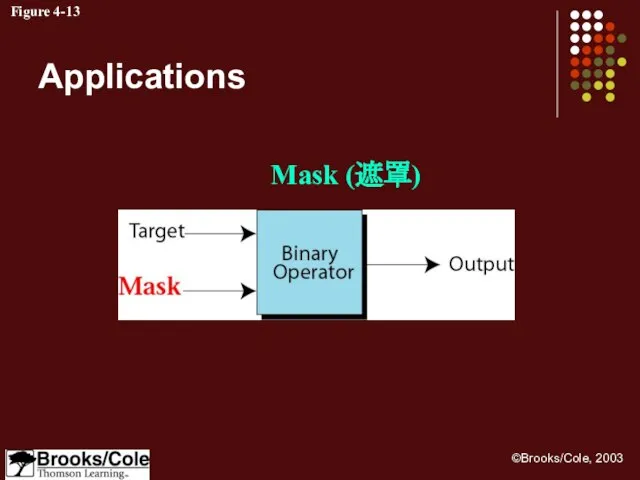
Figure 4-13
Mask (遮罩)
Applications

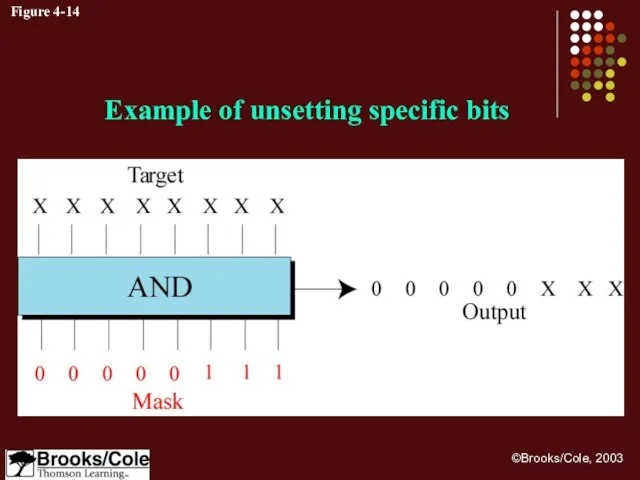
Figure 4-14
Example of unsetting specific bits

Example 11
Use a mask to unset (clear) the 5 leftmost bits of a pattern. Test the mask with the pattern 10100110.
Solution
The mask is 00000111.
Target 1 0 1 0 0 1 1 0 AND
Mask 0 0 0 0 0 1 1 1
------------------
Result 0 0 0 0 0 1 1 0

Example 12
Imagine a power plant (水力發電廠) that pumps water (供水) to a city using eight pumps (抽水機). The state of the pumps (on or off) can be represented by an 8-bit pattern. For example, the pattern 11000111 shows that pumps 1 to 3 (from the right), 7 and 8 are on while pumps 4, 5, and 6 are off. Now assume pump 7 shuts down. How can a mask show this situation?
Solution on the next slide.

Use the mask 10111111 to AND with the target pattern. The only 0 bit (bit 7) in the mask turns off the seventh bit in the target.
Target 1 1 0 0 0 1 1 1 AND
Mask 1 0 1 1 1 1 1 1
------------------
Result 1 0 0 0 0 1 1 1
Solution

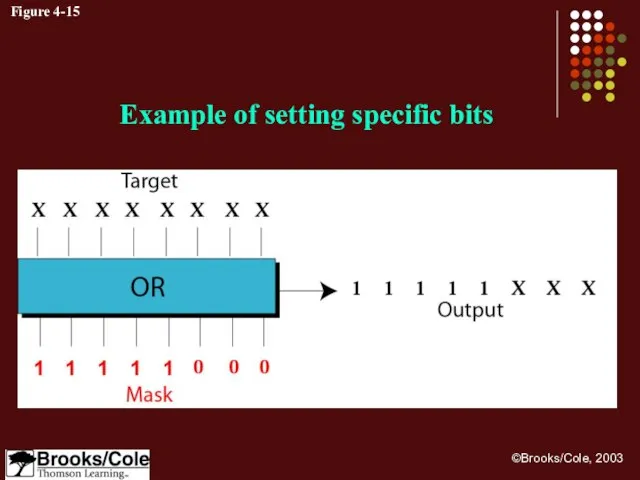
Figure 4-15
Example of setting specific bits

Example 13
Use a mask to set the 5 leftmost bits of a pattern. Test the mask with the pattern 10100110.
Solution
The mask is 11111000.
Target 1 0 1 0 0 1 1 0 OR
Mask 1 1 1 1 1 0 0 0
------------------
Result 1 1 1 1 1 1 1 0

Example 14
Using the power plant example, how can you use a mask to to show that pump 6 is now turned on?
Solution
Use the mask 00100000.
Target 1 0 0 0 0 1 1 1 OR
Mask 0 0 1 0 0 0 0 0
------------------
Result 1 0 1 0 0 1 1 1

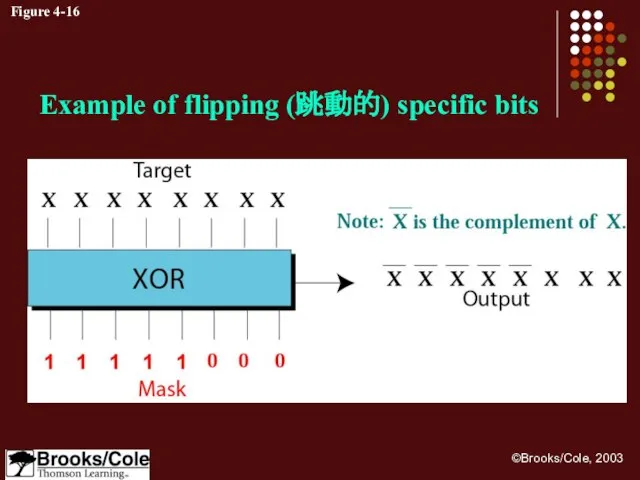
Figure 4-16
Example of flipping (跳動的) specific bits

Example 15
Use a mask to flip the 5 leftmost bits of a pattern. Test the mask with the pattern 10100110.
Solution
Target 1 0 1 0 0 1 1 0 XOR
Mask 1 1 1 1 1 0 0 0
------------------
Result 0 1 0 1 1 1 1 0

SHIFT
OPERATIONS
4.3

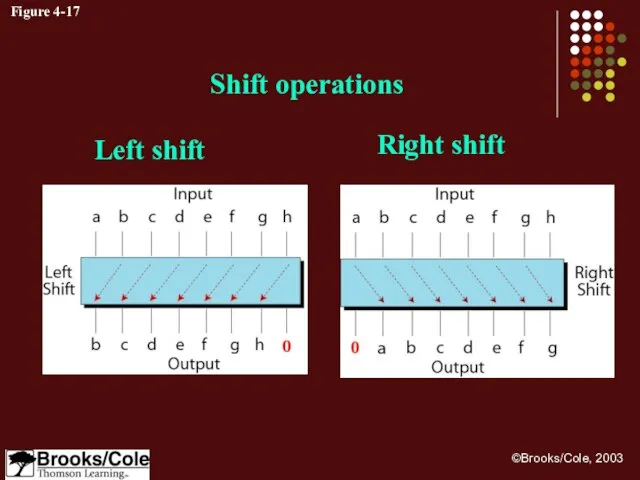
Figure 4-17
Shift operations
Right shift
Left shift

Solution
If a bit pattern represents an unsigned number, a right-shift operation divides the number by two. The pattern 00111011 represents 59. When you shift the number to the right, you get 00011101, which is 29. If you shift the original number to the left, you get 01110110, which is 118.
Example 16
Show how you can divide or multiply a number by
2 using shift operations.

Example 17
Use the mask 00001000 to AND with the target to keep the fourth bit and clear the rest of the bits.
Solution
Use a combination of logical and shift operations to find the value (0 or 1) of the fourth bit (from the right).
Continued on the next slide

Solution (continued)
Target a b c d e f g h AND
Mask 0 0 0 0 1 0 0 0
------------------
Result 0 0 0 0 e 0 0 0
Shift the new pattern three times to the right
0000e000 ? 00000e00 ? 000000e0 ? 0000000e
Now it is easy to test the value of the new pattern as an unsigned integer. If the value is 1, the original bit was 1; otherwise the original bit was 0.