Операции над графами. Практическая работа 01

для студентов специальности 09.02.02 «Компьютерные сети»
Тема: Операции над графами
Цель работы: Приобрести навыки выполнения операций над графами, построения матриц смежности.
Норма времени: 2 часа.
После выполненных работ студент должен знать: определение основных операций над графами.
уметь: строить матрицы смежности для результатов операций над графами.
Практическая работа № 1

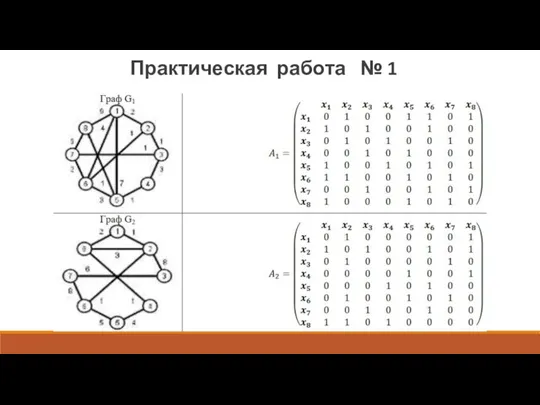
Бинарные операции.
Объединение графов ?1 и ?2, обозначаемое как ?1∪?2, представляет такой граф ?3=(?1∪?2, ?1∪?2), что множество его вершин является объединением Х1 и Х2, а множество ребер –объединением A1 и A2.
Матрица смежности результирующего графа получается операцией поэлементного логического сложения матриц смежности исходных графов G1и G2.
Практическая работа № 1

Практическая работа № 1

Практическая работа № 1

Пересечение графов G1и G2, обозначаемое как ?1∩?2, представляет собой граф ?4=(?1∩?2, ?1∩?2).
Таким образом, множество вершин графа G4 состоит из вершин, присутствующих одновременно в G1 и G2.
Результирующая матрица смежности получается операцией поэлементного логического умножения матриц смежности исходных графов.
Практическая работа № 1

Кольцевая сумма двух графов G1 и G2, обозначаемая как ?1⨁?2, представляет собой граф G5, порожденный на множестве ребер ?1⨁?2.
Другими словами, граф G5 не имеет изолированных вершин и состоит только из ребер, присутствующих либо в G1, либо в G2, но не в обоих одновременно.
Результирующая матрица смежности получается операцией поэлементного логического сложения матриц смежности исходных графов
Практическая работа № 1

Унарные операции.
Удаление вершины.
При удалении вершины удаляются и все ребра, инцидентные этой вершине.
Результирующая матрица смежности графа после удаления вершины хi получается путем удаления соответствующего i-го столбца и i-ой строки из исходной матрицы.
Практическая работа № 1

Удаление ребра или удаление дуги.
Концевые вершины дуги ai не удаляются.
Результирующая матрица смежности графа после выполнения операции удаления дуги ai получается путем удаления соответствующих элементов из исходной матрицы.
Практическая работа № 1

Замыкание или отождествление.
Говорят, что пара вершин хi и xj в графе G замыкается (или отождествляется), если они заменяются такой новой вершиной, что все дуги в графе G, инцидентные хi и xj, становятся инцидентными новой вершине.
Матрица смежности графа после выполнения операции замыкания вершин хi и xj получается путем поэлементного логического сложения i-го и j-го столбцов и i-ой и j-строк в исходной матрице и "сжимания" матрицы по вертикали и горизонтали.
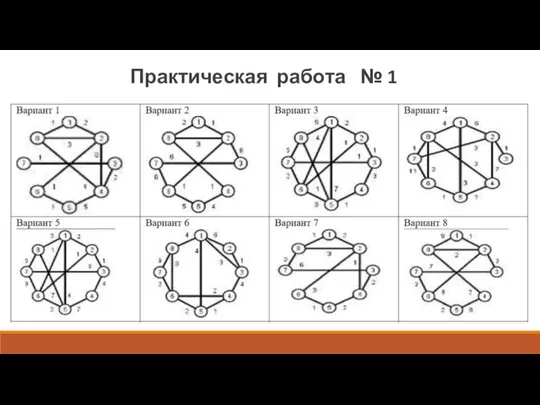
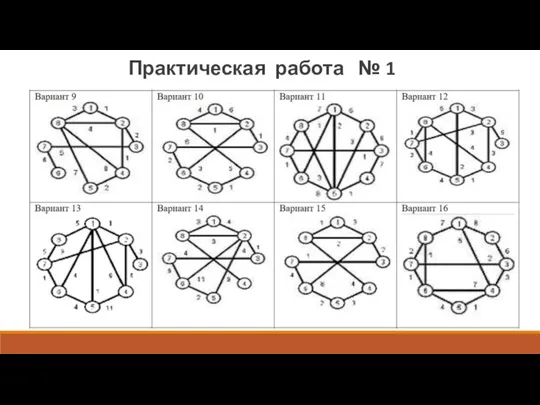
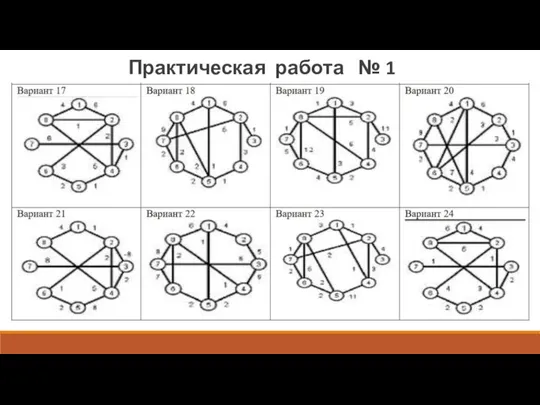
Практическая работа № 1

Задания для самостоятельного выполнения:
Задание 1.
Бинарные операции.
Записать результаты операций объединения, пересечения, кольцевой суммы графов.
Задание 2.
Унарные операции.
Записать результат удаления вершины 1, ребра 4-5, замыкания вершин 6-7.
Практическая работа № 1

ПРИМЕР ОТЧЕТА О ПРАКТИЧЕСКОМ ЗАНЯТИИ
Исходные графы и их матрицы смежности: варианты ..., ...
Практическая работа № 1

Практическая работа № 1

Практическая работа № 1

Практическая работа № 1

Практическая работа № 1