Содержание
- 2. Историческая справка (1815 -1864) Английский математик Джордж Буль разработал основы алгебры, в которой используются только 0
- 3. Алгебра логики – это математический аппарат, с помощью которого записывают (кодируют), упрощают, вычисляют и преобразовывают логические
- 4. Формы мышления 1. Понятие. 2. Высказывание. 3. Умозаключение. Понятие – форма мышления, фиксирующая основные, существенные признаки
- 5. Высказывание – повествовательное предложение, о котором можно сказать, истинно оно или ложно. Умозаключение – это форма
- 6. Высказывание Высказывание может быть либо истинно, либо ложно. Высказывания могут быть выражены с помощью естественных и
- 7. Логические операции Логическое умножение Объединение двух (или нескольких) высказываний в одно с помощью союза «и» («а»,
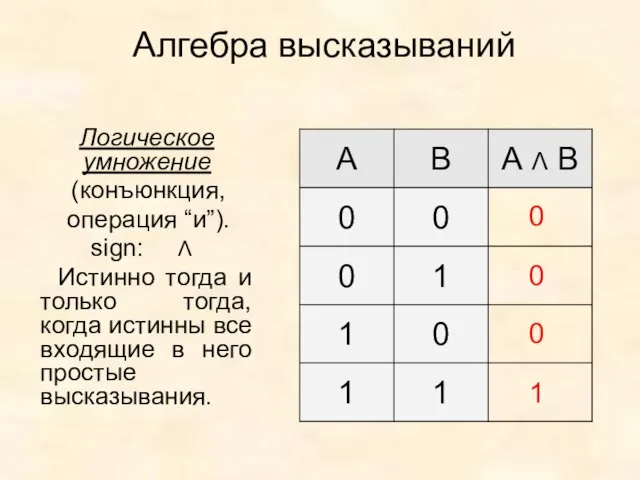
- 8. Алгебра высказываний Логическое умножение (конъюнкция, операция “и”). sign: Λ Истинно тогда и только тогда, когда истинны
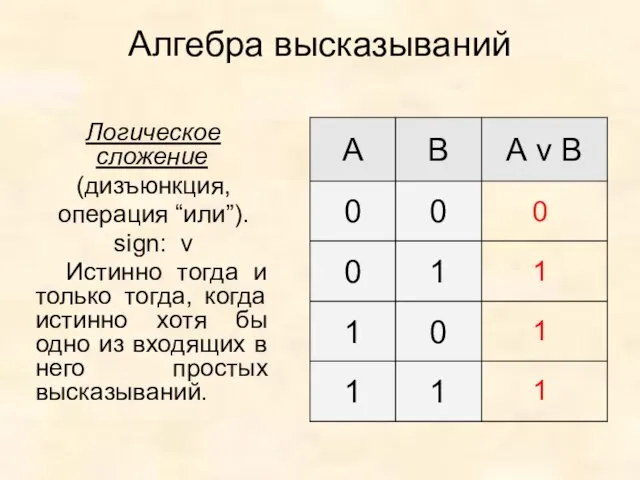
- 9. Алгебра высказываний Логическое сложение (дизъюнкция, операция “или”). sign: v Истинно тогда и только тогда, когда истинно
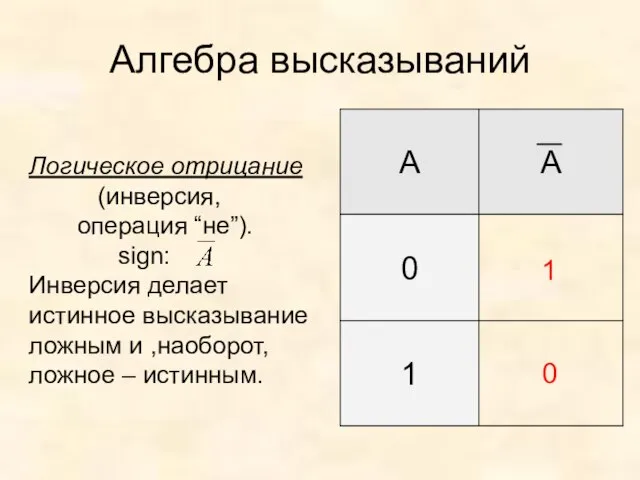
- 10. Алгебра высказываний Логическое отрицание (инверсия, операция “не”). sign: Инверсия делает истинное высказывание ложным и ,наоборот, ложное
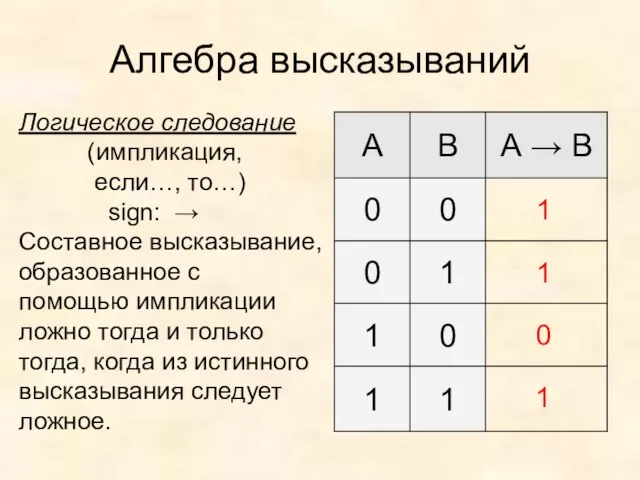
- 11. Алгебра высказываний Логическое следование (импликация, если…, то…) sign: → Составное высказывание, образованное с помощью импликации ложно
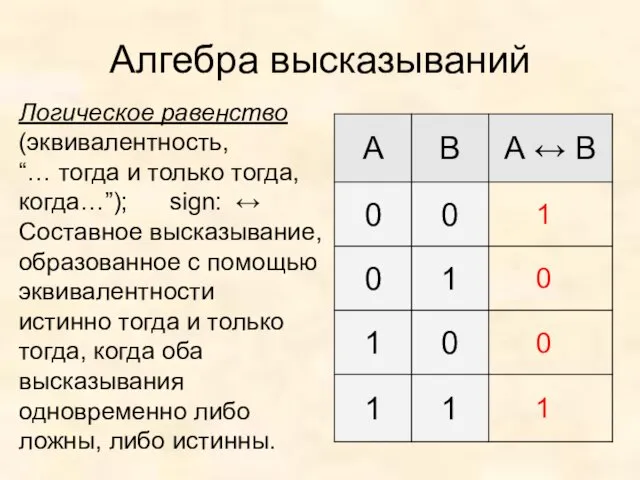
- 12. Алгебра высказываний Логическое равенство (эквивалентность, “… тогда и только тогда, когда…”); sign: ↔ Составное высказывание, образованное
- 14. Скачать презентацию






 Web-программирование. Лекция 5. Шаблоны проектирования
Web-программирование. Лекция 5. Шаблоны проектирования Правила работы и безопасного поведения в компьютерном классе
Правила работы и безопасного поведения в компьютерном классе Использование облачных технологий в деятельности педагога
Использование облачных технологий в деятельности педагога Известия VS Медиазона
Известия VS Медиазона Аудит divine-light.ru_версия 21092022
Аудит divine-light.ru_версия 21092022 Основы музейных коммуникаций
Основы музейных коммуникаций Internet Protocol (IP)
Internet Protocol (IP) ВКонтакте - российская социальная сеть
ВКонтакте - российская социальная сеть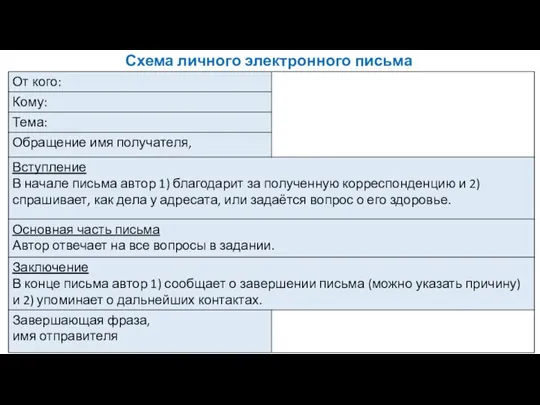 Схема личного электронного письма
Схема личного электронного письма Мобильное электронное образование в детских садах и дома
Мобильное электронное образование в детских садах и дома Базовые показатели эффективности (БПЭ)
Базовые показатели эффективности (БПЭ) Представление звуковой информации
Представление звуковой информации Технология промышленного производства
Технология промышленного производства Сеть для организаций. Отчет о проектной работе
Сеть для организаций. Отчет о проектной работе Умные таблицы Excel 2007-2013
Умные таблицы Excel 2007-2013 Строки как одномерные массивы данных типа char (терминальные строки)
Строки как одномерные массивы данных типа char (терминальные строки) Азбука журналистики
Азбука журналистики Краудсорсинг в ИТ рекрутменте
Краудсорсинг в ИТ рекрутменте Метрология и теория измерений
Метрология и теория измерений одирование тестовой, графической и звуковой информации
одирование тестовой, графической и звуковой информации Вводное занятие. Система отслеживания багов и задач JIRA (лекция - 3)
Вводное занятие. Система отслеживания багов и задач JIRA (лекция - 3) Инструкция по входу в ZOOM
Инструкция по входу в ZOOM Das At-Zeichen
Das At-Zeichen Презентация на тему Поколение ЭВМ
Презентация на тему Поколение ЭВМ  Понятие информация
Понятие информация Web - страницы. Язык HTML
Web - страницы. Язык HTML Ресурсы для защиты информации в веке IT технологий
Ресурсы для защиты информации в веке IT технологий Одномерные массивы целых чисел. Описание, заполнение, вывод массива
Одномерные массивы целых чисел. Описание, заполнение, вывод массива