Основы оценки сложности алгоритмов. Поиск НОД и НОК. Системы счисления

Занятие 2.
Основы оценки сложности алгоритмов.
Поиск НОД и НОК.
Системы счисления

Знакомство с понятием
сложности алгоритма
При сравнении производительности различных алгоритмов решения задачи следует учитывать, что скорость выполнения компьютерных программ зависит от:
вычислительной производительности процессора ЭВМ,
объема кэш-памяти, оперативной памяти,
скорости доступа к запоминающим устройствам и т.п.
Поэтому время работы программы измеряется количеством операций
Главную роль играет характер возрастания числа элементарных операций при увеличении объема данных в задаче.
Кроме того, обычно учитывают объем памяти, которая используется во время работы программы
Эффективным решением олимпиадной задачи является такое, что:
укладывается в ограничения по времени работы программы
укладывается в ограничения ресурсов памяти, требующейся для выполнения программы
написано за кратчайшее время

Сложность алгоритма
Сложность алгоритма – функция FA(n), определенная как наибольшее количество элементарных действий при решении задачи с объемом входных данных n с помощью алгоритма А
Например:
на вход подается n чисел, следует вычислить их сумму
тогда сложность алгоритма определяется количеством операций сложения и линейно зависит от n

Важные определения

Важные определения

Характер возрастания
сложности

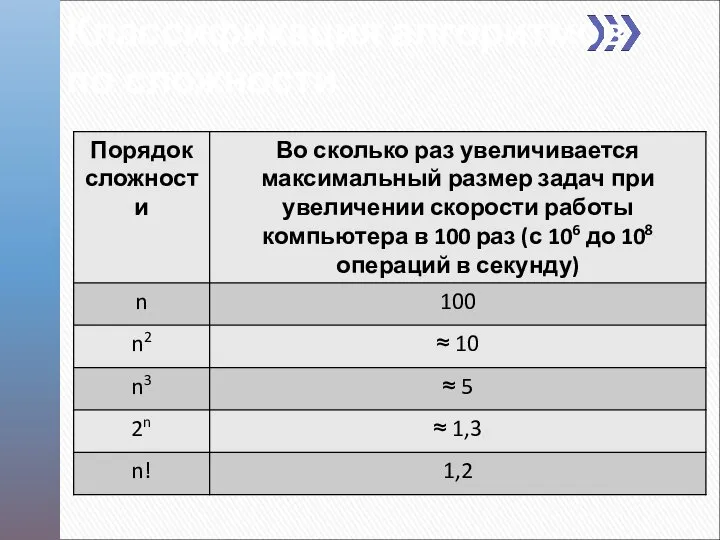
Классификация алгоритмов
по сложности

Примеры задач

Примеры задач

Бинарный алгоритм Евклида
Бинарный алгоритм Евклида выполняется примерно на 60% быстрее традиционного.
Бинарный алгоритм Евклида основан на соотношениях (a>b):

Поиск наименьшего общего кратного

b=a mod p -> остаток от деления a на p равен b
Пример: 5 mod 3=8 mod 3=2
Свойства арифметических операций
(a+b) mod p = ((a mod p) + (b mod p)) mod p
(a-b) mod p = (p + (a mod p) – (b mod p)) mod p, при а>b
-a mod p= (p-a) mod p
(a*b) mod p = ((a mod p) * (b mod p)) mod p
Аналогичной формулы для деления нет!
Поскольку обратный элемент по умножению существует только когда НОД (a, p)=1
Операцию деления можно выполнить только найдя обратный элемент по модулю p с помощью расширенного алгоритма
Арифметика остатков

Система счисления – система записи чисел с помощью определенного набора цифр
Цифры – символы, с помощью которых записываются числа в системе счисления
Алфавит – совокупность символов, используемых для записи чисел
Основание системы счисления – количество цифр, используемых для записи чисел
Позиционная система счисления – система счисления, в которой количественный эквивалент цифры зависит от ее положения в записи числа
5047 = 5*1000 + 0*100 + 4*10 + 7*1
Позиционные
системы счисления (ПСС)

Базис ПСС – последовательность чисел, каждое из которых задает «вес» соответствующего разряда
Традиционная ПСС – система счисления, базис которой образуют члены геометрической прогрессии,
знаменатель P>1 – натуральное число,
значения цифр – целые числа
…, P-3, P-2, P-1, 1, P1, P2, P3, …
P – основание P-ричной системы счисления
Примеры нетрадиционных СС
Фибоначчиева система счисления
Алфавит: цифры 0 и 1
Базис: последовательность чисел Фибоначчи 1, 2, 3, 5, 8, 13, 21, 34, …
Факториальная система счисления
Алфавит: количество цифр увеличивается с ростом номера разряда
Базис: 1!, 2!, 3!, …
Позиционные
системы счисления (ПСС)

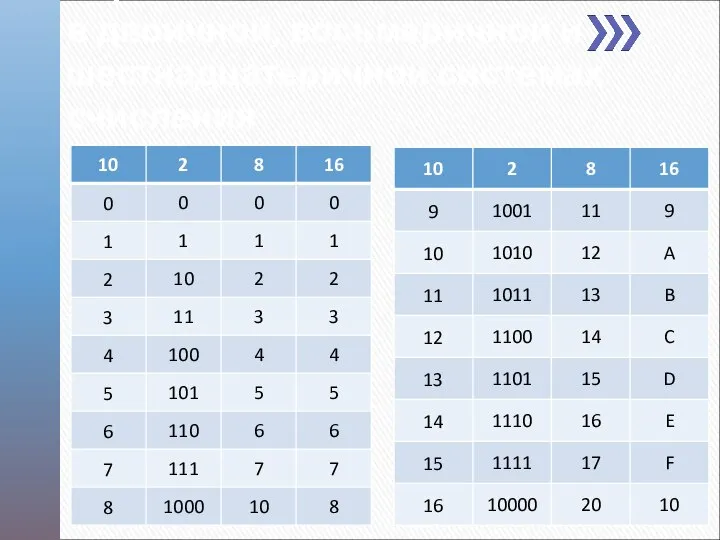
Первые числа
в двоичной, восьмеричной и шестнадцатеричной системах счисления

Сложение
Вычитание
Умножение
Деление
(действуют обычные правила выполнения операций «в столбик», подробнее рассмотрим в следующей лекции)
Арифметические
операции в ПСС