Слайд 2Рекуррентная последовательность
Числовая последовательность {xk} называется рекуррентной ранга p, если
где a0, a1,

…, ap – 1 – константы, а f – функция
Слайд 3Пример рекуррентной последовательности

Слайд 4Примеры тестов
Тесты по методу черного ящика:
минимально возможное n=0
на 1 больше минимально возможного,

n=1
другое значение n, например, n=6
Тесты по методу белого ящика:
такое n, чтобы цикл ни разу не выполнялся, n=0
такое n, чтобы цикл выполнился 1 раз, n=1
несколько большее значение n, например, n=6
Т.е. все тесты: n=0, n=1, n=6
На выходе, соответственно: F=1, F=1, F=720
Слайд 5Трудоемкость алгоритма
Элементарный шаг – это действие, время выполнения которого не зависит от

числа входных переменных и их значений, например:
один или фиксированное число выполняемых подряд операторов присваивания
проверка условия в условном операторе или цикле
вызов функции и возврат из функции
Слайд 6Трудоемкость алгоритма
Трудоемкость – это функция зависимости количества элементарных действий от входного параметра

n при n→∞.
Например, для цикла, который выполняется n раз, трудоемкость T(n) = A·n + B. Здесь коэффициент B – это число шагов до первой проверки условия, а A – число элементарных шагов при однократном выполнении цикла.
Коэффициенты зависят от компьютера и качества трансляции, поэтому на практике важно не точное значение, а порядок роста T(n) при n →∞. В нашем случае T(n) растет линейно относительно n, и это обозначается в виде: T(n) = O(n)
Слайд 7Числа Фибоначчи
Числа Фибоначчи задаются рекуррентной последовательностью ранга 2:
int n, f0, f1, f2,

k; cin >> n;
f0 = 0; f1 = 1;
for (k = 2; k <= n; k++)
{
f2 = f0 + f1; f0 = f1; f1 = f2;
}
Слайд 9Приближенное вычисление предела последовательности
Последовательность может иметь предел при n → ∞. Например, некоторый конечный

предел может иметь последовательность сумм
где слагаемые fk стремятся к нулю при k → ∞.
Слайд 10Приближенное вычисление предела последовательности
double eps, a, f, S;
int k;
cin >>

a >> eps;
k = 1; S = f = a;
while (abs(f) >= eps)
{
k++;
f = p(k, f);
S += f;
}
Слайд 11Приближенное значение функции sin x
Рекуррентное соотношение для элементов суммы:

Слайд 12Алгоритм вычисления sin x
double eps, x, f, S;
int k; cin >>

x >> eps;
k = 1; S = f = x;
while (abs(f) >= eps)
{
k++;
f = -f*x*x/(2*k-1)/(2*k-2);
S += f;
}
Количество k выполнений цикла:
если |x| ≤ 1, ε ≤ 1/2, то k ≤ log2 1/ε
Слайд 13Рекуррентная последовательность Герона
Можно доказать, что при a ≥ 0.













 Технология создания видеороликов посредством специализированных программ и их публикации в сети интернет
Технология создания видеороликов посредством специализированных программ и их публикации в сети интернет Электронные таблицы. Основные параметры электронных таблиц
Электронные таблицы. Основные параметры электронных таблиц Создание новостного текста
Создание новостного текста Отслеживание ошибок. Методы предотвращения ошибок во время разработки
Отслеживание ошибок. Методы предотвращения ошибок во время разработки Региональный проект Антитеррор
Региональный проект Антитеррор Леттеринг и его применение
Леттеринг и его применение Архитектура и применение системы энергоменеджмента EcoStruxure
Архитектура и применение системы энергоменеджмента EcoStruxure Операционные системы
Операционные системы Примеры использования внешних устройств, подключаемых к компьютеру, в учебных целях. Программное обеспечение внешних устройств
Примеры использования внешних устройств, подключаемых к компьютеру, в учебных целях. Программное обеспечение внешних устройств Макровирус
Макровирус Экономический факультет
Экономический факультет Реляционное исчисление кортежей. Система запросов
Реляционное исчисление кортежей. Система запросов 3ds max. Базовые уроки
3ds max. Базовые уроки Программирование на языке Паскаль
Программирование на языке Паскаль 9-1_Компьютерные сети
9-1_Компьютерные сети Создание презентаций. Викторина
Создание презентаций. Викторина Создание тематической презентации
Создание тематической презентации Администрирование информационных систем
Администрирование информационных систем Windows 10. Linux Subsystem
Windows 10. Linux Subsystem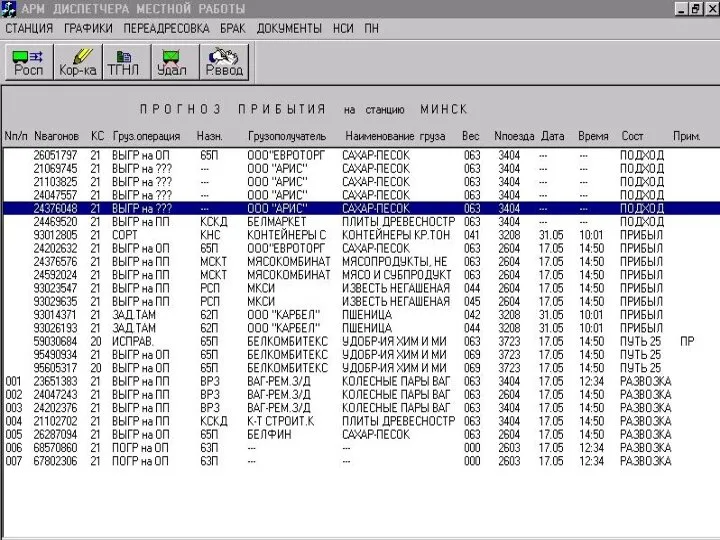 Описание и работа автоматизированной системы управления сортировочной станцией. Формы АРМ ДСЦМ
Описание и работа автоматизированной системы управления сортировочной станцией. Формы АРМ ДСЦМ Photoshop. Знакомство
Photoshop. Знакомство Информация и информационные ресурсы
Информация и информационные ресурсы Правила техники безопасности в компьютерном классе
Правила техники безопасности в компьютерном классе Информация и информационные процессы. Ключевые слова
Информация и информационные процессы. Ключевые слова Защита информации в интернете. Проведение финансовых операций с использованием Интернета
Защита информации в интернете. Проведение финансовых операций с использованием Интернета Системное программное обеспечение
Системное программное обеспечение Языки для записи алгоритмов
Языки для записи алгоритмов Информационные технологии в психологии. Анализ Интернет-ресурсов
Информационные технологии в психологии. Анализ Интернет-ресурсов