Слайд 2Основні властивості ЗЛП і теореми лінійного програмування
1. Застосування класичного апарату математичного аналізу

для вирішення ЗЛП
2. Теорема про оптимальність вершини багатогранника
3. Базисні розв’язки
4. Теореми ЛП
Теорема «ДБР↔вершина»
Фундаментальна теорема
Теорема про скінченність множини ДБР ЗЛП
Теорема про скінченність координат ДБР
Слайд 3Існування глобального розв’язку

Слайд 4Існування глобального розв’язку

Слайд 7
Величина постійна і не залежить від точки обчислення

Слайд 8Теорема про оптимальність вершини багатогранника

Слайд 9Теорема про оптимальність вершини багатогранника
Доведення частини І: «максимум у вершині»

Слайд 10Теорема про оптимальність вершини багатогранника.
Доведення частини І: «максимум у вершині»

Слайд 11Теорема про оптимальність вершини багатогранника.
Доведення частини І: «максимум у вершині»

Слайд 12Теорема про оптимальність вершини багатогранника
Доведення частини І: «максимум у вершині»

Слайд 13Теорема про оптимальність вершини багатогранника
Доведення частини І: «максимум у вершині»

Слайд 14Теорема про оптимальність вершини багатогранника
Доведення частини ІІ

Слайд 15Базисні розв’язки
(Алгебраїчне представлення вершин)
ЗЛП:
ЗЛП в КФ

Слайд 16Базисні розв’язки
(Алгебраїчне представлення вершин)
Кожну точку цієї множини можна визначити за допомогою шести
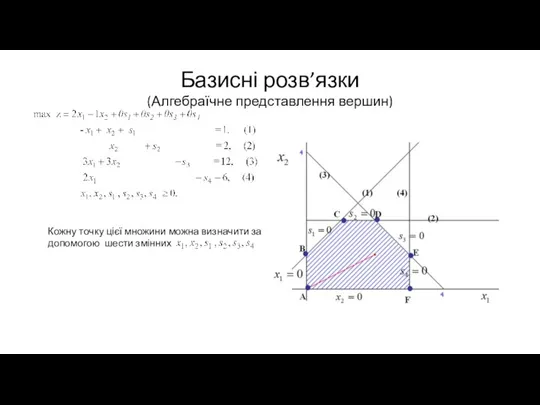
змінних
Слайд 17Базисні розв’язки
(Алгебраїчне представлення вершин)
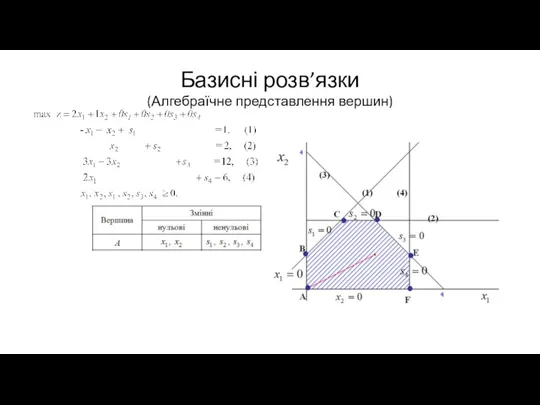
Слайд 18Базисні розв’язки
(Алгебраїчне представлення вершин)
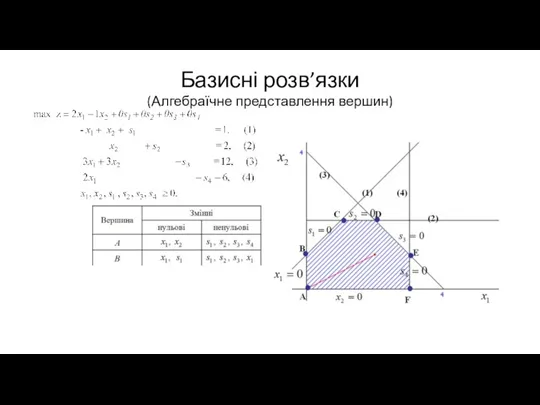
Слайд 19Базисні розв’язки
(Алгебраїчне представлення вершин)
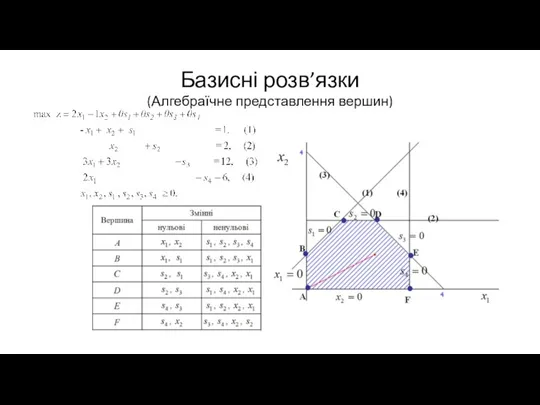
Слайд 20Базисні розв’язки
(Алгебраїчне представлення вершин)
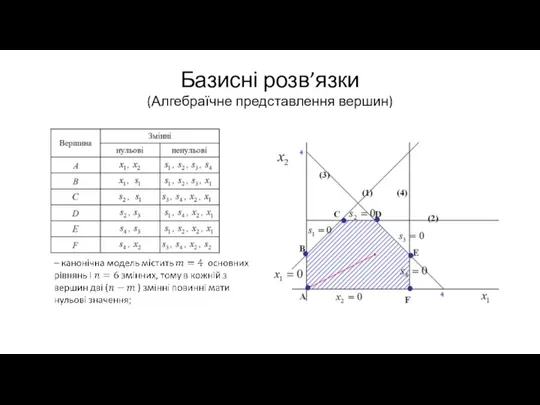
Слайд 21Базисні розв’язки
(Алгебраїчне представлення вершин)
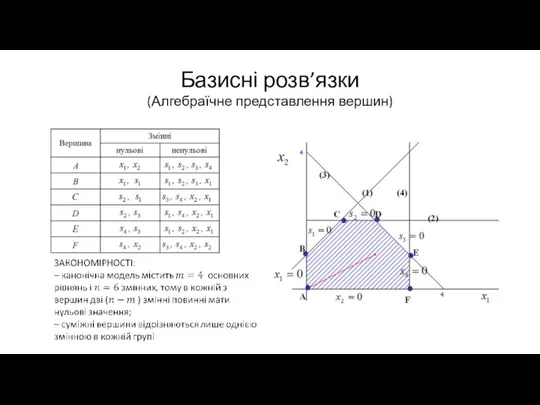
Слайд 22Базисні розв’язки
(Алгебраїчне представлення вершин)
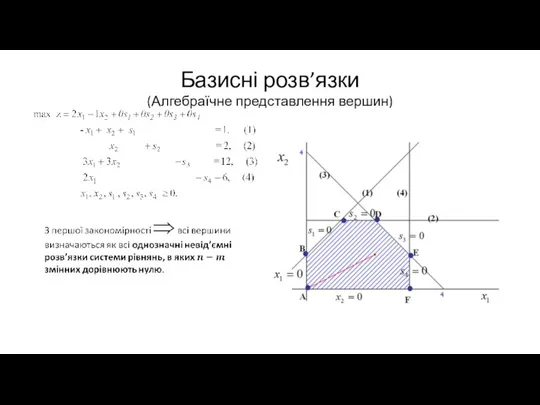
Слайд 23Базисні розв’язки
(Алгебраїчне представлення вершин)
Щоб система мала єдиний розв’язок, стовпці матриці обмежень повинні
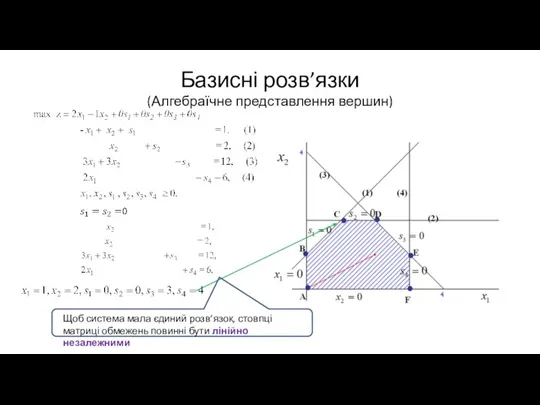
бути лінійно незалежними
Слайд 24Базисні розв’язки
(Алгебраїчне представлення вершин)

Слайд 25Базисні розв’язки
(Алгебраїчне представлення вершин)

Слайд 26Процедура знаходження базисних розв’язків (БР)

Слайд 27Допустимі базисні розв’язки (ДБР)

Слайд 28Приклад екзаменаційного завдання (0)
Чи є базисом наступні множини векторів?
Якщо так, то

знайти відповідний базисний розв’язок.
Чи є він допустимим?
Слайд 29Приклад екзаменаційного завдання (1)
ДБР
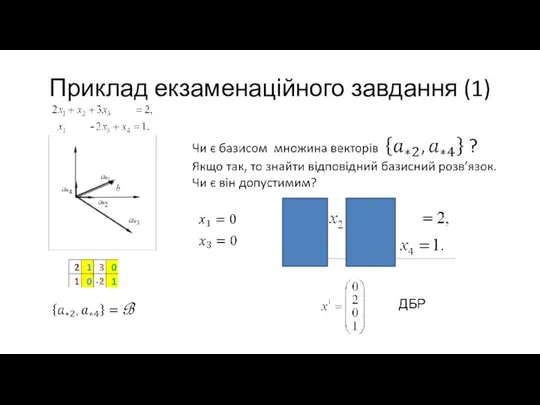
Слайд 30Приклад екзаменаційного завдання (2)
БР не допустимий
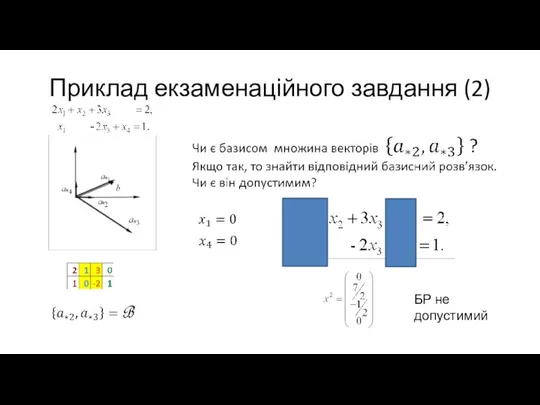
Слайд 31Приклад екзаменаційного завдання (3)

Слайд 32Приклад екзаменаційного завдання (4)

Слайд 33Приклад екзаменаційного завдання (5)

Слайд 37Теорема (фундаментальна)
Якщо ЗЛП має оптимальний розв’язок (у обмеженій області завжди, а

в необмеженій – залежно від обмеженості цільової функції), то він збігається, принаймні, з одним з ДБР системи обмежень.
Слайд 38Теорема про скінченність множини ДБР ЗЛП

Слайд 39Теорема про скінченність множини ДБР ЗЛП

Слайд 40БР vs ДБР vs Вершини (екз.завдання)
Яка кількість БР, ДБР, вершин?
БР: 26 ДБР:
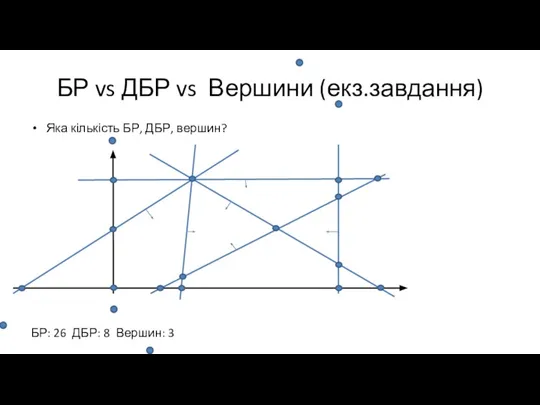
8 Вершин: 3
Слайд 41Теорема про скінченність координат ДБР
(Довести самостійно №)

Слайд 42Приклад екзаменаційного завдання
Знайти верхню межу компонентів ДБР ЗЛП:










































 Локальная и глобальная сеть
Локальная и глобальная сеть Создание слайдов с триггерами
Создание слайдов с триггерами Получение и визуализация данных
Получение и визуализация данных Способы записи алгоритмов
Способы записи алгоритмов Компьютерные вирусы
Компьютерные вирусы Структуры и алгоритмы компьютерной обработки данных
Структуры и алгоритмы компьютерной обработки данных Логобук. Что включает в себя логобук?
Логобук. Что включает в себя логобук? Восстановление данных
Восстановление данных Архивация данных
Архивация данных Топология сетей (продолжение). Занятие 04
Топология сетей (продолжение). Занятие 04 Основы Python. Составные типы данных. Функции. Область видимости переменных
Основы Python. Составные типы данных. Функции. Область видимости переменных Хранение информационных объектов различных видов на различных цифровых носителях
Хранение информационных объектов различных видов на различных цифровых носителях Как продлить займ
Как продлить займ Презентация на тему Создание визитной карточки
Презентация на тему Создание визитной карточки  Итилиум. Введение
Итилиум. Введение Combi Air Campaign Messaging approach INSIGHT
Combi Air Campaign Messaging approach INSIGHT Компьютерная графика
Компьютерная графика Компьютерные технологии в системе сельской техники
Компьютерные технологии в системе сельской техники Разработка Python-приложения для построения графиков математических функций
Разработка Python-приложения для построения графиков математических функций Использование компьютера в сфере Торговля
Использование компьютера в сфере Торговля Презентация на тему Адресация и передача информации в сети Интернет
Презентация на тему Адресация и передача информации в сети Интернет  Весёлые звуки
Весёлые звуки Поиск профессионально значимой информации в сети интернет
Поиск профессионально значимой информации в сети интернет ИТ автоматизации офиса
ИТ автоматизации офиса Защита детей от информации, причиняющей вред их здоровью и развитию
Защита детей от информации, причиняющей вред их здоровью и развитию Алгоритмизация и программирование
Алгоритмизация и программирование Виды конечных элементов, способы нанесения сетки. Виды анализа конструкций
Виды конечных элементов, способы нанесения сетки. Виды анализа конструкций Билеты 7-9
Билеты 7-9