Системы счисления. Тема 2.3.1. Свойства позиционной записи числа: количество цифр в записи, признак делимости числа

даёт представления множества чисел (целых и/или вещественных);
даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление);
отражает алгебраическую и арифметическую структуру чисел.
Систе́ма счисле́ния— символический метод записи чисел, представление чисел с помощью письменных знаков.

Позиционные
Непозиционные
Смешанные
Системы счисления

один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен.
В позиционных системах чем больше основание системы счисления, тем меньшее количество разрядов (то есть записываемых цифр) требуется при записи числа
Позиционная система счисления

2 — двоичная (в дискретной математике, информатике, программировании);
3 — троичная;
8 — восьмеричная;
10 — десятичная (используется повсеместно);
12 — двенадцатеричная (счёт дюжинами);
16 — шестнадцатеричная (используется в программировании, информатике);
20 — двадцатеричная;
60 — шестидесятеричная (единицы измерения времени, измерение углов и, в частности, координат, долготы и широты).
Наиболее часто употребляемыми в настоящее время позиционными системами являются:

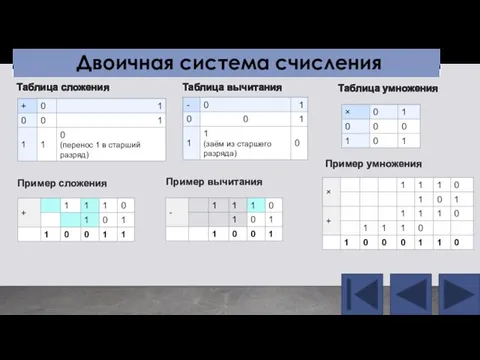
Двоичная система счисления
Таблица сложения
Таблица вычитания
Пример сложения
Пример вычитания
Таблица умножения
Пример умножения

позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.
Чаще всего используется в областях, связанных с цифровыми устройствами.
Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных. Широко использовалась в программировании и компьютерной документации, однако позднее была почти полностью вытеснена шестнадцатеричной.
Восьмери́чная систе́ма счисле́ния

Позиционная система счисления по целочисленному основанию 16.
В качестве цифр этой системы счисления обычно используются цифры от 0 до 9 и латинские буквы от A до F.
Буквы A, B, C, D, E, F имеют значения 1010, 1110, 1210, 1310, 1410, 1510 соответственно.
Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной адресуемой единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами.
Шестнадцатеричная система счисления

Является обобщением b-ичной системы счисления и также зачастую относится к позиционным системам счисления. Основанием смешанной системы
счисления является возрастающая последовательность чисел , и
каждое число X в ней представляется как линейная комбинация:
где на коэффициенты ak, называемые как и прежде цифрами,
накладываются некоторые ограничения.
Примеры: Факториальная и Фибоначчиева системы счисления
Смешанная система счисления

В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе.
При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.
ПРИМЕРЫ
Биномиальная система счисления
Система остаточных классов (СОК)
Система счисления Штерна-Броко
Непозиционные системы счисления