Паскаль_ЧислМетоды

Численные методы (язык Паскаль)
Тема 1. Решение уравнений
© К.Ю. Поляков, 2008-2009

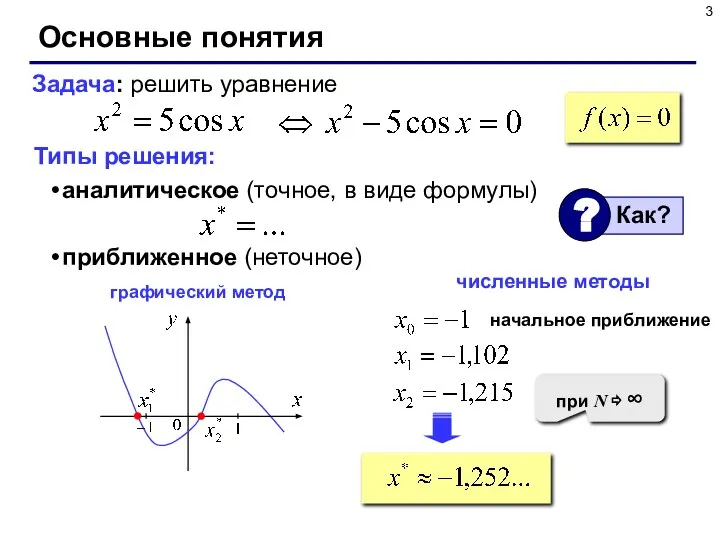
Основные понятия
Типы решения:
аналитическое (точное, в виде формулы)
приближенное (неточное)
Задача: решить уравнение
численные методы
начальное приближение
при N ⇨ ∞

Численные методы
Идея: последовательное уточнение решения с помощью некоторого алгоритма.
Область применения: когда найти точное решение невозможно или крайне сложно.
можно найти хоть какое-то решение
во многих случаях можно оценить ошибку (то есть можно найти решение с заданной точностью)
нельзя найти точное решение
невозможно исследовать решение при изменении параметров
большой объем вычислений
иногда сложно оценить ошибку
нет универсальных методов

Есть ли решение на [a, b]?
есть решение
нет решения
нет решения

Метод дихотомии (деление пополам)
Найти середину отрезка [a,b]: c = (a + b) / 2;
Если f(c)*f(a)<0, сдвинуть правую границу интервала b = c;
Если f(c)*f(a)≥ 0, сдвинуть левую границу интервала a = c;
Повторять шаги 1-3, пока не будет b – a ≤ ε.

Метод дихотомии (деления пополам)
простота
можно получить решение с заданной точностью (в пределах точности машинных вычислений)
нужно знать интервал [a, b]
на интервале [a, b] должно быть только одно решение
большое число шагов для достижения высокой точности
только для функций одной переменной

Метод деления отрезка пополам
{----------------------------------------------
BinSolve находит решение на [a,b]
методом деления отрезка пополам
Вход: a, b - границы интервала, a < b
eps - точность решения
Выход: x - решение уравнения f(x)=0
----------------------------------------------}
function BinSolve (a, b, eps: real): real;
var c:real;
begin
while b - a > eps do begin
c := (a + b) / 2;
if f(a)*f(c) < 0 then
b := c
else a := c;
end;
BinSolve := (a + b) / 2;
end;
function f(x:real): real;
begin
f := x*x – 5;
end;

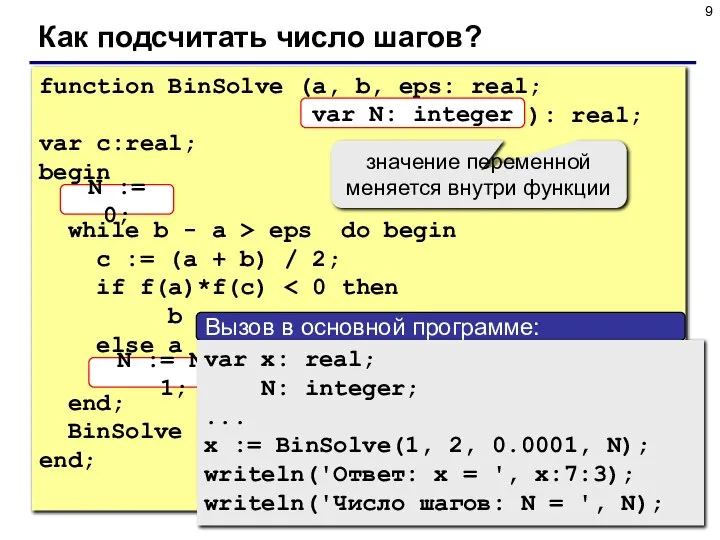
Как подсчитать число шагов?
function BinSolve (a, b, eps: real;
var N: integer ): real;
var c:real;
begin
N := 0;
while b - a > eps do begin
c := (a + b) / 2;
if f(a)*f(c) < 0 then
b := c
else a := c;
N := N + 1;
end;
BinSolve := (a + b) / 2;
end;
var N: integer
N := 0;
N := N + 1;
значение переменной меняется внутри функции

Метод итераций (повторений)
Задача:
Эквивалентные преобразования:
имеет те же решения при
Идея решения:
– начальное приближение (например, с графика)
Проблемы:
как лучше выбрать ?
всегда ли так можно найти решение?

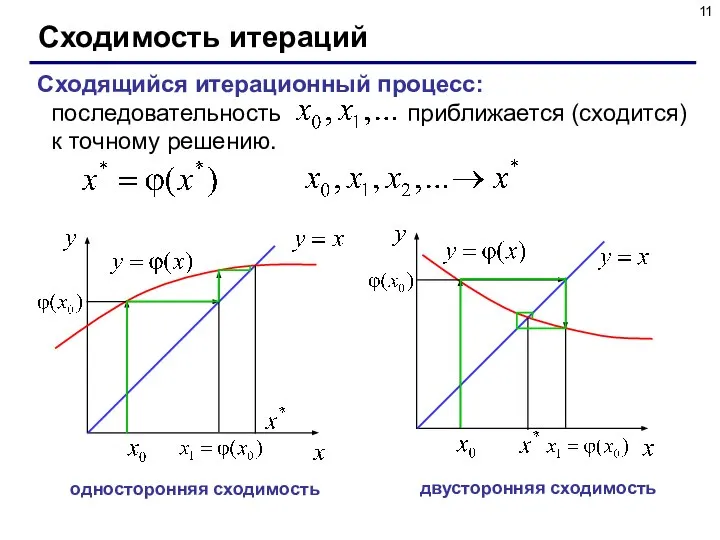
Сходимость итераций
Сходящийся итерационный процесс: последовательность приближается (сходится) к точному решению.
односторонняя сходимость
двусторонняя сходимость

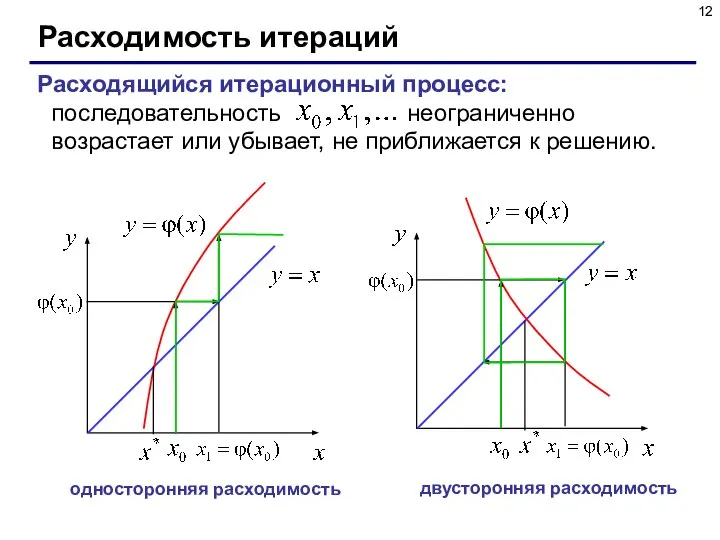
Расходимость итераций
Расходящийся итерационный процесс: последовательность неограниченно возрастает или убывает, не приближается к решению.
односторонняя расходимость
двусторонняя расходимость

От чего зависит сходимость?
сходится
расходится
Выводы:
сходимость итераций зависит от производной
итерации сходятся при и расходятся при
сходимость определяется выбором параметра b

Как выбрать b?
наугад, пробовать разные варианты
для начального приближения x0
пересчитывать на каждом шаге, например:

Метод итераций (программа)
{----------------------------------------------
Iter решение уравнения методом итераций
Вход: x – начальное приближение
b – параметр
eps - точность решения
Выход: решение уравнения f(x)=0, n - число шагов
----------------------------------------------}
function Iter (x, b, eps: real; var N: integer): real;
var dx: real;
OK: boolean;
begin
N := 0;
OK := False; {еще не нашли}
while not OK and (N < 100) do begin
dx := b*f(x);
x := x + dx;
N := N + 1;
if abs(dx) < eps then OK := True;
end;
Iter := x;
end;
аварийный выход
(итерации расходятся)
нормальный выход

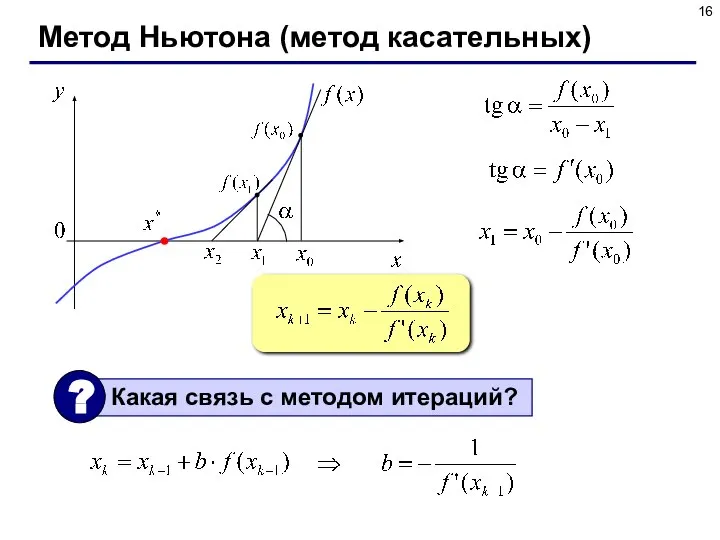
Метод Ньютона (метод касательных)

Метод Ньютона (программа)
{----------------------------------------------
Newton решение уравнения методом Ньютона
Вход: x – начальное приближение
eps - точность решения
Выход: решение уравнения f(x)=0, n - число шагов
----------------------------------------------}
function Newton (x, eps: real; var N: integer): real;
var dx: real;
OK: boolean;
begin
N := 0; OK := False;
while not OK and (N < 100) do
begin
dx := f(x) / df(x);
x := x - dx;
N := N + 1;
OK := abs(dx) < eps;
end;
Newton := x;
end;
{ функция }
function f(x:real): real;
begin
f := 3*x*x*x+2*x+5;
end;
{ производная }
function df(x:real): real;
begin
df := 9*x*x + 2;
end;

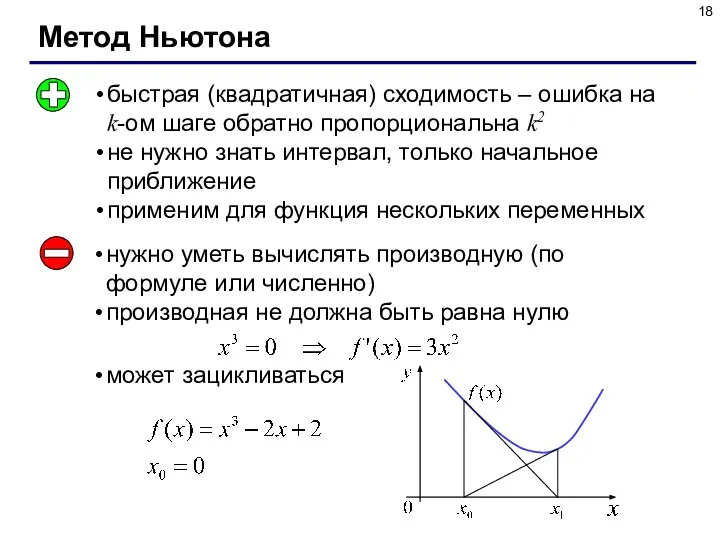
Метод Ньютона
быстрая (квадратичная) сходимость – ошибка на k-ом шаге обратно пропорциональна k2
не нужно знать интервал, только начальное приближение
применим для функция нескольких переменных
нужно уметь вычислять производную (по формуле или численно)
производная не должна быть равна нулю
может зацикливаться

Численные методы (язык Паскаль)
Тема 2. Вычисление площади
(интеграла)
© К.Ю. Поляков, 2008-2009

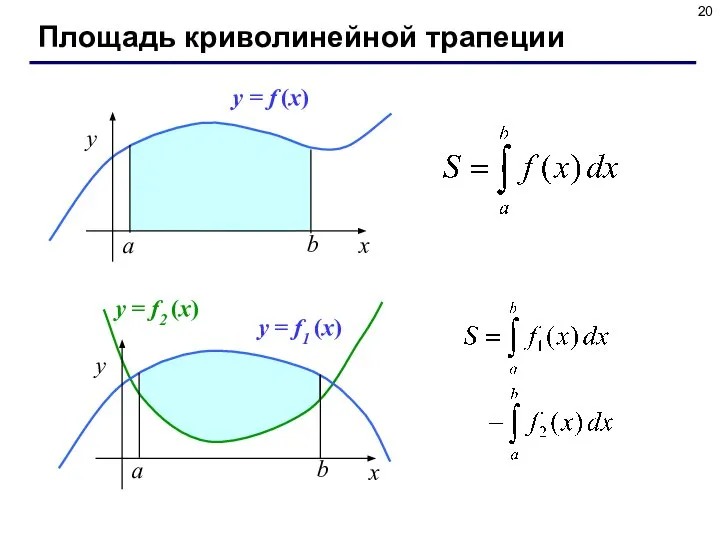
Площадь криволинейной трапеции

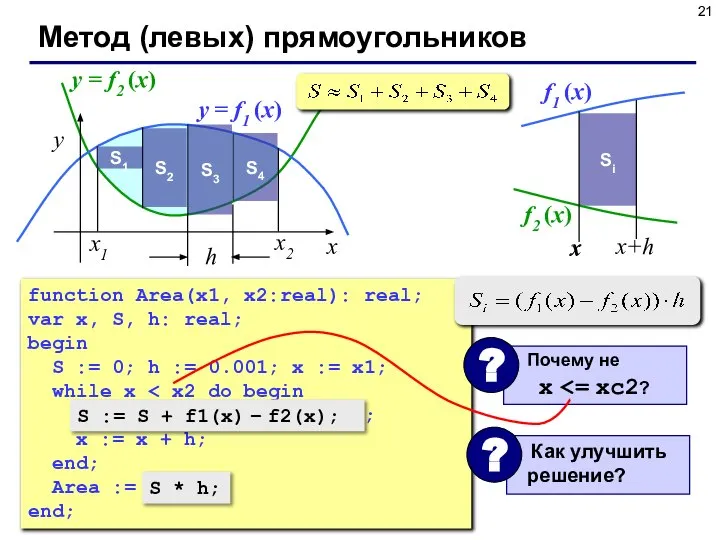
function Area(x1, x2:real): real;
var x, S, h: real;
begin
S := 0; h := 0.001; x := x1;
while x < x2 do begin
S := S + h*(f1(x)-f2(x));
x := x + h;
end;
Area := S;
end;
Метод (левых) прямоугольников
y = f1 (x)
y = f2 (x)
S1
S2
S3
S4
S * h;
S := S + f1(x) – f2(x);

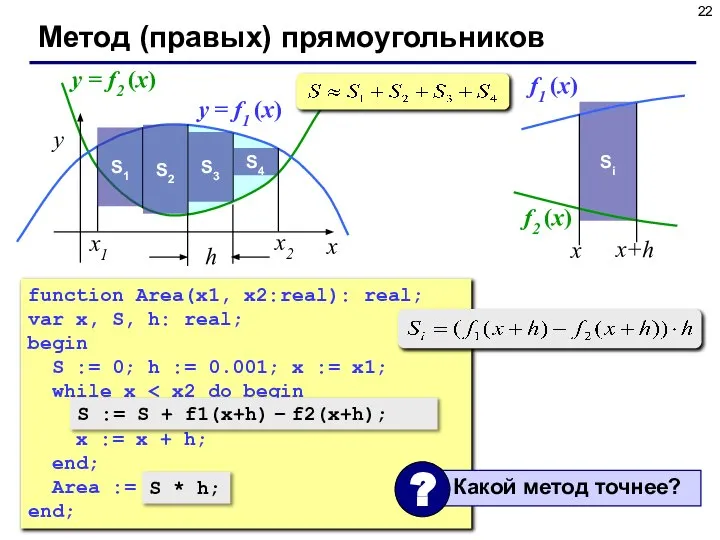
Метод (правых) прямоугольников
x
y
x2
x1
y = f1 (x)
y = f2 (x)
S1
S2
S3
S4
function Area(x1, x2:real): real;
var x, S, h: real;
begin
S := 0; h := 0.001; x := x1;
while x < x2 do begin
S := S + h*(f1(x+h)-f2(x+h));
x := x + h;
end;
Area := S;
end;
S * h;
S := S + f1(x+h) – f2(x+h);

function Area(x1, x2:real): real;
var x, S, h: real;
begin
S := 0; h := 0.001; x := x1;
while x < x2 do begin
S := S + f1(x+h/2) – f2(x+h/2);
x := x + h;
end;
Area := S*h;
end;
Метод (средних) прямоугольников
x
y
x2
x1
y = f1 (x)
y = f2 (x)
S1
S2
S3
S4
левые (правые):
средние

x = x1;
while x < x2 do begin
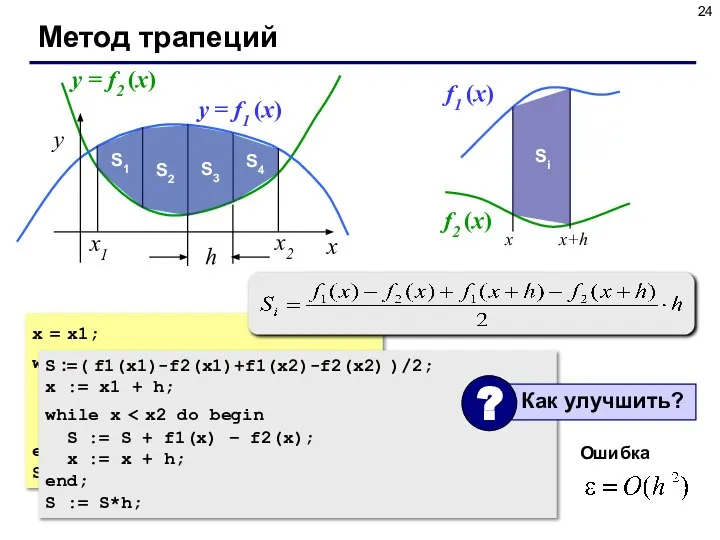
S:= S + f1(x) – f2(x)
+ f1(x+h) – f2(x+h);
x:= x + h;
end;
S := S*h/2;
Метод трапеций
x
y
x2
x1
y = f1 (x)
y = f2 (x)
S :=( f1(x1)-f2(x1)+f1(x2)-f2(x2) )/2;
x := x1 + h;
while x < x2 do begin
S := S + f1(x) – f2(x);
x := x + h;
end;
S := S*h;

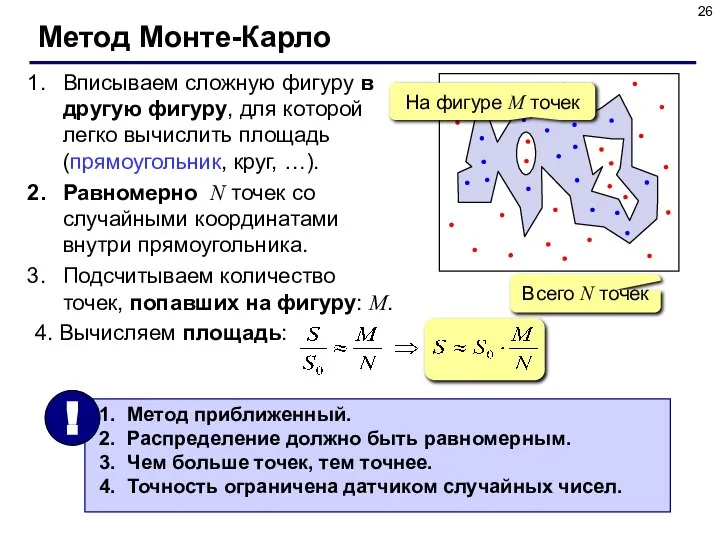
Метод Монте-Карло
Применение: вычисление площадей сложных фигур (трудно применить другие методы).
Требования: необходимо уметь достаточно просто определять, попала ли точка (x, y) внутрь фигуры.
Пример: заданы 100 кругов (координаты центра, радиусы), которые могу пересекаться. Найти площадь области, перекрытой кругами.

Метод Монте-Карло
Вписываем сложную фигуру в другую фигуру, для которой легко вычислить площадь (прямоугольник, круг, …).
Равномерно N точек со случайными координатами внутри прямоугольника.
Подсчитываем количество точек, попавших на фигуру: M.
4. Вычисляем площадь:
Всего N точек
На фигуре M точек
Метод приближенный.
Распределение должно быть равномерным.
Чем больше точек, тем точнее.
Точность ограничена датчиком случайных чисел.
!

Численные методы (язык Паскаль)
Тема 3. Вычисление длины кривой
© К.Ю. Поляков, 2008-2009

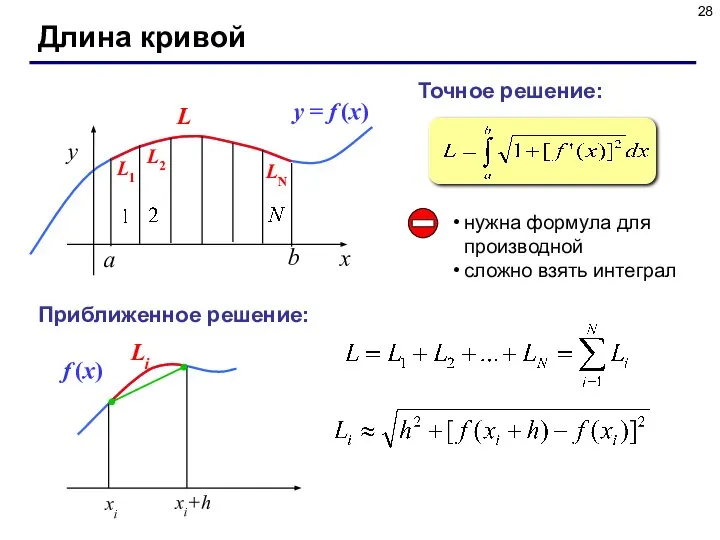
Длина кривой
Точное решение:
нужна формула для производной
сложно взять интеграл
Приближенное решение:

Длина кривой
{----------------------------------------------
CurveLen вычисление длины кривой
Вход: a, b – границы интервала Выход: длина кривой y = f(x) на интервале [a,b]
----------------------------------------------}
function CurveLen(a, b: real): real;
var x, dy, h, L: real;
begin
h := 0.001; L := 0;
x := a;
while x < b do begin
dy := f(x+h) - f(x);
L := L + sqrt(h*h + dy*dy);
x := x + h;
end;
CurveLen := L;
end;

Численные методы
Тема 4. Оптимизация
© К.Ю. Поляков, 2008-2009

Найти x, при котором или при заданных ограничениях.
Основные понятия
Оптимизация – поиск оптимального (наилучшего в некотором смысле) решения.
Цель: определить значения неизвестных параметров, при которых заданная функция достигает минимума (затраты) или максимума (доходы).
Ограничения – условия, которые делают задачу осмысленной.
или

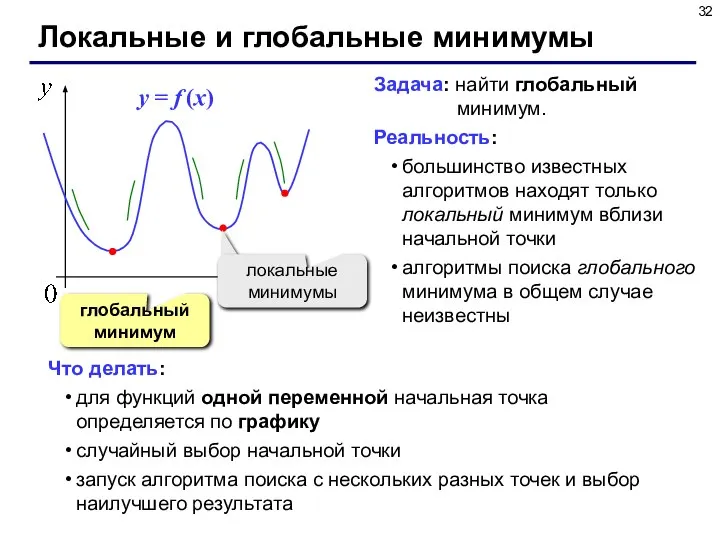
Локальные и глобальные минимумы
глобальный минимум
Задача: найти глобальный минимум.
Реальность:
большинство известных алгоритмов находят только локальный минимум вблизи начальной точки
алгоритмы поиска глобального минимума в общем случае неизвестны
Что делать:
для функций одной переменной начальная точка определяется по графику
случайный выбор начальной точки
запуск алгоритма поиска с нескольких разных точек и выбор наилучшего результата

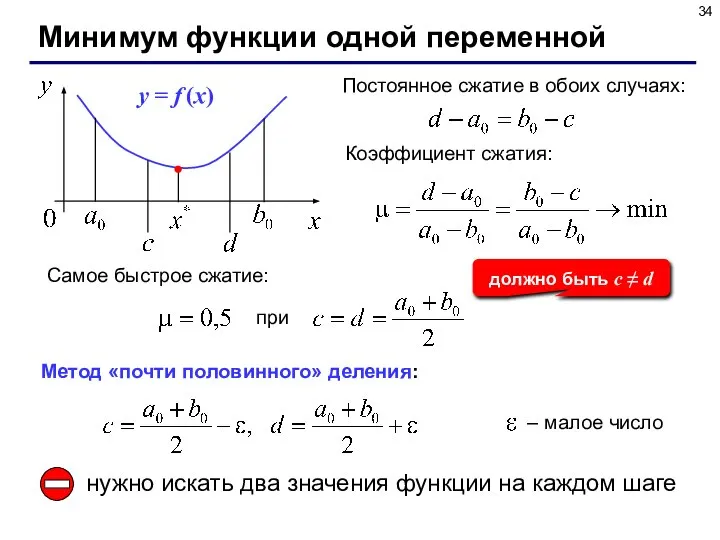
Минимум функции одной переменной
Дано: на интервале [a,b] функция непрерывна и имеет единственный минимум.
Найти: x*
y = f (x)
Принцип сжатия интервала:

Минимум функции одной переменной
Коэффициент сжатия:
Самое быстрое сжатие:
при
должно быть c ≠ d
Метод «почти половинного» деления:
– малое число
нужно искать два значения функции на каждом шаге

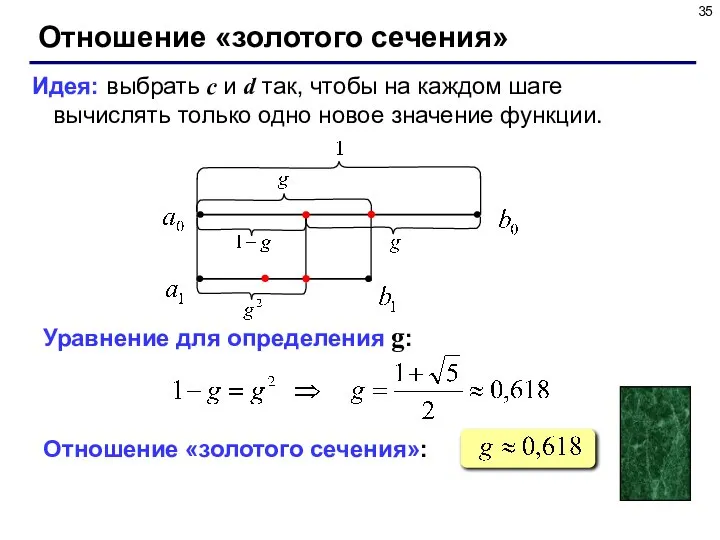
Отношение «золотого сечения»
Идея: выбрать c и d так, чтобы на каждом шаге вычислять только одно новое значение функции.
Уравнение для определения g:
Отношение «золотого сечения»:

Метод «золотого сечения»
{----------------------------------------------
Gold поиск минимума функции («золотое сечение»)
Вход: a, b – границы интервала, eps – точность
Выход: x, при котором f(x) имеет минимум на [a,b]
----------------------------------------------}
function Gold(a, b, eps:real): real;
const g = 0.618034;
var x1, x2, R: real;
begin
R := g*(b - a);
while abs(b-a) > eps do begin
x1 := b - R; x2 := a + R;
if f(x1) > f(x2) then a := x1
else b := x2;
R := R * g;
end;
Gold := (a + b) / 2;
end;

Функции нескольких переменных
Проблемы:
нет универсальных алгоритмов поиска глобального минимума
неясно, как выбрать начальное приближение (зависит от задачи и интуиции)
Подходы:
методы локальной оптимизации (результат зависит от выбора начального приближения)
случайный поиск (без гарантии)
методы глобальной оптимизации (для особых классов функций)

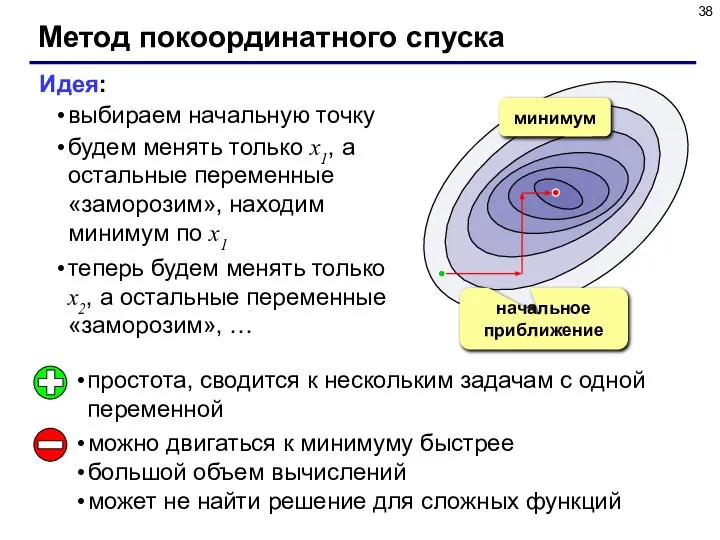
Метод покоординатного спуска
Идея:
выбираем начальную точку
будем менять только x1, а остальные переменные «заморозим», находим минимум по x1
теперь будем менять только x2, а остальные переменные «заморозим», …
начальное приближение
минимум
простота, сводится к нескольким задачам с одной переменной
можно двигаться к минимуму быстрее
большой объем вычислений
может не найти решение для сложных функций

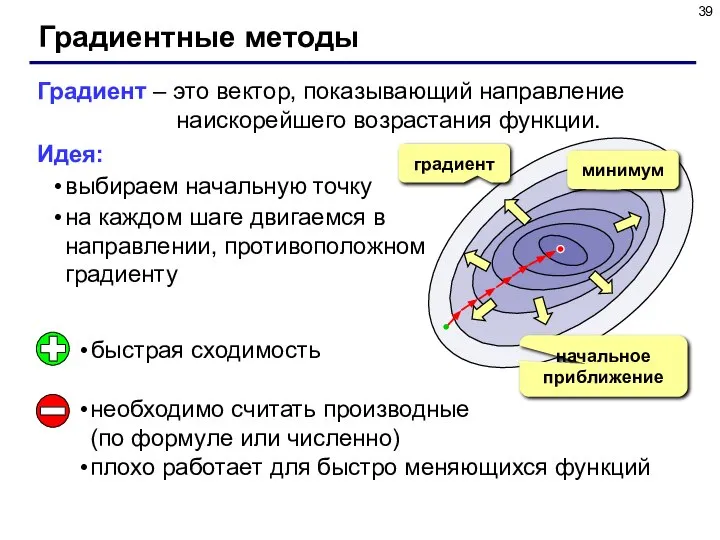
Градиентные методы
Градиент – это вектор, показывающий направление наискорейшего возрастания функции.
Идея:
выбираем начальную точку
на каждом шаге двигаемся в
направлении, противоположном
градиенту
минимум
начальное приближение
быстрая сходимость
необходимо считать производные
(по формуле или численно)
плохо работает для быстро меняющихся функций
градиент

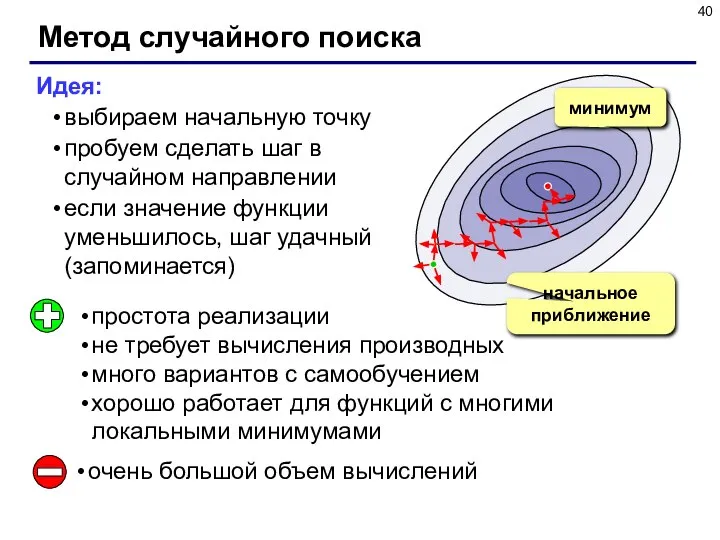
Метод случайного поиска
Идея:
выбираем начальную точку
пробуем сделать шаг в случайном направлении
если значение функции уменьшилось, шаг удачный (запоминается)
минимум
начальное приближение
простота реализации
не требует вычисления производных
много вариантов с самообучением
хорошо работает для функций с многими локальными минимумами
очень большой объем вычислений