- Главная
- Информатика
- ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ ПОЗИЦИОННОЙ СИСТЕМЫ В ДРУГУЮ

Содержание
- 2. Перевод целого десятичного числа в систему счисления с оcнованием q Для перевода целого десятичного числа в
- 3. Вопросы и задания № 1. 1310 = Х2 = 11012 44 22 11 5 0 0
- 4. Перевод целого десятичного числа в двоичную систему счисления Для перевода числа Х (X≤10000) в двоичную систему
- 6. Скачать презентацию
Слайд 2Перевод целого десятичного числа в систему счисления с оcнованием q
Для перевода целого
Перевод целого десятичного числа в систему счисления с оcнованием q
Для перевода целого

десятичного числа в систему счисления с основанием q следует:
последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, равное нулю;
полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления;
составить число в новой системе счисления, записывая его, начиная с последнего остатка.
последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, равное нулю;
полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления;
составить число в новой системе счисления, записывая его, начиная с последнего остатка.
Слайд 3Вопросы и задания
№ 1. 1310 = Х2
= 11012
44
22
11
5
0
0
1
1
№ 2. 4410 =
Вопросы и задания
№ 1. 1310 = Х2
= 11012
44
22
11
5
0
0
1
1
№ 2. 4410 =

Х2
= 1011002
2
0
1
1
№ 3. 17210 = Х8
= 2548
№ 4. 17210 = Х16
= АС16
Слайд 4Перевод целого десятичного числа в двоичную систему счисления
Для перевода числа Х (X≤10000)
Перевод целого десятичного числа в двоичную систему счисления
Для перевода числа Х (X≤10000)

в двоичную систему счисления можно воспользоваться таблицей степеней двойки.
№ 6. 52910 = Х2
= 10000100012
Решение:
Представим число в виде суммы степеней двойки, для этого:
52910 = 512
512 + 16 + 1 =
= 29 + 24 + 20
= 10000100012
возьмем максимально возможное значение, не превы-шающее исходное число (512 < 529);
найдем разность между исходным числом и этим значением (17);
выпишем степень двойки, не превышающее эту разность
и т. д.
+ 17 =
- Предыдущая
Эффективная коммуникацияСледующая -
Средневековая философия. Лекция №6 Анализ неструктурированных данных и оптимизация их хранения
Анализ неструктурированных данных и оптимизация их хранения Маршрутизация и транспортировка данных по компьютерным сетям
Маршрутизация и транспортировка данных по компьютерным сетям Data centre services in Estonia
Data centre services in Estonia Основы языка HTML. Язык разметки гипертекста
Основы языка HTML. Язык разметки гипертекста Алгоритмы электронной подписи. Схема Эль-Гамаля
Алгоритмы электронной подписи. Схема Эль-Гамаля Проект онлайн турнира по CS:GO “Cyber stalker”
Проект онлайн турнира по CS:GO “Cyber stalker” Правила безопасного поведения в Интернете
Правила безопасного поведения в Интернете Alwar. Анотація аудіо
Alwar. Анотація аудіо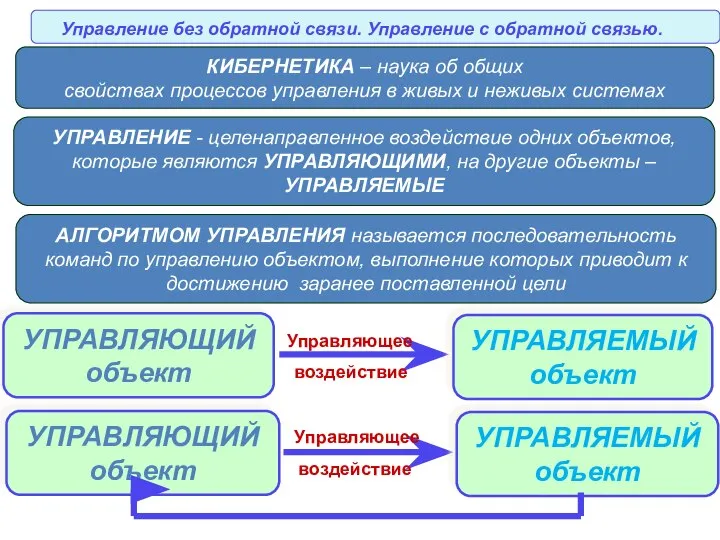 3. Определения и свойства алгоритмов. Типы алгоритмов
3. Определения и свойства алгоритмов. Типы алгоритмов СМИ и НКО
СМИ и НКО Кто такой копирайтер
Кто такой копирайтер ВКР: Автоматизация документооборота организации
ВКР: Автоматизация документооборота организации Презентация на тему Музыкальный оператор Play
Презентация на тему Музыкальный оператор Play  Беспроводные компьютерные сети
Беспроводные компьютерные сети Тестирование ПО. Уровень 1. Тестировщик программного обеспечения
Тестирование ПО. Уровень 1. Тестировщик программного обеспечения Устройство компьютера
Устройство компьютера Виртуальная экскурсия. Основные преимущества и недостатки
Виртуальная экскурсия. Основные преимущества и недостатки Решение задач с циклом
Решение задач с циклом Рисование вазы в графическом редакторе Paint
Рисование вазы в графическом редакторе Paint Виртуальный мир
Виртуальный мир Нам нужно перейти на BIM!
Нам нужно перейти на BIM! World Wide Web
World Wide Web Алгоритм это выполнения команд последовательность
Алгоритм это выполнения команд последовательность Создание презентаций с помощью MS PowerPoint
Создание презентаций с помощью MS PowerPoint Этапы создания презентации
Этапы создания презентации Тестирование методом черного ящика
Тестирование методом черного ящика Машинное обучение. День 3. Регрессия
Машинное обучение. День 3. Регрессия Портал Школьное Питание. Электронный учет оплаты питания учащихся
Портал Школьное Питание. Электронный учет оплаты питания учащихся