Перевод чисел из одной позиционной системы в другую. Представление информации в компьютере

Ключевые слова
система счисления
триада
тетрада
«компьютерные» системы счисления
«быстрый» перевод

Перевод целого десятичного числа в систему счисления с оcнованием q
Для перевода целого десятичного числа в систему счисления с основанием q следует:
последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, равное нулю;
полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления;
составить число в новой системе счисления, записывая его, начиная с последнего остатка.

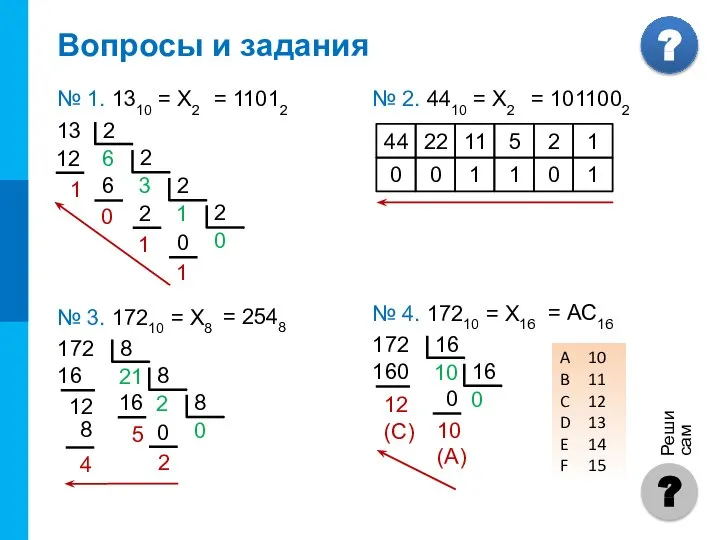
Вопросы и задания
№ 1. 1310 = Х2
= 11012
44
22
11
5
0
0
1
1
№ 2. 4410 = Х2
= 1011002
2
0
1
1
№ 3. 17210 = Х8
= 2548
№ 4. 17210 = Х16
= АС16
?
Реши сам

Решите самостоятельно
ОТВЕТ
№ 5. Переведите десятичные числа в указанные системы счисления.
а) 10010 = X2
б) 18710 = X8
в) 257210 = X16
г) 145810 = X5
д) 5310 = X3
= 11001002
= 2738
= A0C16
= 213135
= 12223
е) 23310 = X2
ж) 30210 = X8
з) 380210 = X16
и) 95010 = X5
к) 4110 = X3
= 111010012
= 4568
= EDA16
= 123005
= 11123

Перевод целого десятичного числа в двоичную систему счисления
Для перевода числа Х (X≤10000) в двоичную систему счисле-ния можно воспользоваться таблицей степеней двойки.
№ 6. 52910 = Х2
= 10000100012
Решение:
Представим число в виде суммы степеней двойки, для этого:
52910 = 512
512 + 16 + 1 =
= 29 + 24 + 20
= 10000100012
?
Реши сам
возьмем максимально возможное значение, не превы-шающее исходное число (512 < 529);
найдем разность между исходным числом и этим значением (17);
выпишем степень двойки, не превышающее эту разность
и т. д.
+ 17 =

Решите самостоятельно
ОТВЕТ
№ 7. Переведите десятичные числа в двоичную систему счисления, используя таблицу степеней двойки:
а) 9710 = X2
б) 32810 = X2
в) 109010 = X2
= 1100 0012
= 1010010002
= 100010000102
г) 8410 = X2
д) 29210 = X2
е) 54710 = X2
= 10101002
= 1001001002
= 10001000112

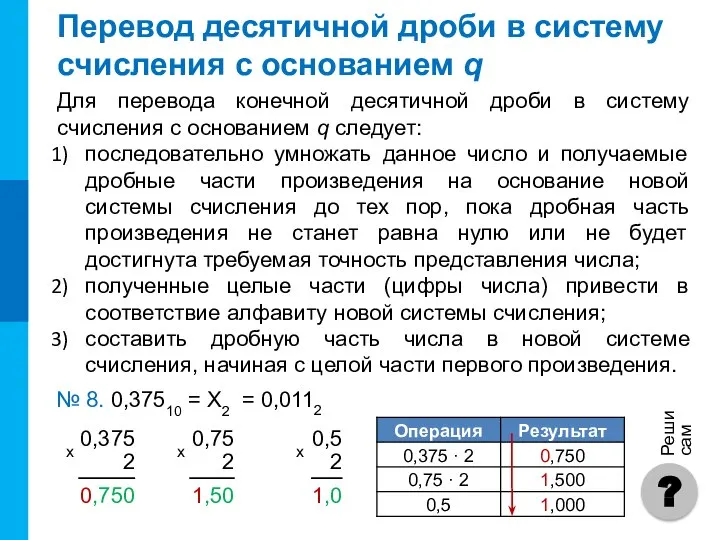
Перевод десятичной дроби в систему счисления с основанием q
Для перевода конечной десятичной дроби в систему счисления с основанием q следует:
последовательно умножать данное число и получаемые дробные части произведения на основание новой системы счисления до тех пор, пока дробная часть произведения не станет равна нулю или не будет достигнута требуемая точность представления числа;
полученные целые части (цифры числа) привести в соответствие алфавиту новой системы счисления;
составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
№ 8. 0,37510 = Х2
= 0,0112
0,375
2
0,750
х
0,75
2
1,50
х
0,5
2
1,0
х
?
Реши сам

Решите самостоятельно
ОТВЕТ
№ 9. Переведите десятичные дроби в систему счисления с указанным основанием (с точностью до трех знаков после запятой):
а) 0,62510 = X2
б) 0,24510 = X8
в) 0,46010 = X16
= 0,1012
= 0,1758
= 0,75С16
г) 0,75010 = X2
д) 0,12510 = X8
е) 0,36510 = X16
= 0,1102
= 0,1008
= 0,5D716

Решите самостоятельно
ОТВЕТ
№ 10. Переведите смешанные десятичные числа в систему счисления с указанным основанием (с точностью до трех знаков после запятой):
а) 98,7510 = X2
б) 100,37510 = X8
в) 121,12110 = X16
= 1100010,1102
= 144,3008
≈ 79,1EF16
г) 43,12510 = X2
д) 16,7810 = X8
е) 750,75010 = X16
= 101011,0012
≈ 20,6178
= 2EE,C0016
При переводе смешанных чисел из десятичной системы счисления в любую другую отдельно (по разным правилам) переводится целая и дробная части.

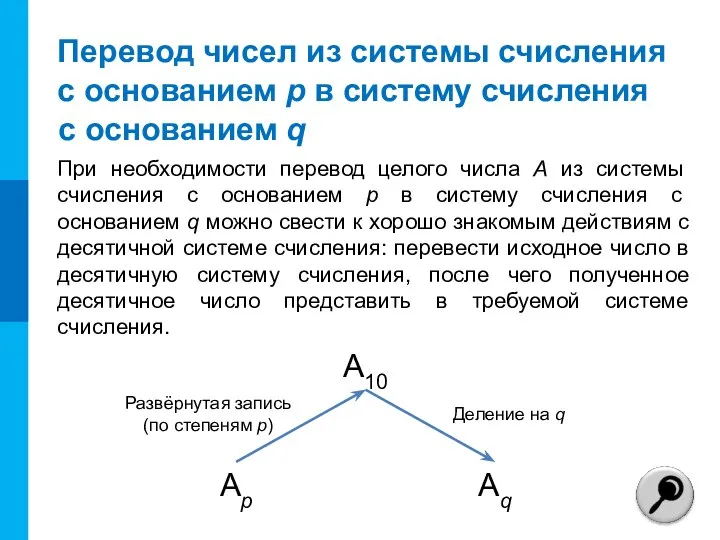
Перевод чисел из системы счисления с основанием р в систему счисления
При необходимости перевод целого числа А из системы счисления с основанием p в систему счисления с основанием q можно свести к хорошо знакомым действиям с десятичной системе счисления: перевести исходное число в десятичную систему счисления, после чего полученное десятичное число представить в требуемой системе счисления.
А10
Аp
Аq
Развёрнутая запись
(по степеням p)
Деление на q
с основанием q

Перевод целых чисел из системы
счисления с основанием р в систему счисления с основанием q
Все действия производятся в исходной системе счисления p.
Делим число и полученные неполные частные на основание другой системы счисления до тех пор, пока неполное частное не станет равным нулю. Полученную в ходе деления последовательность остатков записываем в обратном порядке.
Пример. 135 = Х3
= 223
Все действия производим в 5-ной системе счисления.
Проверка:
135 = 1 · 5 + 3 = 810
223 = 2 · 3 + 2 = 810

Перевод чисел из системы
счисления с основанием р в систему
счисления с основанием q
1. Записать исходное число в развернутой форме:
an · pn + an-1 · pn-1 + ... + a1 · p1 + a0 · p0 ,
где p - старое основание.
2. Произвести вычисления в новой системе счисления q.
Пример. 213 = Х5
= 125
Все действия производим в 5-ной системе счисления.
Проверка:
213 = 2 · 3 + 1 = 710
125 = 1 · 5 + 2 = 710
2 · 3 + 1 · 30
= 11 + 1 = 125

Способ «быстрого» перевода основан на том, что каждой цифре числа в системе счисления, основание которой q кратно степени двойки, соответствует число, состоящее из n (q=2n) цифр в двоичной системе счисления. Замена восьмеричных цифр двоичными тройками (триадами) и шестнадцатеричных цифр двоичными четвёрками (тетра-дами) позволяет осуществлять быстрый перевод. Для этого:
данное двоичное число надо разбить справа налево на группы по n цифр в каждой;
если в последней левой группе окажется меньше n разрядов, то её надо дополнить слева нулями до нужного числа разрядов;
рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой системы счисления с основанием q = 2n.
Быстрый перевод чисел в компьютерных системах счисления
Способ «быстрого» перевода основан на том, что каждой цифре числа в системе счисления, основание которой q кратно степени двойки, соответствует число, состоящее из n (q=2n) цифр в двоичной системе счисления. Замена восьмеричных цифр двоичными тройками (триадами) и шестнадцатеричных цифр двоичными четвёрками (тетра-дами) позволяет осуществлять быстрый перевод.

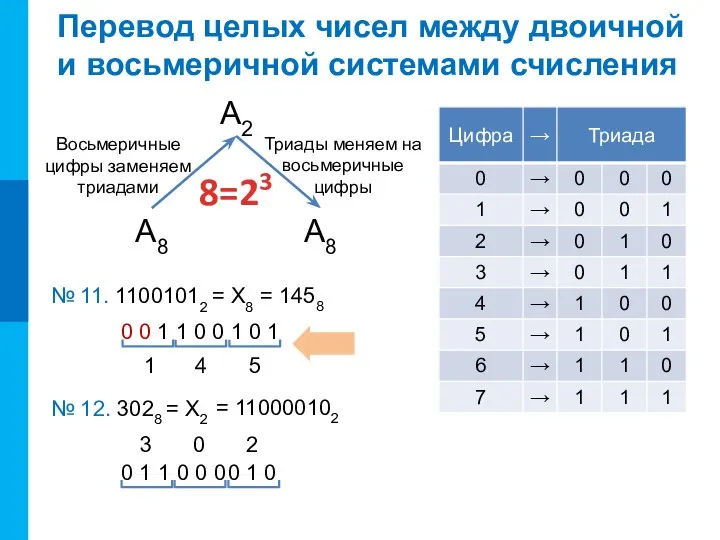
8=23
Перевод целых чисел между двоичной и восьмеричной системами счисления
А2
А8
А8
Восьмеричные цифры заменяем триадами
Триады меняем на восьмеричные цифры
№ 11. 11001012 = Х8
= 1458
1
4
5
№ 12. 3028 = Х2
= 110000102
0 1 1
0 0 0
0 1 0
0 0 1 1 0 0 1 0 1

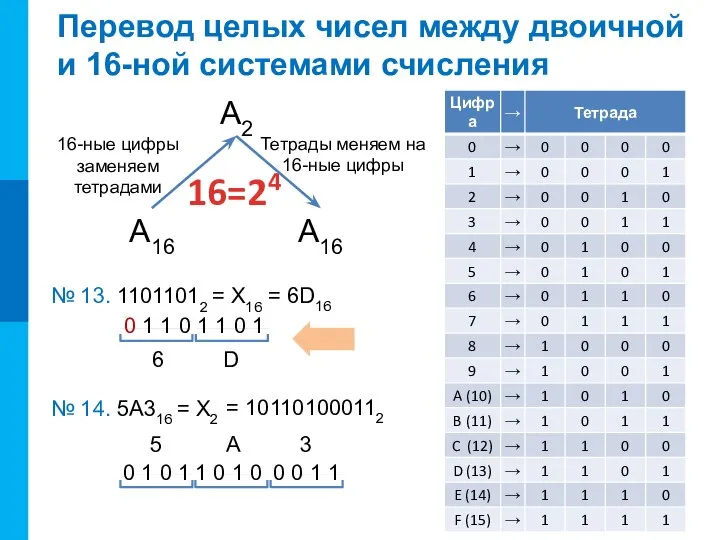
0 1 0 1
1 0 1 0
0 0 1 1
16=24
Перевод целых чисел между двоичной и 16-ной системами счисления
А2
А16
А16
16-ные цифры заменяем
тетрадами
Тетрады меняем на
16-ные цифры
№ 13. 11011012 = Х16
= 6D16
6
D
№ 14. 5A316 = Х2
= 101101000112
0 1 1 0 1 1 0 1

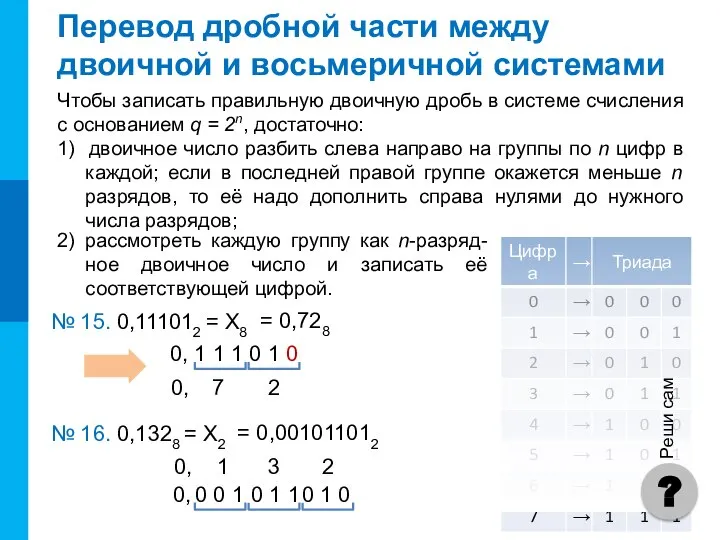
Перевод дробной части между двоичной и восьмеричной системами
№ 15. 0,111012 = Х8
= 0,728
7
2
№ 16. 0,1328 = Х2
= 0,001011012
0 0 1
0 1 1
0 1 0
0, 1 1 1 0 1 0
Чтобы записать правильную двоичную дробь в системе счисления с основанием q = 2n, достаточно:
1) двоичное число разбить слева направо на группы по n цифр в каждой; если в последней правой группе окажется меньше n разрядов, то её надо дополнить справа нулями до нужного числа разрядов;
2) рассмотреть каждую группу как n-разряд-ное двоичное число и записать её соответствующей цифрой.
0,
0,
Реши сам
?

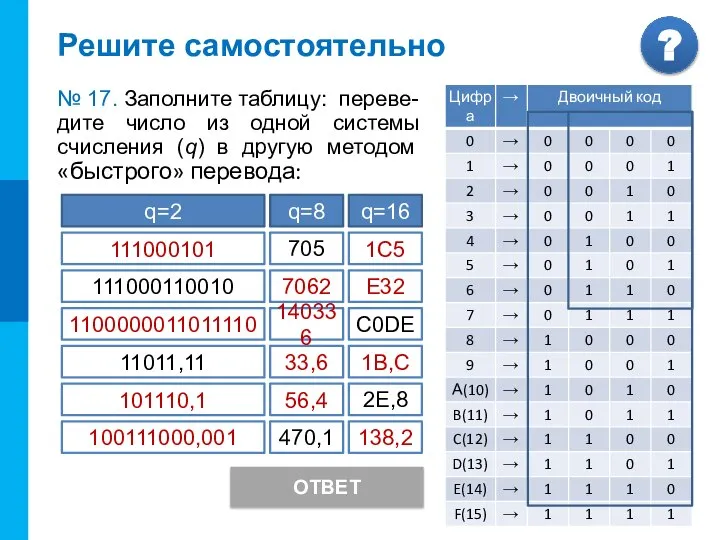
Решите самостоятельно
№ 17. Заполните таблицу: переве-дите число из одной системы счисления (q) в другую методом «быстрого» перевода:
ОТВЕТ

Самое главное
Для перевода целого десятичного числа в систему счисления с основанием q следует:
последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, равное нулю;
полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления;
составить число в новой системе счисления, записывая его, начиная с последнего остатка.

Самое главное
В компьютерных науках широко используются двоичная, восьмеричная и шестнадцатеричная системы счисления, поэтому их называют «компьютерными». Между основания-ми этих систем существует очевидная связь: 16 = 24, 8 = 23.
Если основание системы счисления q кратно степени двойки (q = 2n), то любое число в этой системе счисления можно «быстро» перевести в двоичную систему счисления, выписав последовательно двоичные коды каждой из цифр, образующих исходное число. Замена восьмеричных цифр двоичными тройками (триадами) и шестнадцатеричных цифр двоичными четвёрками (тетрадами) позволяет осуществлять быстрый перевод между этими системами счисления, не прибегая к арифметическим операциям.

Вопросы и задания
Задание 1. Укажите через запятую в порядке убывания все основания систем счисления, в которых запись десятичного числа 33 оканчивается на 5.
Решение:
Поскольку запись числа в системе счисления с основанием q заканчивается на 5, то остаток от деления числа 33 на q равен пяти: 33 mod q = 5.
Следовательно, (33-5) mod q = 0, т.е. 28 mod q =0.
Это верно для q ∈ {28, 14, 7, 4, 2, 1}.
Так как в новой системе счисления запись числа оканчивается на пять, то q > 5.
Следовательно, условию задачи удовлетворяют основания: 28, 14 и 7.
Ответ: 28, 14 и 7.

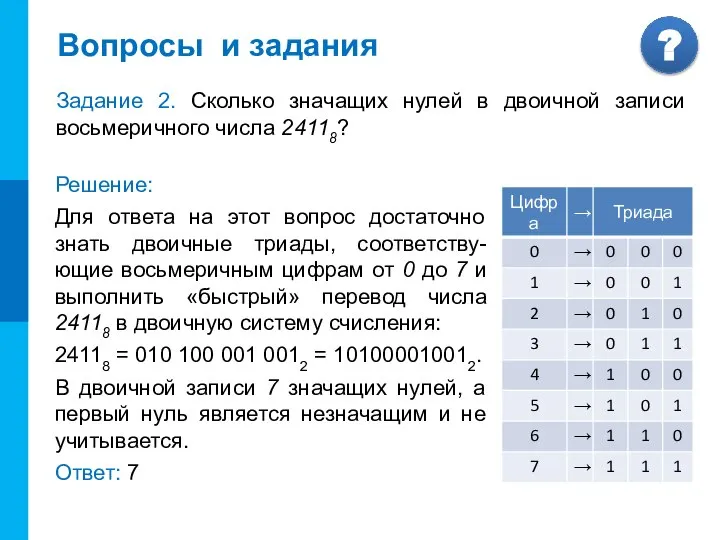
Вопросы и задания
Задание 2. Сколько значащих нулей в двоичной записи восьмеричного числа 24118?
Решение:
Для ответа на этот вопрос достаточно знать двоичные триады, соответству-ющие восьмеричным цифрам от 0 до 7 и выполнить «быстрый» перевод числа 24118 в двоичную систему счисления:
24118 = 010 100 001 0012 = 101000010012.
В двоичной записи 7 значащих нулей, а первый нуль является незначащим и не учитывается.
Ответ: 7

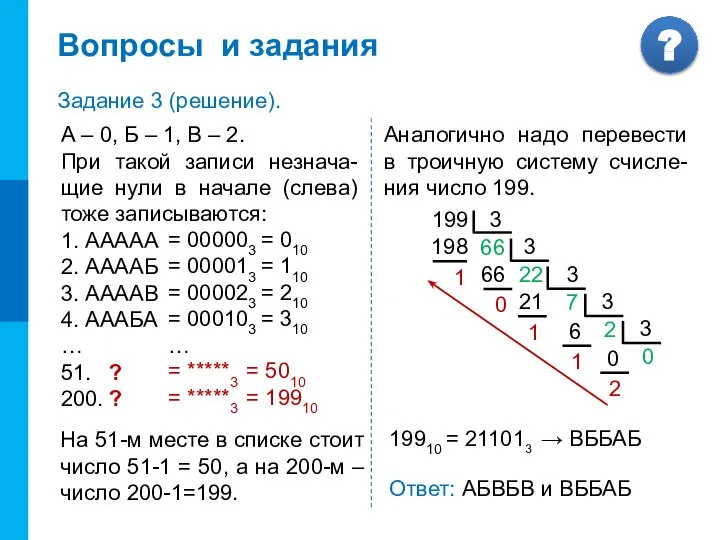
Вопросы и задания
Задание 3. Все 5-буквенные слова, составленные из букв
А, Б и В, записаны в алфавитном порядке и пронумеро-ваны. Вот начало списка:
1. ААААА
2. ААААБ
3. ААААВ
4. АААБА
5. АААББ
…
Какие слова находятся в этом списке на 51-м и 200-м местах?
Решение:
Слово в трехбуквенном алфавите можно рассматривать, как запись слова в троичной системе в 5-разрядном представлении. Тогда А – 0, Б – 1, В – 2.

А – 0, Б – 1, В – 2.
При такой записи незнача-щие нули в начале (слева) тоже записываются:
1. ААААА
2. ААААБ
3. ААААВ
4. АААБА
…
51. ?
200. ?
Вопросы и задания
Задание 3 (решение).
= 000003 = 010
= 000013 = 110
= 000023 = 210
= 000103 = 310
…
Чтобы понять, какое слово соответствует этому числу, надо перевести его в троич-ную систему счисления и при необходимости дополнить слева «0» до пяти разрядов.
На 51-м месте в списке стоит число 51-1 = 50, а на 200-м – число 200-1=199.
→ АБВБВ
5010 = 012123
= *****3 = 5010
= *****3 = 19910
Аналогично надо перевести в троичную систему счисле-ния число 199.
→ ВББАБ
19910 = 211013
Ответ: АБВБВ и ВББАБ