Подсчёт количества программ. Задание

Задача 1

Задача 1
У исполнителя Калькулятор две команды, которым присвоены номера:
1. прибавь 1
2. умножь на 2
Сколько есть программ, которые число 1 преобразуют в число 16?

Решение задачи 1
Задача имеет два способа решения: подстановка и таблица.
Таблица – более простой и универсальный способ.
Мы разберём оба.

Решение задачи 1 – таблица
У исполнителя Калькулятор две команды, которым присвоены номера:
1. прибавь 1
2. умножь на 2
Сколько есть программ, которые число 1 преобразуют в число 16?
Составим таблицу, в котором будет две строки и 16 столбцов (т.к. мы работаем с числами от 1 до 16). Верхний ряд пронумеруем числами от 1 до 16.
Верхний ряд обозначает число, которое получает исполнитель,
а нижний ряд – количество программ, которые преобразуют 1 в это число.

Решение задачи 1 – таблица
Поставим 1 в первый столбец (существует одна программа, позволяющая из 1 получить 1 – это программа, в которой нет действий).
Если 1 уже получена, то 2 можно получить 2 способами:
1. 1 + 1
2. 1 * 2
Если двойка была получена первым способом, количество программ равно 1. Если двойка была получена вторым способом, количество программ тоже равно 1.
1 + 1 = 2 – количество программ для двойки.

Решение задачи 1 – таблица
Тройку можно получить только одним способом: к 2 прибавить 1 (т.к. нет такого целого числа, умножив которое на 2, можно получить 3).
Если есть две программы, которые дают 2, то и программ, которые дают 3, тоже всего две.
Четвёрку можно получить 2 способами:
1. 2 * 2
2. 3 + 1
Есть две программы, которые дают 2, и 2 программы, которые дают 3. Значит, существует 2 + 2 = 4 программы, которые дают 4.

Решение задачи 1 – таблица
Пятёрку можно получить только одним способом: 4 + 1 = 5. Количество программ для 4 равно четырём, значит, и для 5 существует всего 4 программы.
Шесть можно получить 2 способами:
1. 3 * 2
2. 5 + 1
Есть две программы, которые дают 3, и четыре программы, которые дают 5. Значит, существует 2 + 4 = 6 программ, которые дают 6.

Решение задачи 1 – таблица
Семь можно получить только одним способом: 6 + 1 = 7. Количество программ для 6 равно шести, значит, и для 7 существует всего шесть программы.
Восемь можно получить 2 способами:
1. 4 * 2
2. 7 + 1
Есть четыре программы, которые дают 4, и шесть программ, которые дают 7. Значит, существует 4 + 6 = 10 программ, которые дают 8.

Решение задачи 1 – таблица
Можно сделать следующий вывод: если K(N) – количество программ, которые дают число N, то
K(N) = K(N – 1), если N – нечётное число (см. разборы на предыдущих слайдах для чисел 3, 5, 7)
K(N) = K(N – 1) + K(N / 2), если N – чётное число (см. разборы на предыдущих слайдах для чисел 2, 4, 6, 8).
Поэтому для 9 количество программ K(9) = K(8) = 10
Для 10 количество программ K(10) = K(9) + K(5) = 10 + 4 = 14

Решение задачи 1 – таблица
И т.д. Заполним таблицу до конца:
Количество программ для 16 равно 36. Это и есть ответ.
Ответ: 36

Решение задачи 1 – подстановка
Это второй способ решения задачи.
Мы уже определили, что
если K(N) – количество программ,
которые дают число N, то
K(N) = K(N – 1), если N – нечётное число
K(N) = K(N – 1) + K(N / 2), если N – чётное число

Решение задачи 1 – подстановка
Получается, что:
K(16) = K(15) + K(8)
K(15) = K(14)
K(14) = K(13) + K(7)
K(13) = K(12)
K(12) = K(11) + K(6)
K(11) = K(10)
K(10) = K(9) + K(5)
K(9) = K(8)
K(8) = K(7) + K(4)
K(7) = K(6)
K(6) = K(5) + K(3)
K(5) = K(4)
K(4) = K(3) + K(2)
K(3) = K(2)
K(2) = K(1) + K(1)
K(1) = 1
Теперь подставим полученное значение в формулы.

Решение задачи 1 – подстановка
K(1) = 1
K(2) = K(1) + K(1) = 1 + 1 + 2
K(3) = K(2) = 2
K(4) = K(3) + K(2) = 2 + 2 = 4
K(5) = K(4) = 4
K(6) = K(5) + K(3) = 4 + 2 = 6
K(7) = K(6) = 6
K(8) = K(7) + K(4) = 6 + 4 = 10
K(9) = K(8) = 10
K(10) = K(9) + K(5) = 14
K(11) = K(10) = 14
K(12) = K(11) + K(6) = 20
K(13) = K(12) = 20
K(14) = K(13) + K(7) = 26
K(15) = K(14) = 26
K(16) = K(15) + K(8) = 36
Ответ: 36

Самостоятельно

Самостоятельно
1.1) У исполнителя Калькулятор две команды, которым присвоены номера:
1. прибавь 1
2. умножь на 4
Сколько есть программ, которые число 1 преобразуют в число 55?
1.2) У исполнителя Калькулятор две команды, которым присвоены номера:
1. прибавь 1
2. умножь на 4
Сколько есть программ, которые число 1 преобразуют в число 32?
1.3) У исполнителя Калькулятор две команды, которым присвоены номера:
1. прибавь 1
2. умножь на 3
Сколько есть программ, которые число 5 преобразуют в число 49?

Ответы
1.1) 32
1.2) 15
1.3) 15

Самостоятельно
1.4) У исполнителя Калькулятор три команды, которым присвоены номера:
1. прибавь 1
2. умножь на 2
3. умножь на 3
Сколько есть программ, которые число 1 преобразуют в число 18?
1.5) У исполнителя Калькулятор три команды, которым присвоены номера:
1. прибавь 1
2. прибавь 3
3. умножь на 2
Сколько есть программ, которые число 3 преобразуют в число 15?

Ответы
1.4) 96
1.5) 102

Задача 2

Задача 2
Исполнитель преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя Июнь15 – это последовательность команд. Сколько существует программ, для которых при исходном числе 1 результатом является число 21 и при этом траектория вычислений содержит число 10?

Решение задачи 2
Если в условии сказано, что траектория программы содержит
число X, то задачу нужно разбить на две:
определить количество программ, дающих Х, и
определить количество программ, из числа Х дающих требуемое конечное число.
По условию: исходное число – 1, результат – 21,
траектория содержит 10. ( 1→ 21 +10)
Следовательно, решаем 2 задачи:
исходное число – 1, результат – 10;
исходное число – 10, результат 21.

Решение задачи 2
1 часть решения: из 1 получаем 10.
K(N) = K(N – 1), если N – нечётное
K(N) = K(N – 1) + K(N / 2), если N – чётное
Решение с помощью таблицы:
Существует 14 программ, дающих число 10.

Решение задачи 2
2 часть решения: из 10 → 21.
K(N) = K(N – 1), если N – нечётное
K(N) = K(N – 1) + K(N / 2), если N – чётное
Но требуется учитывать, что число 10 дают 14 программ (а не 1)!
Ответ: 28

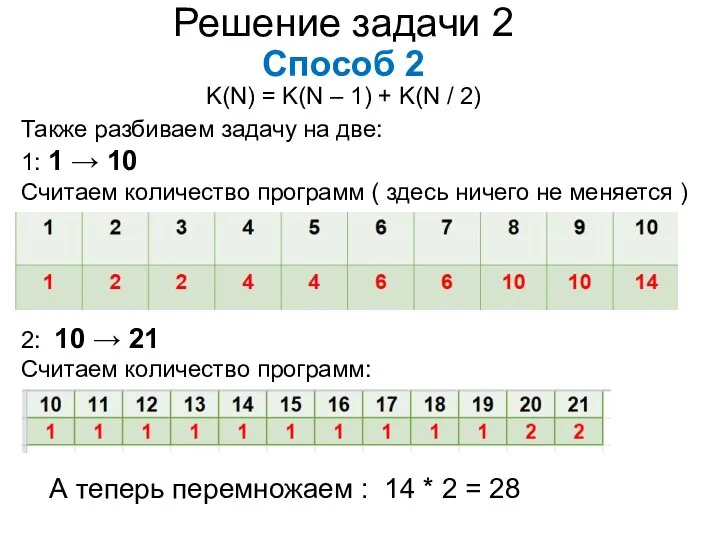
Решение задачи 2
Способ 2
K(N) = K(N – 1) + K(N / 2)
Также разбиваем задачу на две:
1: 1 → 10
Считаем количество программ ( здесь ничего не меняется )
2: 10 → 21
Считаем количество программ:
А теперь перемножаем : 14 * 2 = 28

Пример.
Исполнитель Калькулятор преобразует число, записанное на экране. У исполнителя есть команды, которым присвоены номера:
1. Прибавить 1,
2. Прибавить 5,
3. Умножить на 2.
Сколько существует программ, для которых при исходном числе 4 результатом является число 24 и при этом траектория содержит числа 11 и 18 ?
KN = KN – 1 + KN – 5 + KN / 2

KN = KN – 1 + KN – 5 + KN / 2
Решение примера (способ 2)
Разбиваем на три задачи:
Задача №1: 4 → 11
Задача №2: 11 → 18
Задача №3: 18 → 24
Перемножаем найденные результаты.
Задача №1: 4 → 11
Количество программ: 6

KN = KN – 1 + KN – 5 + KN / 2
Решение примера (способ 2)
Задача №2: 11 → 18
Количество программ: 4
Задача №3: 18 → 24
Количество программ: 3
Перемножаем полученные результаты: 6*4*3=72

Самостоятельно

Самостоятельно
2.1) Исполнитель Июнь15 преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя Июнь15 – это последовательность команд. Сколько существует программ, для которых при исходном числе 2 результатом является число 34 и при этом траектория вычислений содержит число 12?
2.2) Исполнитель Июнь16 преобразует число на экране. У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 2
3. Умножить на 2
Сколько существует программ, для которых при исходном числе 3 результатом является число 13 и при этом траектория вычислений содержит число 10?

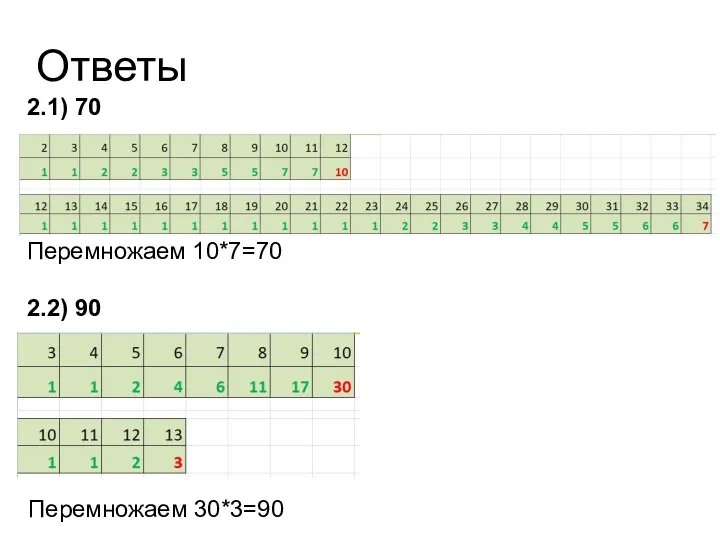
Ответы
2.1) 70
Перемножаем 10*7=70
2.2) 90
Перемножаем 30*3=90

Задача 3

Задача 3
Исполнитель Июнь16 преобразует число на экране. У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 2
3. Умножить на 2
Сколько существует программ, для которых при исходном числе 3 результатом является число 13 и при этом траектория вычислений не содержит число 8?

Решение задачи 3
Если в условии сказано, что траектория программы НЕ содержит число X, то:
1) при решении с помощью таблицы у Х ставим 0;
2) при решении подстановкой сразу пишем, что K(X) = 0.
Больше никаких отличий от обычного решения нет.

Решение задачи 3
Т.к. исполнитель имеет команды:
1. Прибавить 1
2. Прибавить 2
3. Умножить на 2
и траектория не содержит число 8, то:
K(1) = 1, K(2) = 1, K(8) = 0, для остальных чисел
K(N) = K(N – 1) + K(N – 2), если N – нечётное
K(N) = K(N – 1) + K(N – 2) + K(N / 2), если N – чётное
Решение с помощью таблицы:
Ответ: 40

Самостоятельно

Самостоятельно
3.1) Исполнитель Июнь16 преобразует число на экране. У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 2
3. Умножить на 2
Сколько существует программ, для которых при исходном числе 2 результатом является число 12 и при этом траектория вычислений не содержит число 10?
3.2) Исполнитель Июнь16 преобразует число на экране. У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 2
3. Умножить на 3
Сколько существует программ, для которых при исходном числе 2 результатом является число 16 и при этом траектория вычислений не содержит число 14?

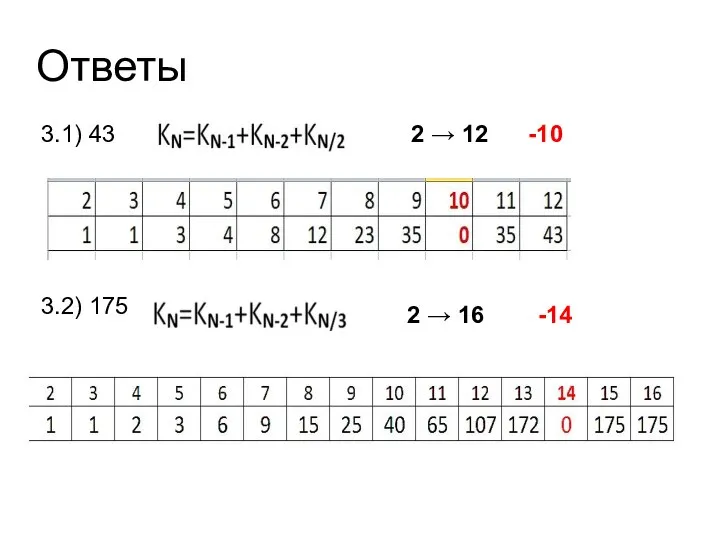
Ответы
3.1) 43
3.2) 175
2 → 12 -10
2 → 16 -14

Самостоятельно
4.1) Исполнитель R17 преобразует число, записанное на экране. У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 2
3. Умножить на 2
Программа для исполнителя R17 – это последовательность команд. Сколько существует таких программ, которые исходное число 1 преобразуют в число 12 и при этом траектория вычислений программы содержит число 7 и число 10?
4.2) Исполнитель R17 преобразует число, записанное на экране. У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 2
3. Умножить на 3
Программа для исполнителя R17 – это последовательность команд. Сколько существует таких программ, которые исходное число 2 преобразуют в число 15 и при этом траектория вычислений программы содержит число 4 и число 11?

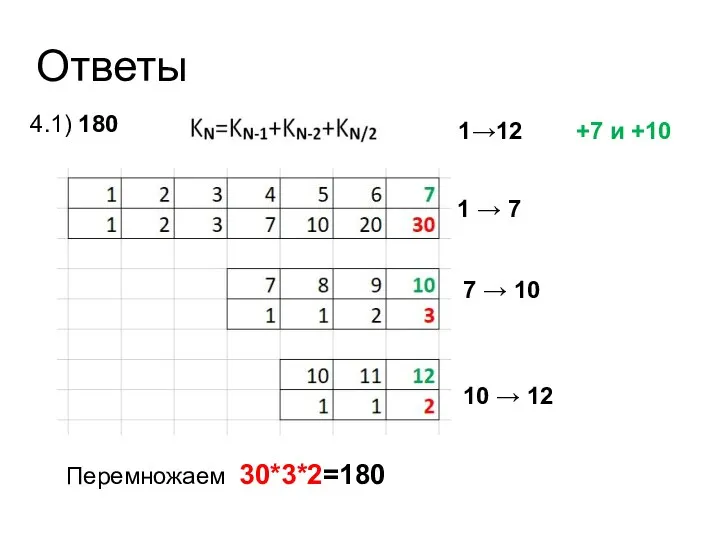
Ответы
4.1) 180
1→12 +7 и +10
Перемножаем 30*3*2=180
1 → 7
7 → 10
10 → 12

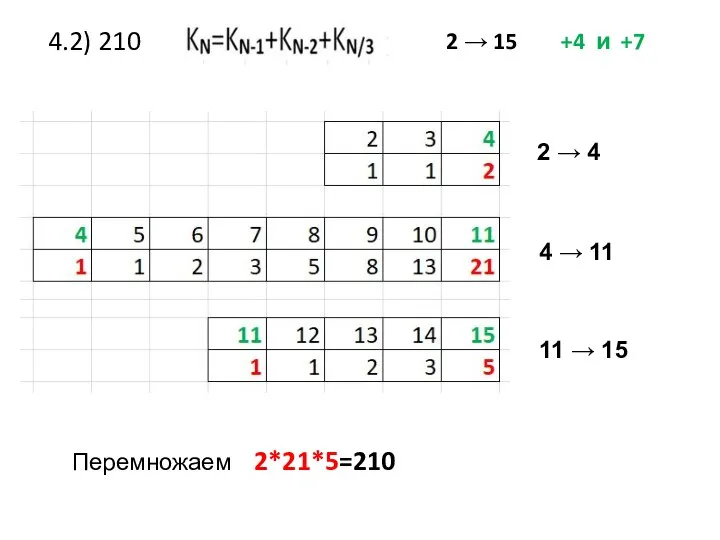
4.2) 210
2 → 15 +4 и +7
Перемножаем 2*21*5=210
2 → 4
4 → 11
11 → 15

Самостоятельно
5.1) Исполнитель Май18 преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 3
Сколько существует программ, для которых при исходном числе 2 результатом является число 18 и при этом траектория вычислений содержит число 9 и не содержит число 14?
5.2) Исполнитель Калькулятор преобразует число на экране. У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
3. Умножить на 3
Сколько существует программ, для которых при исходном числе 5 результатом является число 52 и при этом траектория вычислений содержит число 15 и не содержит число 29?

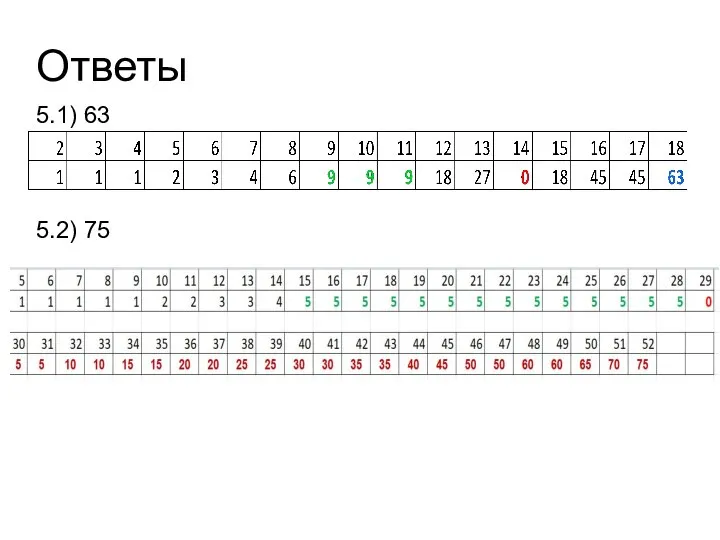
Ответы
5.1) 63
5.2) 75

Задача 4

Задача 4
У исполнителя Калькулятор две команды, которым присвоены номера:
1. прибавь 1
2. прибавь 3
Сколько есть программ, которые число 7 преобразуют в число 20 и при этом последняя команда 1?

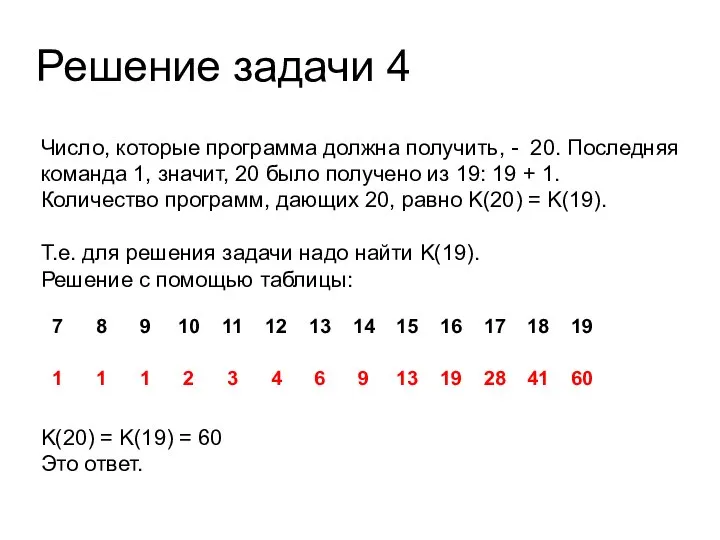
Решение задачи 4
Число, которые программа должна получить, - 20. Последняя команда 1, значит, 20 было получено из 19: 19 + 1.
Количество программ, дающих 20, равно K(20) = K(19).
Т.е. для решения задачи надо найти K(19).
Решение с помощью таблицы:
K(20) = K(19) = 60
Это ответ.

Самостоятельно

Самостоятельно
4.1) У исполнителя Калькулятор две команды, которым присвоены номера:
1. прибавь 1
2. прибавь 3
Сколько есть программ, которые число 1 преобразуют в число 15 и в которых последняя команда 2?

Ответы
4.1) 41

Задача 5

Задача 5
Исполнитель Калькулятор преобразует целое число, записанное на экране. У исполнителя две команды, каждой команде присвоен номер:
1. Прибавь 1
2. Умножь на 2
Первая команда увеличивает число на экране на 1, вторая увеличивает это число в 2 раза. Сколько существует программ, которые число 3 преобразуют в число 20 и в которых предпоследняя команда 1?

В условии сказано, что предпоследняя команда 1.
Последняя команда может быть любой – либо 1, либо 2.
Это означает, что нужно рассмотреть и получить количество всех команд вида «*11» и «*12».
Звездочка означает любую последовательность команд.
Решение задачи 5

Решение задачи 5
Если две последние команды «11», то
к числу 20 можно прийти :
от числа Х ⇒ (Х+1)+1=20; ⇒ Х = 18
Это значит, что нам нужно получить количество программ, преобразующих 3 в 18.

Если две последние команды «12»,
то к числу 20 можно прийти :
от числа У ⇒ (У+1)*2=20; ⇒ У= 9
Это значит, что нам нужно получить количество программ, преобразующих 3 в 9.
И сложить эти два результата.
Решение задачи 5

Число N могло быть получено одной из двух операций:
увеличением на 1 числа N-1;
умножением на 2 числа N/2 (только для четных N)
Общая рекуррентная формула: KN = KN-1 + KN/2
Если N нечетное, то считаем, что KN/2 = 0.

K9 = К8= 3
K8 = K7 + K4 =3
K7 = K6=2
K6 = K5+ K3=2
K5= K4=1
K4= K3 + K2 =1
К3=1
Количество программ 3→ 9 равно 3

3 → 9 = 3
3 → 18 =14
Всего : 3 + 14=17 программ
Ответ: 17
Количество программ 3→ 18 равно 14

Самостоятельно

Самостоятельно
5.1) Исполнитель Калькулятор преобразует целое число, записанное на экране. У исполнителя две команды, каждой команде присвоен номер:
1. Прибавь 1
2. Умножь на 2
Первая команда увеличивает число на экране на 1, вторая увеличивает это число в 2 раза. Сколько существует программ, которые число 5 преобразуют в число 32 и в которых предпоследняя команда 1?
5.2) Исполнитель Калькулятор преобразует целое число, записанное на экране. У исполнителя две команды, каждой команде присвоен номер:
1. Прибавь 1
2. Прибавь 2
Первая команда увеличивает число на экране на 1, вторая увеличивает – на 2. Сколько существует программ, которые число 3 преобразуют в число 18 и в которых предпоследняя команда 2?