Помехоустойчивое кодирование

Каждый может ошибиться, а если о чем-нибудь очень долго размышлять, уж наверняка ошибёшься.
Ярослав Гашек
Похождения бравого солдата Швейка

Необходимость помехоустойчивого кодирования:
Если в канале есть помехи, то при приеме кодовых символов могут произойти ошибки, тогда кодовые комбинации (полученные при эффективном кодировании) будут декодированы неправильно!
Задача: повышение верности передачи
Один из путей ее решения – помехоустойчивое (канальное) кодирование.

Такая возможность обеспечивается целенаправленным введением избыточности в передаваемые сообщения.
Помехоустойчивыми (корректирующими) кодами называются коды, обеспечивающие автоматическое обнаружение и/или исправление ошибок в кодовых комбинациях.

При кодировании источника избыточность уменьшается или полностью устраняется (достигается увеличение скорости передачи информации за счёт уменьшения средней длины кодовых слов)
Наиболее простой способ:
например, вместо слова стол можно передавать слово ссстттоооллл
При помехоустойчивом кодировании в передаваемые сообщения вводится избыточность (количество символов увнличивается!)
За счет этого появляется возможность обнаруживать ошибки и даже исправлять их

2-я Теорема Шеннона (Основная теорема кодирования для каналов с помехами (шумами)
Если производительность источника меньше пропускной способности канала то существует по крайней мере одна процедура кодирования/декодирования, при которой вероятность ошибочного декодирования и ненадежность могут быть сколь угодно малы. Если то такой процедуры не существует.
В вышеприведённом примере ясно, что при фиксированном уровне помех для стремления вероятности ошибки к нулю количество повторений должно стремиться к бесконечности.
Скорость передачи информации при этом стремится к нулю.

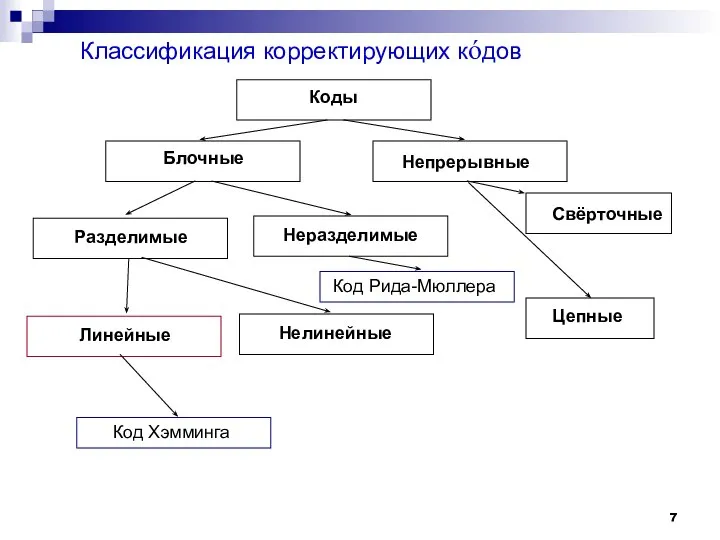
Классификация корректирующих кóдов
Коды
Блочные
Непрерывные
Разделимые
Неразделимые
Свёрточные
Линейные
Нелинейные
Код Рида-Мюллера
Код Хэмминга
Цепные

Линейные блочные кóды
Блочный равномерный код – множество кодовых слов (комбинаций) одинаковой длины n.
Элементы кодовых слов выбираются из некоторого алфавита (канальных) символов объемом q.
Если q =2, код называется двоичным. Далее для простоты считается, что q =2.

Линейные блочные кóды
Поскольку все кодовые слова имеют одинаковую длину, удобно считать их векторами, принадлежащими линейному пространству размерности n.
Для линейных кóдов справедливо утверждение: линейная комбинация кодовых слов является кодовым словом.
00110100101101
…………………..
01001110100100

Из них только комбинаций являются разрешёнными и составляют код, который называется -кодом (отношение называется относительной скоростью кода).
Всего n-мерных векторов с двоичными компонентами (кодовых комбинаций или слов).
Остальные комбинации являются запрещёнными, образуются из разрешённых в канале под воздействием помех.

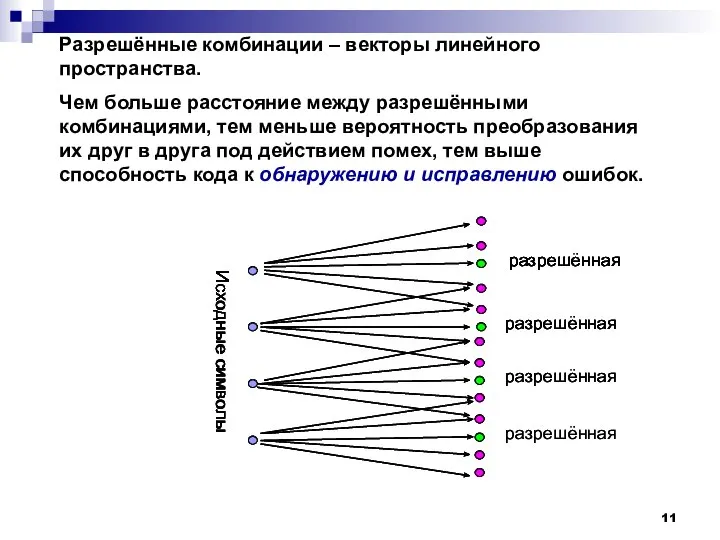
Разрешённые комбинации – векторы линейного пространства.
Чем больше расстояние между разрешёнными комбинациями, тем меньше вероятность преобразования их друг в друга под действием помех, тем выше способность кода к обнаружению и исправлению ошибок.
Исходные символы
разрешенная
разрешенная
разрешенная
разрешенная
Исходные символы
разрешенная
разрешенная
Исходные символы
разрешенная
разрешенная
разрешенная
Исходные символы
разрешенная
разрешённая
разрешённая
разрешённая
Исходные символы
разрешённая

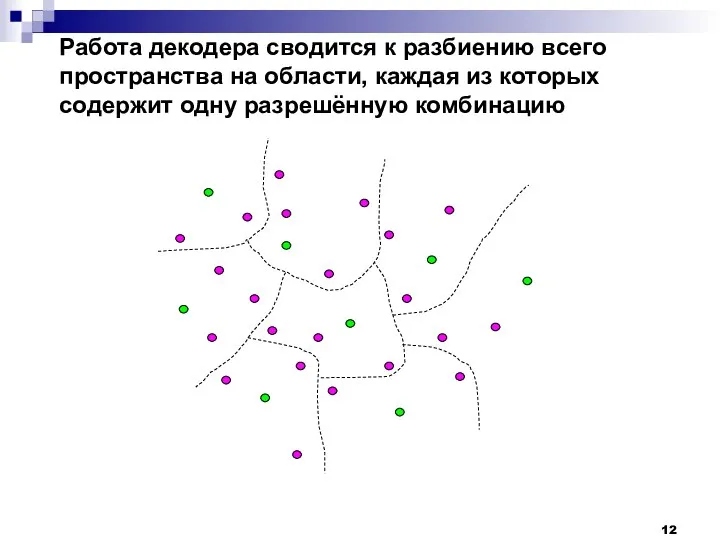
Работа декодера сводится к разбиению всего пространства на области, каждая из которых содержит одну разрешённую комбинацию

Для кодирования и декодирования линейных блочных кодов применяются действия, описываемые операциями над векторами в линейном пространстве над конечным полем целых чисел
Сложение и умножение в конечном поле понимаются как сложение и умножение по модулю q
Простейшее из таких полей, называемых полями Галуá – поле по модулю 2, обозначаемое GF(2)
ЭВАРИСТ ГАЛУА
Évariste Galois
(1811-1832)
выдающийся французский математик, основатель современной алгебры.

Заметим, что вычитание по модулю 2 совпадает со сложением по модулю 2

Метрика (расстояние) Хэмминга, определяемая для двух двоичных кодовых векторов выражением
Расстояние по Хэммингу между двумя двоичными векторами равно количеству несовпадающих элементов
Скалярное произведение можно определить выражением
Итак, множество всех двоичных кодовых слов длины n можно рассматривать, как n-мерное линейное пространство над конечным полем скаляров GF(2).

Линейные коды являются разделимыми, то есть k символов – информационные, остальные (n-k) − проверочные.
Информационные символы зависят от передаваемого сообщения и могут быть какими угодно.
Проверочные символы однозначно определяются информационными (т.к. формируются из информационных символов кодером, работающим по определённому алгоритму).
Отсюда следует, что каждая кодовая комбинация, будучи вектором n-мерного пространства, принадлежит его k-мерному подпространству

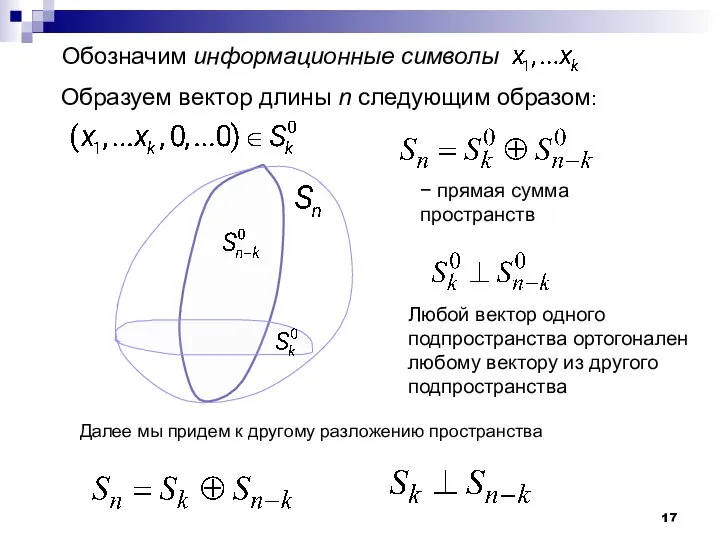
Обозначим информационные символы
Образуем вектор длины n следующим образом:
− прямая сумма пространств
Любой вектор одного подпространства ортогонален любому вектору из другого подпространства
Далее мы придем к другому разложению пространства

Обозначим информационный вектор
а кодовый вектор
Кодирование описывается линейным преобразованием (оператором), отображающим векторы, соответствующие подпространству , в векторы из :
Матрица кодирования

Подробнее:
Или

Любой кодовый вектор (кодовое слово) является линейной комбинацией строк матрицы, а поскольку строк ровно k, то
все разрешенные кодовые слова принадлежат k-мерному подпространству, натянутому на строки матрицы, как на базис.
Таким образом, при кодировании информационного вектора подпространство преобразуется линейным образом, но остается k-мерным подпространством
Очевидно, что кодовая матрица должна состоять из линейно независимых строк (иначе размерности подпространства не хватит для представления k-мерного информационного вектора).

Путём линейных операций над строками и перестановки столбцов любую такую матрицу можно привести к систематическому виду
k первых символов повторяют символы информационного вектора, а остальные (n-k) символов формируются из информационных и являются проверочными (паритетными).
В этом случае код называют систематическим.

Пример. Систематический код (7,4) порождается матрицей
Кодовые слова имеют структуру
где

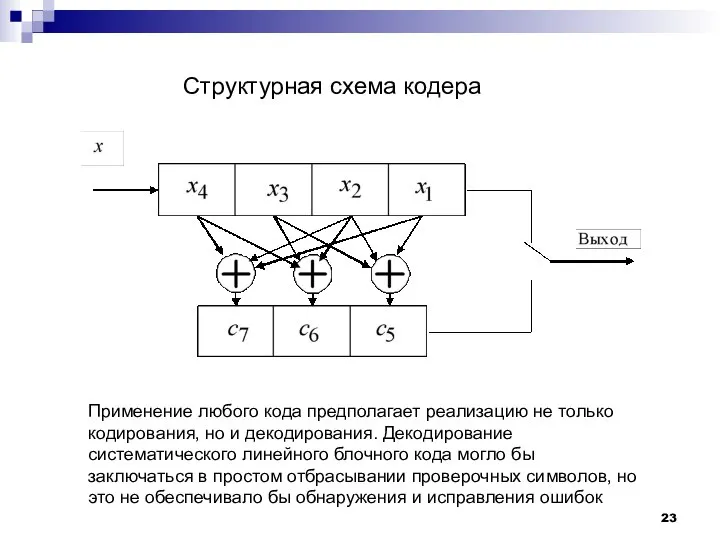
Структурная схема кодера
Применение любого кода предполагает реализацию не только кодирования, но и декодирования. Декодирование систематического линейного блочного кода могло бы заключаться в простом отбрасывании проверочных символов, но это не обеспечивало бы обнаружения и исправления ошибок

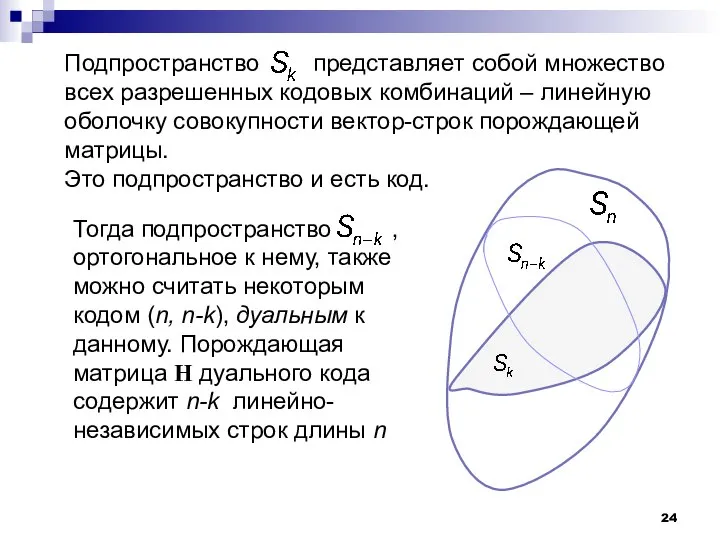
Подпространство представляет собой множество всех разрешенных кодовых комбинаций – линейную оболочку совокупности вектор-строк порождающей матрицы.
Это подпространство и есть код.
Тогда подпространство , ортогональное к нему, также можно считать некоторым кодом (n, n-k), дуальным к данному. Порождающая матрица H дуального кода содержит n-k линейно-независимых строк длины n

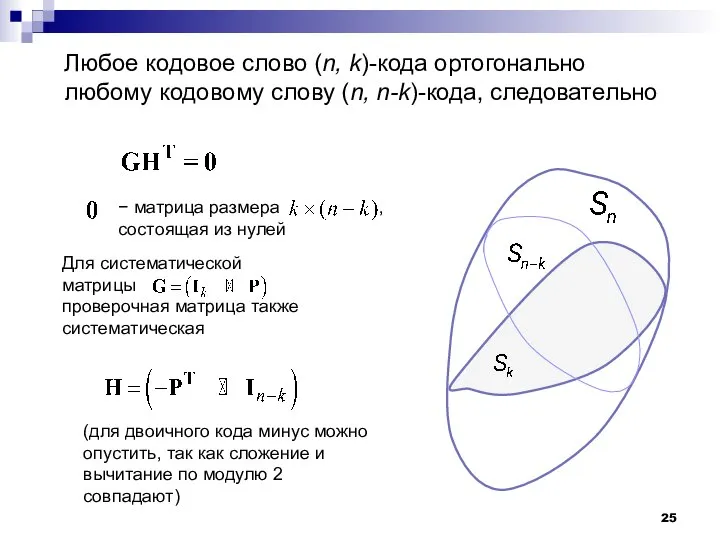
Любое кодовое слово (n, k)-кода ортогонально любому кодовому слову (n, n-k)-кода, следовательно
− матрица размера , состоящая из нулей
Для систематической матрицы
проверочная матрица также систематическая
(для двоичного кода минус можно опустить, так как сложение и вычитание по модулю 2 совпадают)

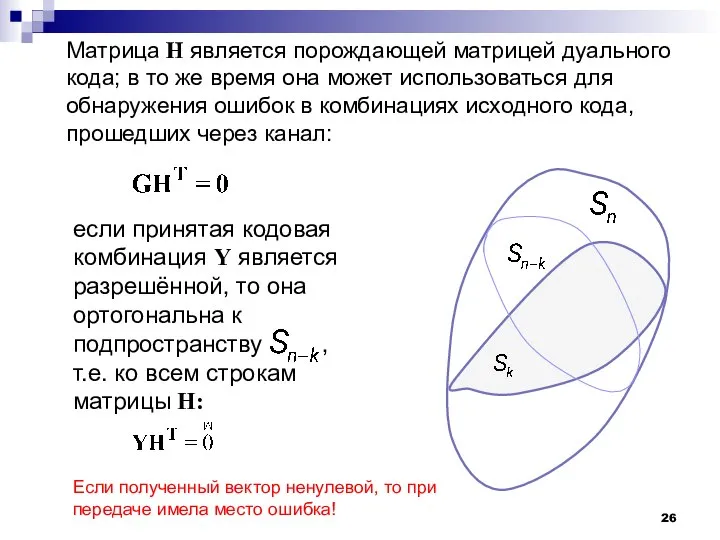
Матрица Н является порождающей матрицей дуального кода; в то же время она может использоваться для обнаружения ошибок в комбинациях исходного кода, прошедших через канал:
если принятая кодовая комбинация Y является разрешённой, то она ортогональна к подпространству ,
т.е. ко всем строкам матрицы Н:
Если полученный вектор ненулевой, то при передаче имела место ошибка!

Умножая слева вектор-строку, соответствующую принятой комбинации, на транспонированную матрицу , получаем вектор (называемый синдромом), который равен нулевому вектору в том и только в том случае, если комбинация является разрешённой. В противном случае комбинация является запрещённой, следовательно, при передаче произошла ошибка. По значению синдрома можно определить, какой именно разряд кодового слова содержит ошибку (а при двоичном коде – и исправить её!).

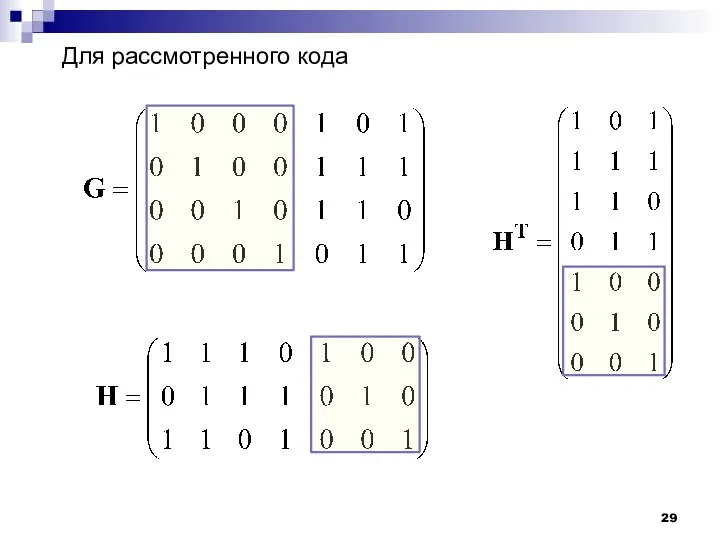
Коды Хэмминга
Коды Хэмминга представляют собой (n, k)-коды, удовлетворяющие условию
В частности, рассмотренный (7,4)-код принадлежит к кодам Хэмминга при m=3
Для кода Хэмминга проверочная матрица содержит в качестве столбцов все возможные -значные комбинации нулей и единиц, исключая нулевой вектор.

Для рассмотренного кода

Пример. Предположим, что передавалась разрешённая комбинация 0100111, а при передаче произошла ошибка, скажем, во втором символе, так что принятá комбинация 0000111.
Умножая вектор-строку (принятую комбинацию), слева на , получим синдром
Полученный синдром указывает на второй символ принятой комбинации, как ошибочный. Для исправления достаточно прибавить к кодовой комбинации комбинацию 0100000

Пример. Предположим, что при передаче разрешенной кодовой комбинации 0100111 произошли две ошибки, скажем, в третьем и пятом символах, так что принята комбинация 0110011. Найдем синдром:
Полученный синдром совпадает с шестой строкой матрицы, что указывает на шестой символ принятой комбинации, как ошибочный. Прибавление комбинации 0000010 к принятой кодовой комбинации, очевидно, не исправляет её.

Итак, код Хэмминга (7,4) обнаруживает одно- и двукратные ошибки и исправляет однократные.
Расстояние между любыми двумя разрешенными комбинациями этого кода не менее 3. Поэтому при приёме запрещенной комбинации она заменяется той разрешенной комбинацией, расстояние до которой равно 1. Двукратная ошибка отдаляет принимаемую комбинацию на расстояние, равное 2, что и приводит к ошибочному «исправлению» ошибки. При этом «исправляется» один символ, поэтому «исправленная» комбинация отстоит от принятой на расстояние 1.
Исходные символы
разрешенная
разрешенная
разрешенная
разрешенная

Коды, обнаруживающие ошибки, но не исправляющие их, могут использоваться в системах с решающей обратной связью (системах с переспросом). В таких системах при обнаружении ошибки во время декодирования по каналу обратной связи передается сигнал переспроса, и тогда передающее устройство повторяет передачу забракованной комбинации.

При решении вопроса о целесообразности помехоустойчивого кодирования и выборе помехоустойчивого кода следует руководствоваться критерием максимума скорости передачи информации при заданной верности.
Введение избыточных символов приводит к:
увеличению времени передачи кодовой комбинации (при постоянной ширине спектра)
укорочению элементарных посылок и расширению спектра(при неизменном времени)
при укорочении посылок приходится увеличивать мощность передатчика, иначе – увеличение вероятности ошибочного приема символа.