Построение функциональных схем по логическим функциям

Самостоятельная работа
Тема: «Построение функциональных схем по логическим функциям»

Построение функциональных схем по логическим функциям
Ставится задача освоить алгоритм построения функциональных схем логических устройств по известной логической функции.
Для сравнения получаемых результатов рассмотрим построение функциональной схемы одного и того же устройства, выбирая разный элементный базис. Фраза «одно и то же устройство» означает, что в основе построения лежит одна и та же логическая функция.
Пусть работа некоторого устройства описывается логической функцией:
В данном случае не ставится условие минимизировать эту функцию, так как решается иная задача!

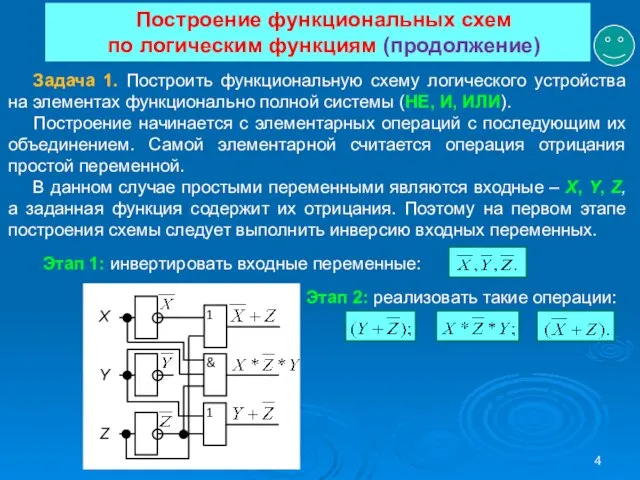
Построение функциональных схем
по логическим функциям (продолжение)
Задача 1. Построить функциональную схему логического устройства на элементах функционально полной системы (НЕ, И, ИЛИ).
Построение начинается с элементарных операций с последующим их объединением. Самой элементарной считается операция отрицания простой переменной.
В данном случае простыми переменными являются входные – X, Y, Z, а заданная функция содержит их отрицания. Поэтому на первом этапе построения схемы следует выполнить инверсию входных переменных.
Этап 1: инвертировать входные переменные:
Z
X
Y
Этап 2: реализовать такие операции:

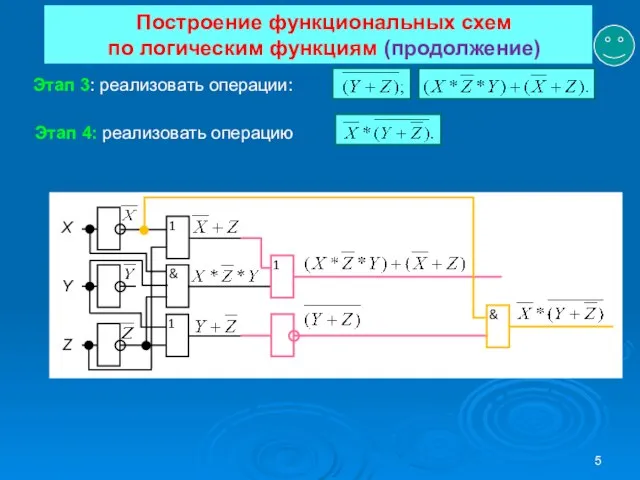
Построение функциональных схем
по логическим функциям (продолжение)
Этап 3: реализовать операции:
Этап 4: реализовать операцию

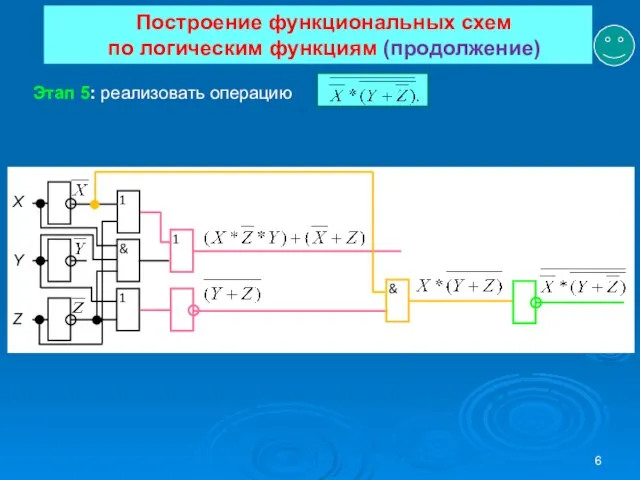
Построение функциональных схем
по логическим функциям (продолжение)
Этап 5: реализовать операцию

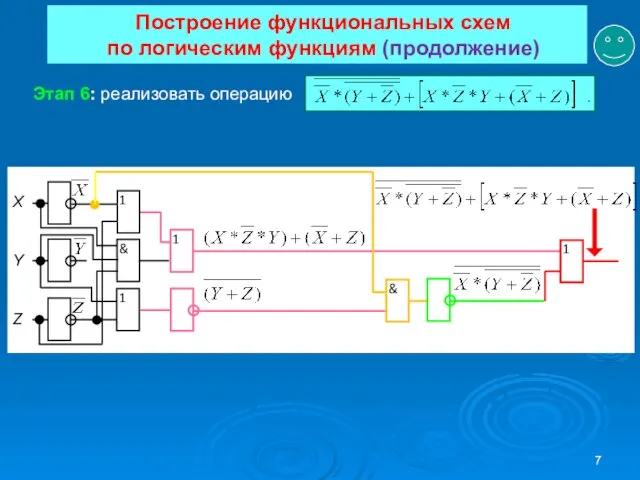
Построение функциональных схем
по логическим функциям (продолжение)
Этап 6: реализовать операцию

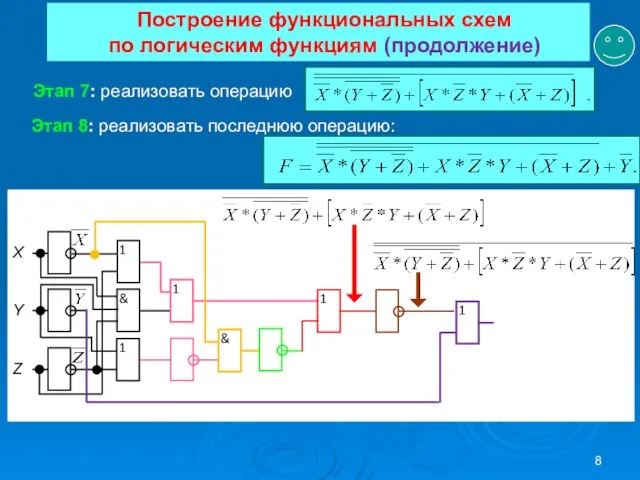
Построение функциональных схем
по логическим функциям (продолжение)
Этап 7: реализовать операцию
Этап 8: реализовать последнюю операцию:
F

Построение функциональных схем
по логическим функциям (продолжение)
Заключение.
Функциональная схема построена за 8 этапов.
В составе схемы 13 логических элементов.
(Запомним эти данные для сравнительной оценки с последующими результатами).

Задача 2. Построить функциональную схему логического устройства с использованием элементов базиса И-НЕ.
Работа устройства описывается той же логической функцией, что и в примере 1:
Элементы И-НЕ не могут выполнять логическую операцию ИЛИ. Поэтому предварительно нужно выполнить преобразование логической функции, исключив операции ИЛИ.
Построение функциональных схем
по логическим функциям (продолжение)

Этап 1. Преобразование базируется на теореме де Моргана. При отсутствии навыков проще всего выполнить преобразование последовательно «от частного к общему».
Выделим два набора:
Построение функциональных схем
по логическим функциям (продолжение)
Применим к этим наборам теорему.
В результате этих преобразований логическая функция примет вид:
Введём обозначения:
Тогда:

Построение функциональных схем
по логическим функциям (продолжение)
К набору
применим теорему де Моргана и получим
Устраним последнее логическое сложение:
И в итоге «рабочая» логическая функция примет вид:
Логическая функция примет вид:

Построение функциональных схем
по логическим функциям (продолжение)
Этап 2. Нужен элемент, выполняющий только операцию НЕ. Он может быть получен из элемента И-НЕ в результате объединения всех входов.
Действительно, элемент НЕ имеет только один вход. У элемента И-НЕ как минимум два входа. Из таблицы истинности элемента И-НЕ
следует, что при подаче на все входы одноуровневых сигналов уровень сигнала на выходе элемента инвертируется.
Тогда элемент НЕ примет вид:

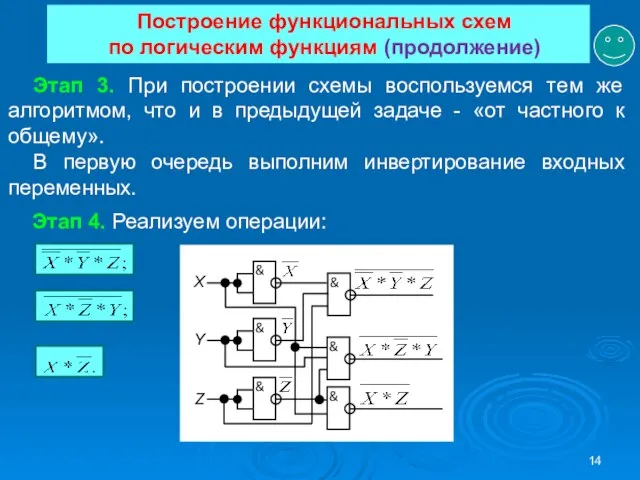
Построение функциональных схем
по логическим функциям (продолжение)
Этап 3. При построении схемы воспользуемся тем же алгоритмом, что и в предыдущей задаче - «от частного к общему».
В первую очередь выполним инвертирование входных переменных.
Z
X
Y
Этап 4. Реализуем операции:

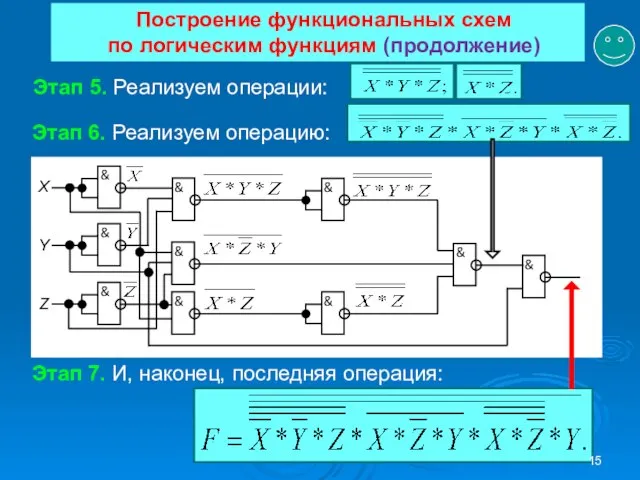
Построение функциональных схем
по логическим функциям (продолжение)
Этап 5. Реализуем операции:
Этап 6. Реализуем операцию:
Этап 7. И, наконец, последняя операция:

Построение функциональных схем
по логическим функциям (продолжение)
Заключение.
Функциональная схема построена за 6 этапов.
В составе схемы 10 логических элементов.

Построение функциональных схем
по логическим функциям (продолжение)
Задача 3. Построить функциональную схему логического устройства с использованием элементов базиса ИЛИ-НЕ.
Работа устройства описывается той же логической функцией, что и в примере 1:
Элементы ИЛИ-НЕ не могут выполнять логическую операцию И. Поэтому предварительно нужно выполнить преобразование логической функции, исключив операции И.

Этап 1. Преобразование базируется на теореме де Моргана.
Выделим два набора:
Построение функциональных схем по логическим функциям (продолжение)
Применим к этим наборам теорему.
В результате этих преобразований логическая функция примет вид:

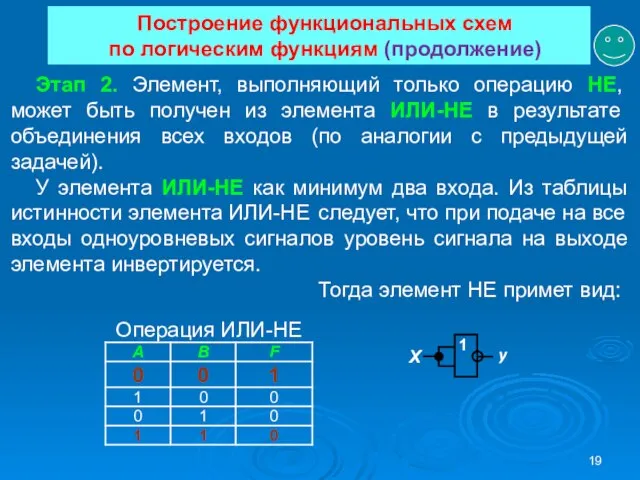
Построение функциональных схем
по логическим функциям (продолжение)
Этап 2. Элемент, выполняющий только операцию НЕ, может быть получен из элемента ИЛИ-НЕ в результате объединения всех входов (по аналогии с предыдущей задачей).
У элемента ИЛИ-НЕ как минимум два входа. Из таблицы истинности элемента ИЛИ-НЕ
следует, что при подаче на все входы одноуровневых сигналов уровень сигнала на выходе элемента инвертируется.
Тогда элемент НЕ примет вид:

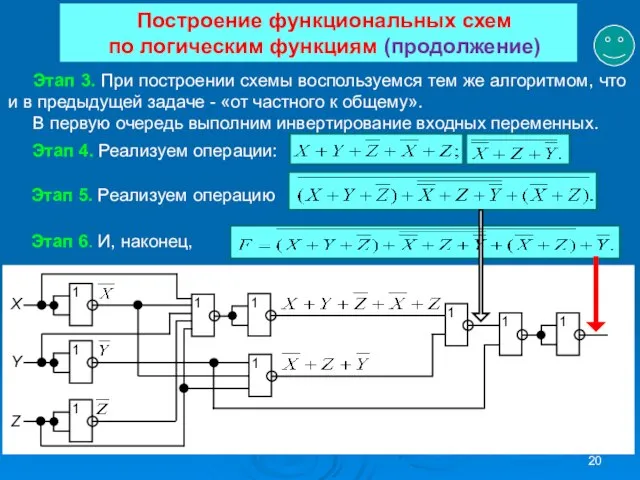
Построение функциональных схем
по логическим функциям (продолжение)
Этап 3. При построении схемы воспользуемся тем же алгоритмом, что и в предыдущей задаче - «от частного к общему».
В первую очередь выполним инвертирование входных переменных.
X
Z
Y
Этап 4. Реализуем операции:
Этап 5. Реализуем операцию
Этап 6. И, наконец,

Построение функциональных схем
по логическим функциям (продолжение)
Заключение.
Функциональная схема построена за 5 этапов.
В составе схемы 9 логических элементов.

Построение функциональных схем
по логическим функциям (продолжение)
Задача 4. Построить функциональную схему логического устройства с использованием элементов базиса И-НЕ.
Работа устройства описывается той же логической функцией, что и в примерах 1, 2 и 3, но предварительно требуется её минимизировать:
Видно, что для реализации такой функции необходим всего один элемент.