Представление чисел в памяти компьютера (10 класс)

Образ компьютерной памяти

Главные правила представления данных в компьютере

Правило 1
Данные (и программы) в памяти компьютера хранятся в двоичном виде,
т. е. в виде цепочек единиц и нулей.

Правило 2
Представление данных в компьютере дискретно.
Дискретное множество состоит из отделенных друг от друга элементов.

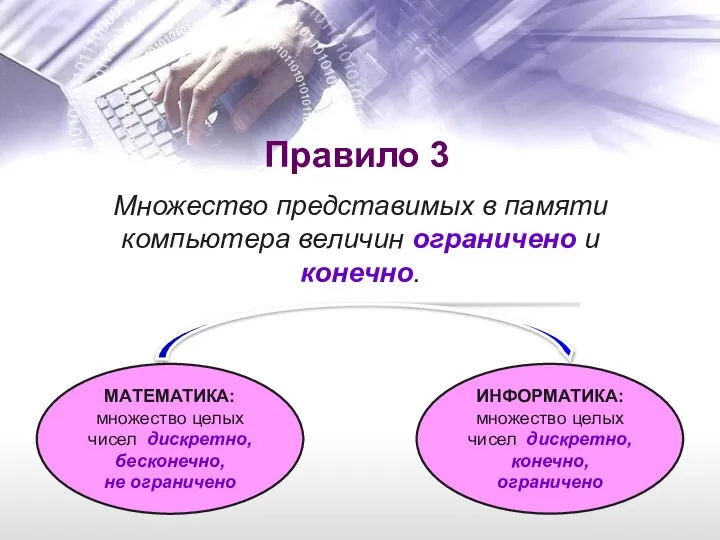
Правило 3
Множество представимых в памяти компьютера величин ограничено и конечно.
МАТЕМАТИКА:
множество целых чисел дискретно, бесконечно,
не ограничено
ИНФОРМАТИКА:
множество целых чисел дискретно, конечно, ограничено

Правило 4
В памяти компьютера числа хранятся в двоичной системе счисления.

Для представления чисел в памяти компьютера используются два формата: формат с фиксированной точкой и формат с плавающей точкой.
В формате с фиксированной точкой представляются только целые числа,
в формате с плавающей точкой – вещественные числа (целые и дробные).
Целые числа могут представляться в компьютере со знаком или без знака.

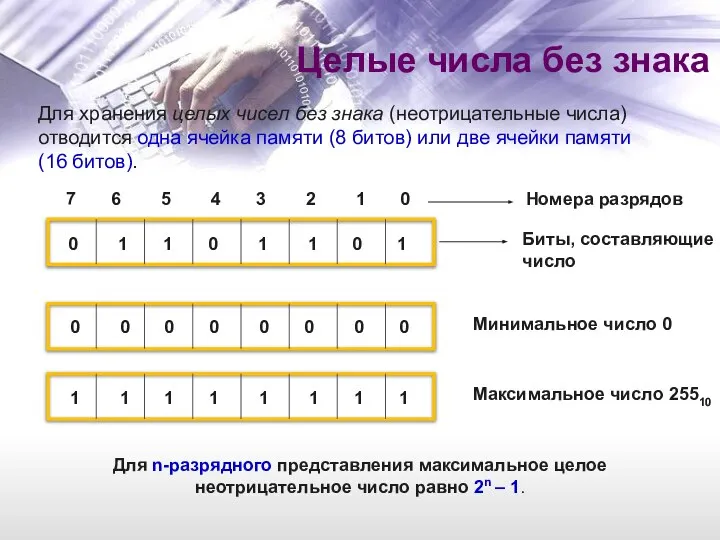
Для хранения целых чисел без знака (неотрицательные числа) отводится одна ячейка памяти (8 битов) или две ячейки памяти (16 битов).
7 6 5 4 3 2 1 0
Номера разрядов
Биты, составляющие
число
Минимальное число 0
Максимальное число 25510
Для n-разрядного представления максимальное целое неотрицательное число равно 2n – 1.
Целые числа без знака

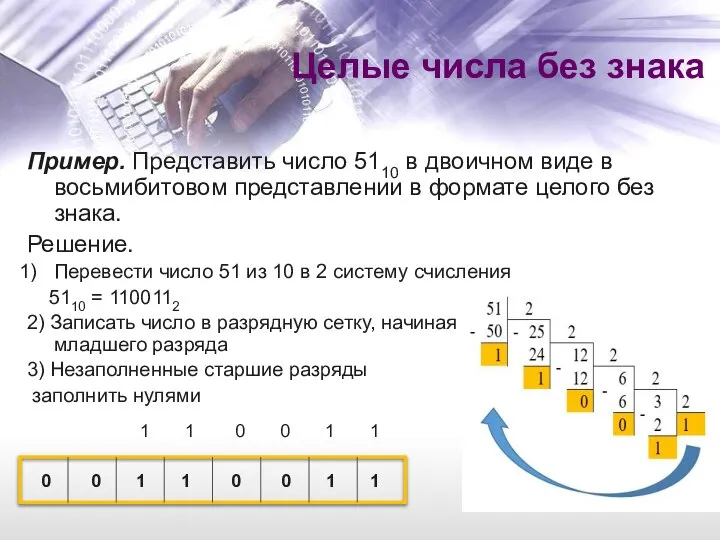
Пример. Представить число 5110 в двоичном виде в восьмибитовом представлении в формате целого без знака.
Решение.
Перевести число 51 из 10 в 2 систему счисления
5110 = 1100112
2) Записать число в разрядную сетку, начиная с
младшего разряда
3) Незаполненные старшие разряды
заполнить нулями
Целые числа без знака
1 1 0 0 1 1

Для хранения целых чисел со знаком отводится
одна, две или четыре ячейки памяти (8, 16, 32 битов соответственно).
Старший разряд числа определяет его знак.
Если он равен 0, число положительное, если 1, то отрицательное.
5110 = 1100112
- 5110 = - 1100112
Целые числа со знаком
Знак числа
Алгоритм
1) Перевести модуль числа в 2 систему счисления
2) Записать число в разрядную сетку, начиная с младшего разряда
3) В старший разряд записать знак числа ( 0 или 1)
4) Пустые разряды заполнить 0

Для n-разрядного представления целого числа со знаком (с учетом выделения одного разряда на знак):
минимальное отрицательное число равно – 2n-1
максимальное положительное число равно 2n-1 – 1,
Целые числа в памяти компьютера —
это дискретное, ограниченное и конечное множество.
Целые числа со знаком

Упражнение 1
Определить максимальное положительное число, которое может храниться в оперативной памяти в формате целое число со знаком в двухбайтном представлении.
Решение
А=2n-1 – 1
А10=215 – 1 = 3276710

В ЭВМ в целях упрощения выполнения арифметических операций применяют
специальные коды для представления целых чисел
Прямой код числа
Обратный код числа
Дополнительный код числа

Прямой код – это представление числа в двоичной системе счисления, при этом первый разряд отводится под знак числа. Если число положительное, то в первом разряде находится 0, если число отрицательное, в первом разряде указывается 1.

5110 = 1100112
- 5110 = - 1100112
Обратный код для положительного числа в двоичной системе счисления совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Прямой код
Обратный код
Прямой код
Обратный код

Дополнительный код используют в основном для представления в компьютере отрицательных чисел.
Алгоритм получения дополнительного кода для отрицательного числа
1. Найти прямой код числа ( перевести число в двоичную систему счисления число без знака)
2. Получить обратный код. Поменять каждый ноль на единицу, а единицу на ноль ( инвертировать число). В знаковом разряде 1.
3. К обратному коду прибавить 1

Найти дополнительный код десятичного числа – 47 ( в 16-битном коде)
Перевести модуль числа -47 в двоичную систему счисления
4710=1011112( прямой код)
2. Записать число в разрядную сетку, начиная с младшего разряда
3. Т.к. число отрицательное в старший разряд записать знак числа.
4. Пустые разряды заполнить 0
2. Инвертируем это число. В знаковом разряде 1. ( обратный код)
3. Прибавим к младшему разряду обратного кода 1 и получим запись этого числа в оперативной памяти
Прямой код
+1
Упражнение 2

Вещественные числа
Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей запятой, использующем экспоненциальную форму записи чисел.
A = M ? qn
M – мантисса числа (правильная отличная от нуля дробь),
q – основание системы счисления,
n – порядок числа.
Диапазон ограничен максимальными значениями M и n.

Вещественные числа
Например, 123,45 = 0,12345 · 103
Порядок указывает, на какое количество позиций и в каком направлении должна сместиться десятичная запятая в мантиссе.
Число в формате с плавающей запятой может занимать в памяти 4 байта (обычная точность) или 8 байтов (двойная точность).
При записи числа выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.
Мантисса M и порядок n определяют диапазон изменения чисел и их точность.

Домашнее задание
§ 5

Практическая работа №3 «Представлене чисел»
Задание 1.
Записать внутреннее представление следующих десятичных чисел со знаком, используя 8 – разрядную ячейку:
6410
- 12010