Содержание
- 2. Статистическая обработка данных. Ребята, мы переходим к изучению нового раздела, связанного с вопросами обработки данных различных
- 3. Статистическая обработка данных. Давайте рассмотрим какой-нибудь пример, где нам может пригодиться обработка информации. Пусть у нас
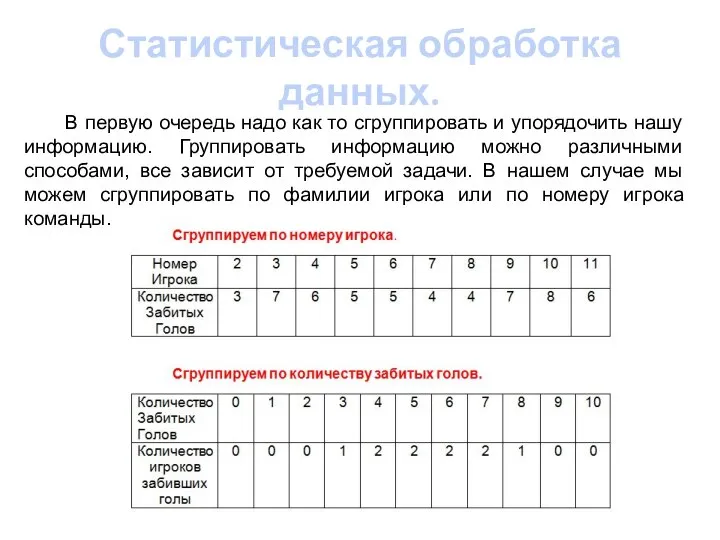
- 4. Статистическая обработка данных. В первую очередь надо как то сгруппировать и упорядочить нашу информацию. Группировать информацию
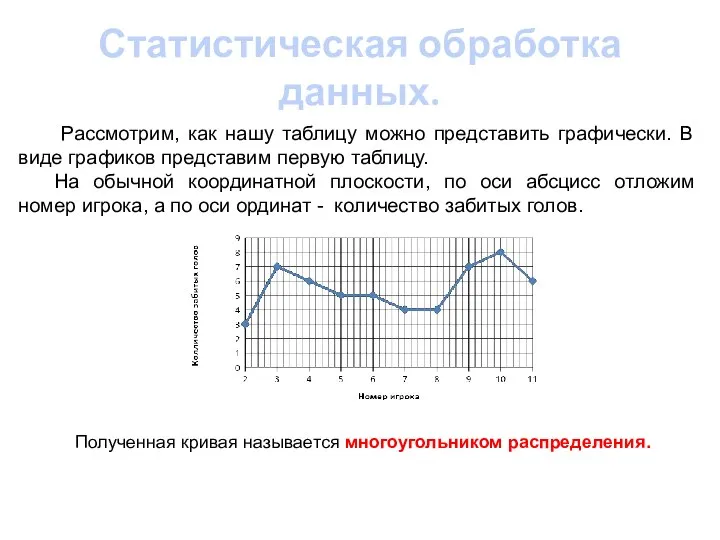
- 5. Статистическая обработка данных. Рассмотрим, как нашу таблицу можно представить графически. В виде графиков представим первую таблицу.
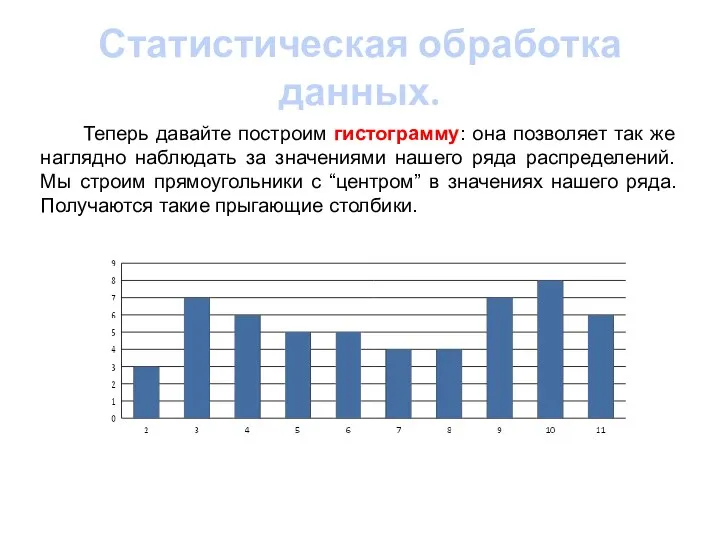
- 6. Статистическая обработка данных. Теперь давайте построим гистограмму: она позволяет так же наглядно наблюдать за значениями нашего
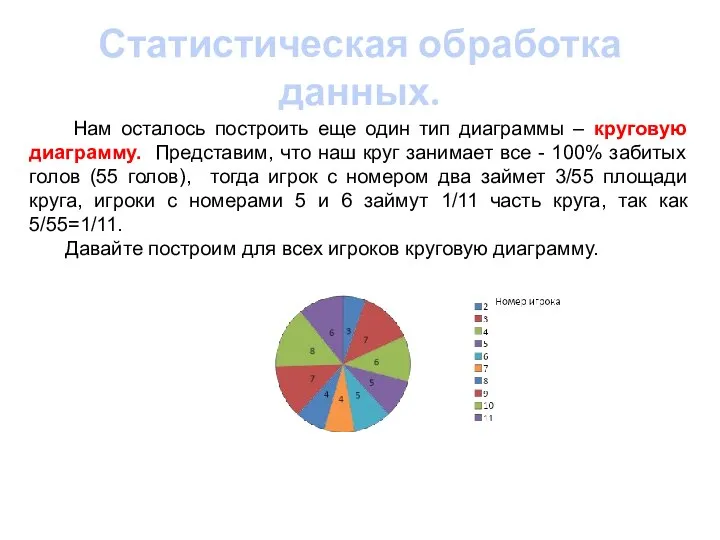
- 7. Статистическая обработка данных. Нам осталось построить еще один тип диаграммы – круговую диаграмму. Представим, что наш
- 8. Статистическая обработка данных. Ну вот, мы с вами научились немного обрабатывать данные. Давайте напишем небольшой алгоритм
- 9. Статистическая обработка данных. Но на этом обработка информации не заканчивается, для нашего ряда распределения можно найти
- 10. Статистическая обработка данных. Среднее значение выборки. Суммируя все результаты и поделив на оббьем выборки можно получить
- 11. Статистическая обработка данных. Варианта измерения – каждое число встретившиеся в результате измерения. В нашем случае для
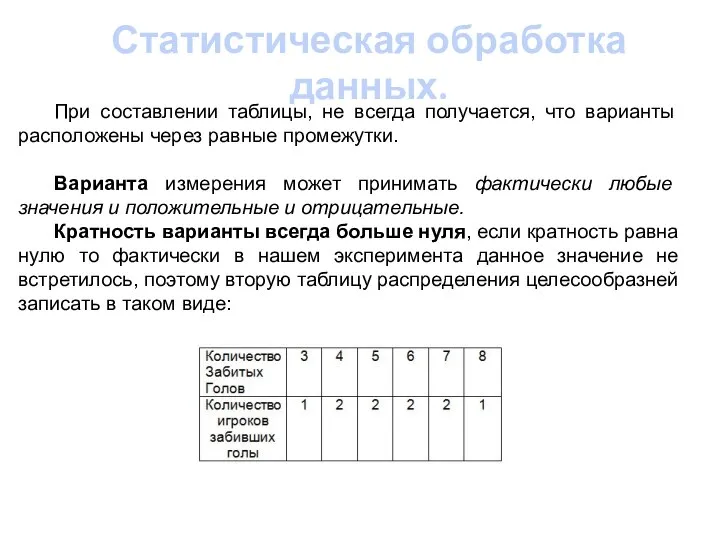
- 12. Статистическая обработка данных. При составлении таблицы, не всегда получается, что варианты расположены через равные промежутки. Варианта
- 13. Статистическая обработка данных. Варианта измерения – каждое число встретившиеся в результате измерения. В нашем случае для
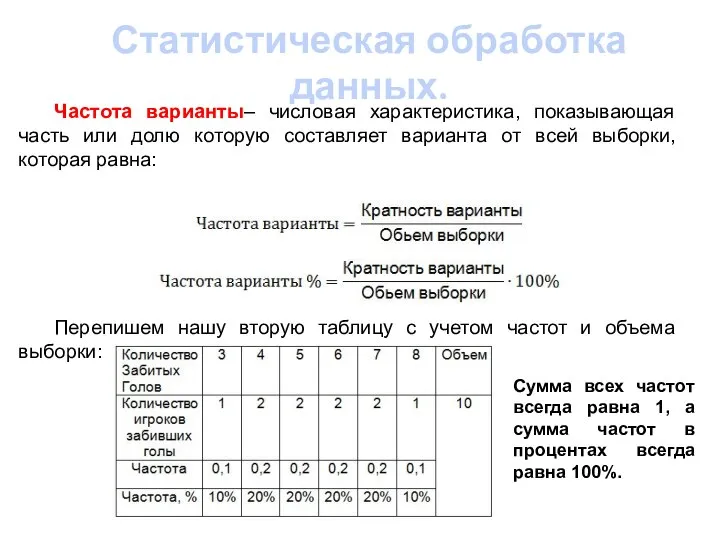
- 14. Статистическая обработка данных. Частота варианты– числовая характеристика, показывающая часть или долю которую составляет варианта от всей
- 15. Статистическая обработка данных. Вернемся к среднему значению, данная числовая характеристика часто является очень полезной. Но не
- 16. Статистическая обработка данных. Еще одна важная числовая характеристика – Дисперсия, или разброс значений вокруг среднего значения.
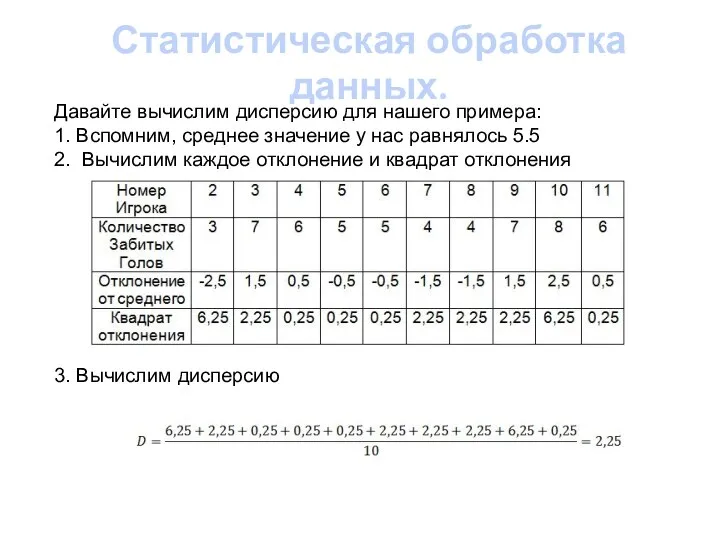
- 17. Статистическая обработка данных. Давайте вычислим дисперсию для нашего примера: 1. Вспомним, среднее значение у нас равнялось
- 18. Статистическая обработка данных. Методы математической статистики позволяют обрабатывать практически любые данные, главное подходить к обработке данных
- 20. Скачать презентацию










 Choose a random element from a non-empty sequence
Choose a random element from a non-empty sequence WinUI. The modern native Ul platform of Windows
WinUI. The modern native Ul platform of Windows Презентация на тему Возможности операционной системы Linux в учебном процессе Возможности операционной системы Linux в учебном процес
Презентация на тему Возможности операционной системы Linux в учебном процессе Возможности операционной системы Linux в учебном процес Создание игрового портала
Создание игрового портала Электронные таблицы. Обработка числовой информации в электронных таблицах
Электронные таблицы. Обработка числовой информации в электронных таблицах Эпиграфы
Эпиграфы Моделирование в среде графического редактора (урок информатики)
Моделирование в среде графического редактора (урок информатики) Текстовый процессор Writer
Текстовый процессор Writer Точные и приближенные методы
Точные и приближенные методы Летний интенсив Марс атакует! Порядок действий ликвидации последствий сбоев системы, кибератак
Летний интенсив Марс атакует! Порядок действий ликвидации последствий сбоев системы, кибератак TeamLead команды SMART
TeamLead команды SMART Co są sieci nieuronowe
Co są sieci nieuronowe Регистрация в системе Нмо
Регистрация в системе Нмо О применении алгоритма CLAHE к обработке спектрозональных изображений
О применении алгоритма CLAHE к обработке спектрозональных изображений Электронные таблицы. Обработка числовой информации в электронных таблицах
Электронные таблицы. Обработка числовой информации в электронных таблицах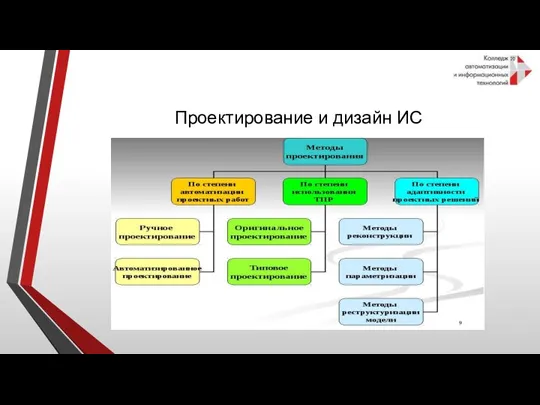 Проектирование и дизайн ИС
Проектирование и дизайн ИС Метод розпізнавання облич на основі AI сервісу Microsoft Azure та OpenCV
Метод розпізнавання облич на основі AI сервісу Microsoft Azure та OpenCV Киберспорт в жизни человека
Киберспорт в жизни человека Понятие растровой графики
Понятие растровой графики Отчет о деятельности Пресс-центра ППОС СФУ за 2018 год
Отчет о деятельности Пресс-центра ППОС СФУ за 2018 год Презентация на тему Персональный компьютер как система (7 класс)
Презентация на тему Персональный компьютер как система (7 класс)  Налог за российских блогеров с доходов от рекламы в блоге
Налог за российских блогеров с доходов от рекламы в блоге Интерфейс Scratch
Интерфейс Scratch 18_HTML5__
18_HTML5__ Представление и организация данных в ПК. Лекция 2-3
Представление и организация данных в ПК. Лекция 2-3 Создание и разрушение объектов
Создание и разрушение объектов Формулы и функции
Формулы и функции Эволюция компьютерного вируса
Эволюция компьютерного вируса