Презентация на тему Алгоритмы на графах: определение наличия циклов в графе

Домашнее задание
Какое максимальное количество рёбер может быть в ориентированном ациклическом графе с n вершинами?
Может ли быть так, что правильным результатом топологической сортировки графа оказывается любой порядок его вершин?
Решить задачу о производстве деталей с помощью DFS.
Как использовать топологическую сортировку для определения наличия циклов в графе?

Циклы и топологическая сортировка
Если в графе есть циклы, то топологическая сортировка невозможна.
Если граф ациклический, то можно выполнить топологическую сортировку.
Как с помощью топологической сортировки определить наличие циклов в графе?
Pascal
Cycles := False;
for i := 1 to n do
for j := 1 to n do
if A[i, j] and
(order[j] > order[i]) then
Cycles := True;
C
Cycles = FALSE;
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
if(A[i, j] &&
(order[j] > order[i]))
Cycles = TRUE;

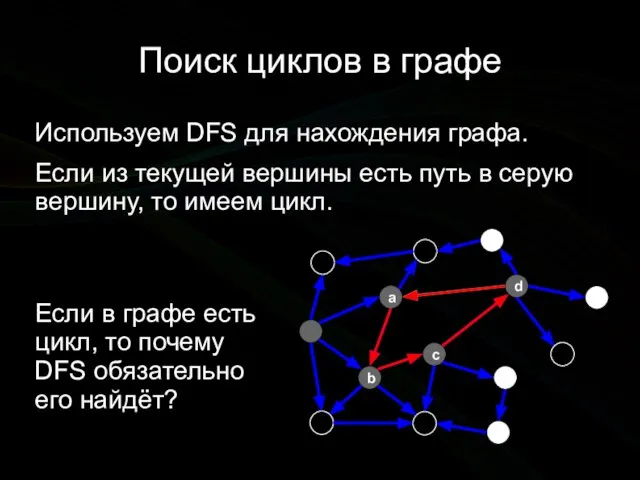
Поиск циклов в графе
Используем DFS для нахождения графа.
Если из текущей вершины есть путь в серую вершину, то имеем цикл.
Если в графе есть цикл, то почему DFS обязательно его найдёт?

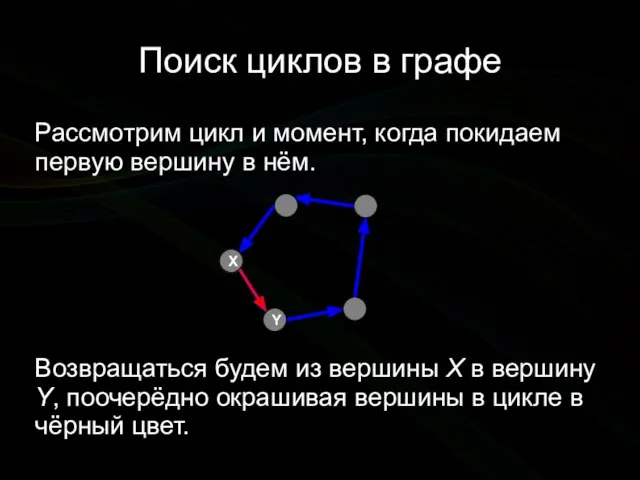
Поиск циклов в графе
Рассмотрим цикл и момент, когда покидаем первую вершину в нём.
Возвращаться будем из вершины X в вершину Y, поочерёдно окрашивая вершины в цикле в чёрный цвет.

Поиск циклов в графе
Как определить сам цикл?
Сделаем стек. При заходе в вершину помещаем её в стек, при выходе — забираем её оттуда.
массив stack длины n — стек вершин;
sp — указатель вершины стека (число элементов в нём).
Pascal
sp := 0;
Push(v):
Inc(sp);
stack[sp] := v;
Pop:
Dec(sp);
C
sp = 0;
Push(v):
stack[++sp - 1] = v;
Pop:
sp--;

Поиск циклов в графе
Pascal
for i := 1 to n do
color[i] := WHITE;
rm := False; found := False; DFS(1);
DFS(v):
color[v] := GRAY; Push(v);
for
do
if not Found then
if color[u] = WHITE then
DFS(u)
else
if color[u] = GRAY then
begin
Found := True;
cc := u; rm := True;
end;
if Found then
<запомнить текущую вершину>;
color[v] := BLACK; Pop;
C
for(i = 0; i < n; i++)
color[i] = WHITE;
rm = Found = FALSE; DFS(0);
DFS(v):
color[v] = GRAY; Push(v);
for(
)
if(!Found)
if(color[u] == WHITE)
DFS(u);
else
if(color[u] == GRAY)
{
rm = Found = TRUE;
cc = u;
};
if(Found)
<запомнить текущую вершину>;
color[v] = BLACK; Pop;

Поиск циклов в графе
Как запомнить все вершины, из которых выходим?
Сделаем второй стек. Если цикл найден, то помещаем во второй стек все покидаемые вершины, пока не встретим вершину cc.
массив stack2 длины n — стек вершин в прямом порядке;
sp2 — указатель вершины второго стека.
Pascal
sp2 := 0;
<запомнить текущую вершину>:
if rm then
begin
rm := rm and (v <> cc);
Inc(sp2); stack2[sp2] := v;
end;
C
sp2 = 0;
<запомнить текущую вершину>:
if(rm)
{
rm &= v != cc;
stack[++sp - 1] = v;
};

Поиск циклов в графе
В первой строке файла input.txt заданы целые n и m — соответственно число вершин и число рёбер ориентированного графа (1 ≤ n ≤ 10 000, 0 ≤ m ≤ 50 000). В следующих m строках файла заданы пары номеров вершин, соединённых рёбрами.
В файл output.txt вывести последовательность номеров вершин, соответствующих любому циклу в графе. Если граф ациклический, то вывести 0.
Ограничение по времени — 1 сек.
Ограничение по памяти — 16 Мб.