Слайд 2Неравномерный код
Если заданы четыре сообщения А1, А2, А3, А4 с вероятностями
Р(А1)=1/2,
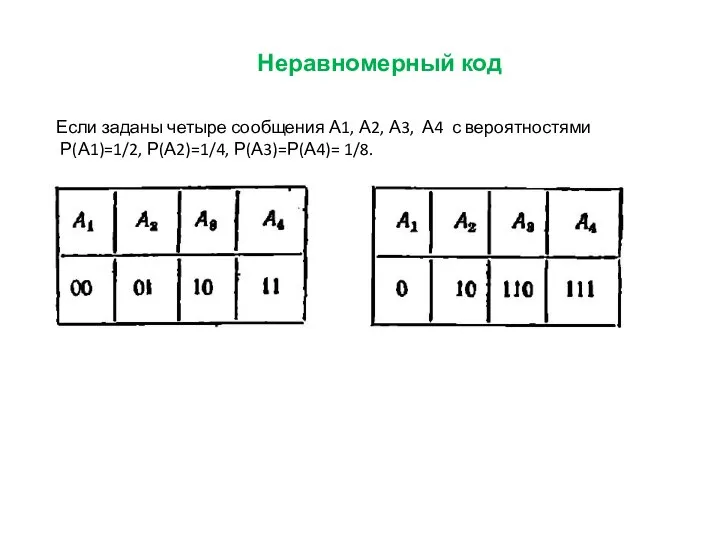
Р(А2)=1/4, Р(А3)=Р(А4)= 1/8.
Слайд 3Идея метода Шеннона-Фано
Идея этого метода заключалась в том, чтобы заменить часто встречающиеся

символы более короткими кодами, а редко встречающиеся последовательности более длинными кодами.
Метод Шеннона-Фано относится к вероятностным методам сжатия
Слайд 5Если заданы четыре сообщения А1, А2, А3, А4 с вероятностями
Р(А1)=1/2, Р(А2)=1/4,
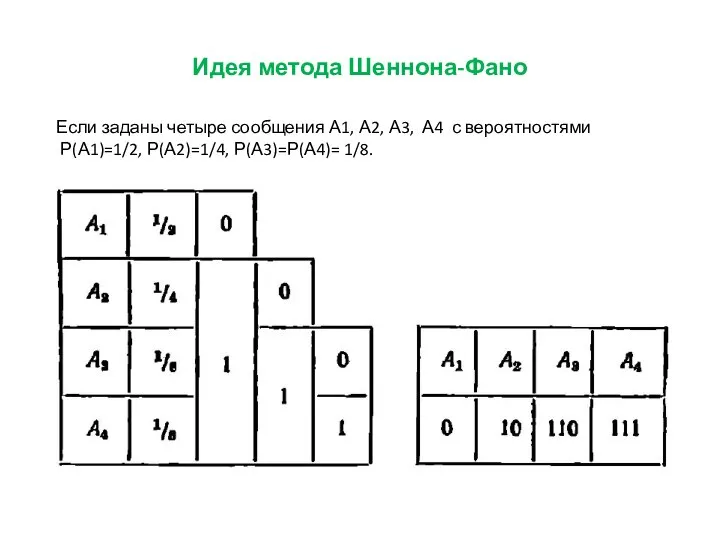
Р(А3)=Р(А4)= 1/8.
Идея метода Шеннона-Фано
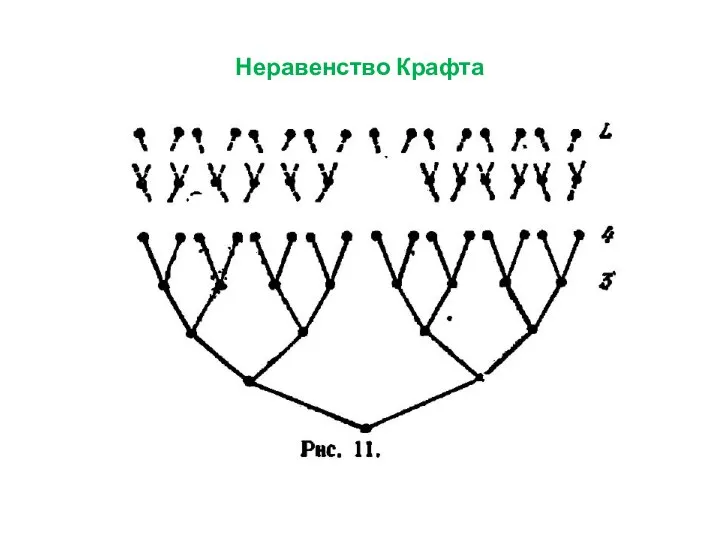
Слайд 7Кодовые деревья
Чем более вероятно сообщение, тем быстрее оно образует «самостоятельную» группу и
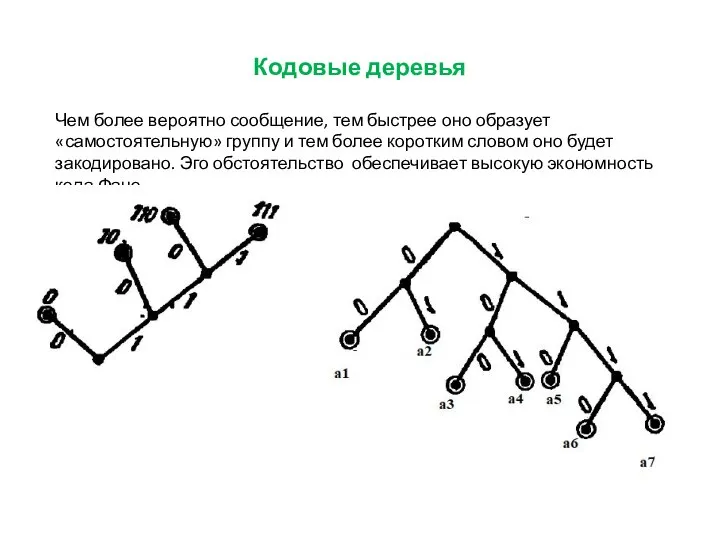
тем более коротким словом оно будет закодировано. Эго обстоятельство обеспечивает высокую экономность кода Фано.
Слайд 8Кодовые деревья
В любом кодовом тексте выделять отдельные кодовые слова без использования специальных

разделительных знаков.
Чтобы код удовлетворял следующему требованию:
- всякая последовательность кодовых символов может быть единственным образом разбита на кодовые слова
Коды для которых последнее требование выполнено,
называются однозначно декодируемыми (иногда их называют
кодами без зanятой).
Наиболее простыми и употребимыми кодами без запятой являются так называемые nрефuкcные коды, обладающие тем свойством. что никакое кодовое слово не является началом (префиксом) другого кодового слова. Если код префиксный, то, читая кодовую запись подряд от начала. мы всегда сможем
разобраться, где кончается одно кодовое слово и начинается следующее.
Слайд 9Префиксный код
Префиксный код называется полным если добавление к нему нового слова не
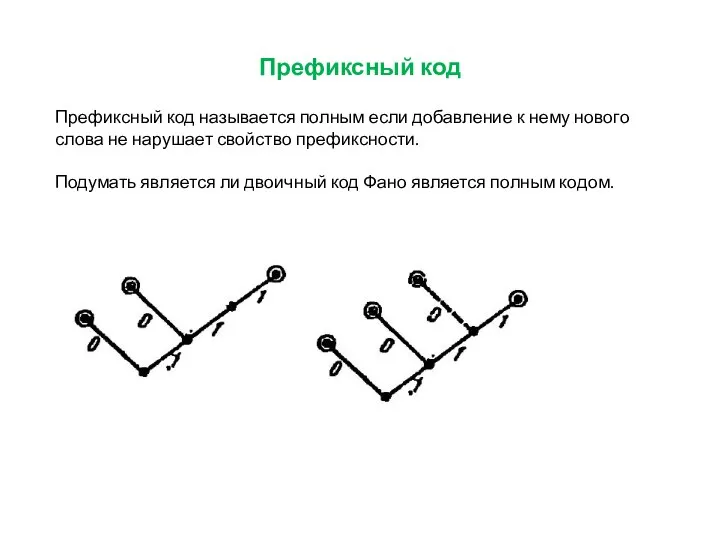
нарушает свойство префиксности.
Подумать является ли двоичный код Фано является полным кодом.
Слайд 10Однозначно декодируемый код, который не является префиксным
{1,10}, {01, 10, 011}
Не существует

префиксного кода с длинами кодовых слов 1,1,2.
Существует ли префиксный код с заданными длинами слов?
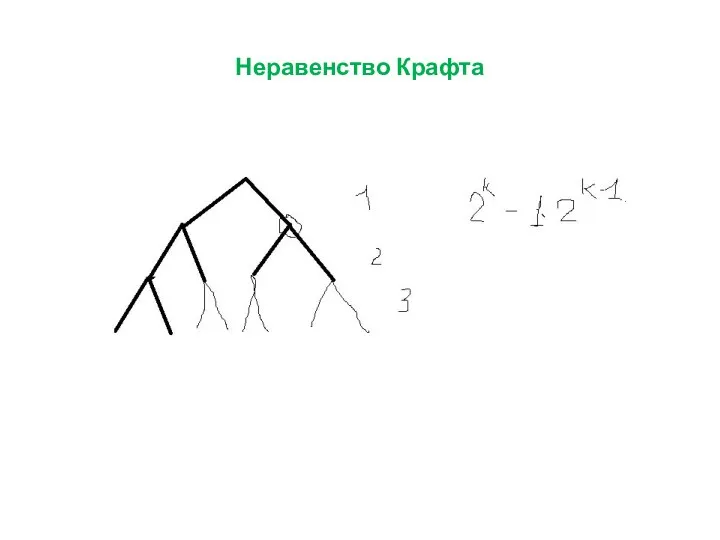
Слайд 22Метод Шеннона построения префиксного кода с заданными длинами слов

Слайд 23Метод Шеннона построения префиксного кода с заданными длинами слов

Слайд 24Метод Шеннона построения префиксного кода с заданными длинами слов

Слайд 25Метод Шеннона построения префиксного кода с заданными длинами слов


































 Онлайн или не онлайн – вот в чем вопрос
Онлайн или не онлайн – вот в чем вопрос Цикл зрелости технологий
Цикл зрелости технологий Информационная система (ИС) медпункта вуза
Информационная система (ИС) медпункта вуза Работа с эффектами наведения курсора CSS
Работа с эффектами наведения курсора CSS Фотогравировка
Фотогравировка SCADA система RIVG
SCADA система RIVG
 Моделирование фартука с помощью графического редактора Paint
Моделирование фартука с помощью графического редактора Paint Проект. Система внутрикорпоративных коммуникаций (ВКК): диагностика и оптимизация
Проект. Система внутрикорпоративных коммуникаций (ВКК): диагностика и оптимизация Миграция для Notes в Exchange
Миграция для Notes в Exchange PHP. Разработка блога. Часть 2. Урок 8
PHP. Разработка блога. Часть 2. Урок 8 Мир социальных сетей
Мир социальных сетей Технология программирования на языке python и разработка программ для машинного обучения
Технология программирования на языке python и разработка программ для машинного обучения The concept of information technology
The concept of information technology Функции в С++
Функции в С++ Кейс: ООО Флагман-Пресс. Юные герои сороковых, пороховых
Кейс: ООО Флагман-Пресс. Юные герои сороковых, пороховых Проект “Аналитик”
Проект “Аналитик” Bizneskeis — маркетинговый клуб
Bizneskeis — маркетинговый клуб Программное обеспечение ПК
Программное обеспечение ПК Таблицы как средство моделирования
Таблицы как средство моделирования Цифровые технологии
Цифровые технологии Интернет-зависимость и социокультурные предпосылки её возникновения
Интернет-зависимость и социокультурные предпосылки её возникновения 5216a7a1dec15e0e (1)
5216a7a1dec15e0e (1) Способы настройки IPV6
Способы настройки IPV6 Решение задач на компьютере алгоритмизация и программирование
Решение задач на компьютере алгоритмизация и программирование Программы перевода из одной системы счисления в другую
Программы перевода из одной системы счисления в другую Обработка графики
Обработка графики StyleOut. Создание сайта и его оформление
StyleOut. Создание сайта и его оформление