Сортировка массивов

План
Сортировка с помощью прямого включения
Сортировка с помощью прямого выбора
Сортировка с помощью прямого обмена (пузырьковая)
Улучшенный метод пузырька
Сортировка с помощью разделения (быстрая)

1. Сортировка методом прямого включения
Такой метод широко используется при игре в карты. Элементы (карты) мысленно делятся на уже "готовую" последовательность а1... ai-1 и исходную последовательность а1... an.
При каждом шаге, начиная с i = 2 и увеличивая i каждый раз на единицу, из исходной последовательности извлекается i-й элемент и перекладывается в готовую последовательность, при этом он вставляется в нужное место.

1. Сортировка с помощью прямого включения
Алгоритм этой сортировки таков:
for (i=1; i
{ х= a[i];
включение х на соответствующее место
среди а[0] ... а[i-1];
}

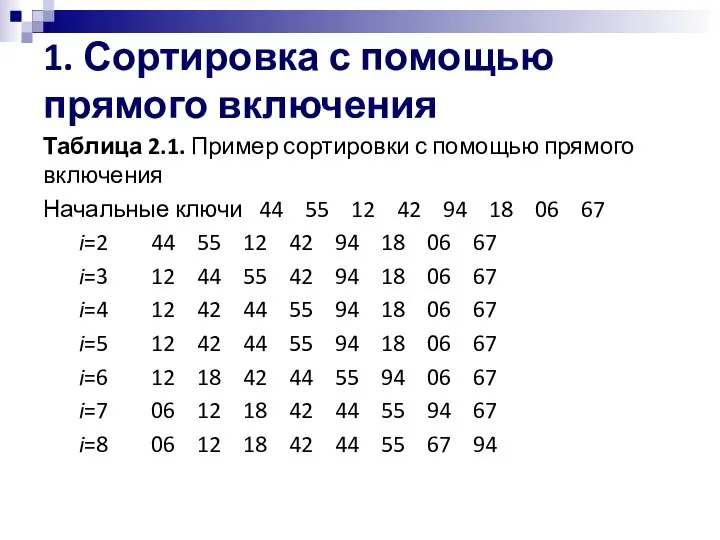
1. Сортировка с помощью прямого включения
Таблица 2.1. Пример сортировки с помощью прямого включения
Начальные ключи 44 55 12 42 94 18 06 67
i=2 44 55 12 42 94 18 06 67
i=3 12 44 55 42 94 18 06 67
i=4 12 42 44 55 94 18 06 67
i=5 12 42 44 55 94 18 06 67
i=6 12 18 42 44 55 94 06 67
i=7 06 12 18 42 44 55 94 67
i=8 06 12 18 42 44 55 67 94

1. Сортировка с помощью прямого включения
В реальном процессе поиска подходящего места удобно, чередуя сравнения и движения по последовательности, как бы просеивать x, т. е. х сравнивается с очередным элементом aj, а затем либо х вставляется на свободное место, либо aj сдвигается (передается) вправо, и процесс "уходит" влево. Обратите внимание, что процесс просеивания может закончиться при выполнении одного из двух следующих различных условий:
1. Найден элемент aj с ключом, меньшим чем ключ у х.
2. Достигнут левый конец готовой последовательности.

1. Сортировка с помощью прямого включения
Такой типичный случай повторяющегося процесса с двумя условиями окончания позволяет нам воспользоваться хорошо известным приемом барьера (sentinel). Здесь его легко применить, поставив барьер a0 со значением х. (Заметим, что для этого необходимо расширить диапазон индекса в описании переменной 0...n). Полный алгоритм приводится в листинге 2.1*.

1. Сортировка с помощью прямого включения
for (i=1;i
{
int x=a[i];
j=i; while (x
0)
{
a[j]=a[j-1]; j--;
}
a[j]=x;
}

1. Сортировка с помощью прямого включения
Стоит отметить, что приведенная программа не совсем соответствует естественному ходу мышления при ее построение Естественным кажется вести поиск не влево от очередного просматриваемого элемента, а с самого начала готовой последовательности. При этом и барьер специально ставить нет нужды.

2. Сортировка методом прямого выбора
1. Выбирается элемент с наименьшим ключом.
2. Он меняется местами с первым элементом.
3. Затем этот процесс повторяется с оставшимися n- 1 элементами, n - 2 элементами и т. д. до тех пор, пока не останется один, самый большой элемент.

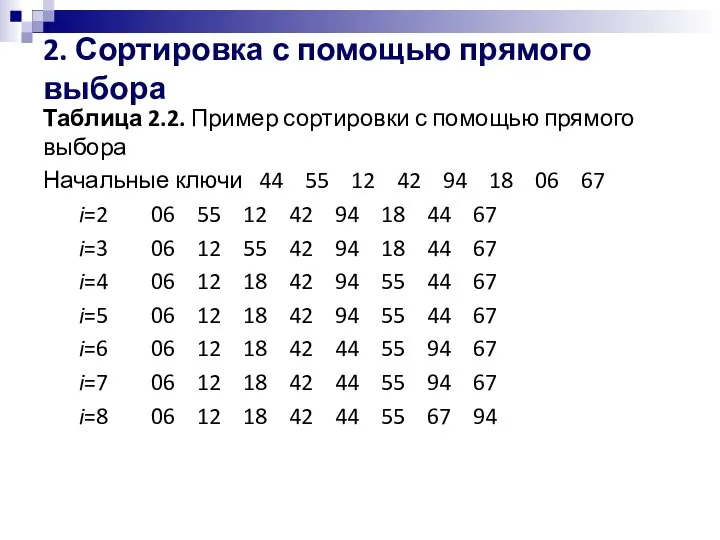
2. Сортировка с помощью прямого выбора
Процесс работы этим методом с теми же восемью ключами, что и в табл. 2.1, иллюстрирует табл. 2.2. Алгоритм формулируется следующим образом:
for (i=0; i
{
присвоить k индекс наименьшего из a[i] ... а[n-1];
поменять местами a[i] u a[k];
}

2. Сортировка с помощью прямого выбора
Таблица 2.2. Пример сортировки с помощью прямого выбора
Начальные ключи 44 55 12 42 94 18 06 67
i=2 06 55 12 42 94 18 44 67
i=3 06 12 55 42 94 18 44 67
i=4 06 12 18 42 94 55 44 67
i=5 06 12 18 42 94 55 44 67
i=6 06 12 18 42 44 55 94 67
i=7 06 12 18 42 44 55 94 67
i=8 06 12 18 42 44 55 67 94

2. Сортировка с помощью прямого выбора
Такой метод - его называют прямым выбором - в некотором смысле противоположен прямому включению. При прямом включении на каждом шаге рассматриваются только один очередной элемент исходной последовательности и все элементы готе последовательности, среди которых отыскивается точка включения; при прямом выборе для поиска одного элемента с наименьшим ключом просматриваются все элементы исходной последовательности и найденный помещается как очередной элемент готовую последовательность. Полностью алгоритм прямого выбора приводится в листинге 2.3.

2. Сортировка с помощью прямого выбора
for (i=0;i<(n-1);i++)
{
int k=i, x=a[i]; for (j=i+1; j
if (a[j]
{
k=j;
x=a[k];
}
a[k]=a[i]; a[i]=x;
}

3. Сортировка методом прямого обмена
Классификация методов сортировки редко бывает осмысленной. Оба разбиравшихся до этого метода можно тоже рассматривать как "обменные" сортировки. Однако в данном разделе мы опишем метод, где обмен местами двух элементов представляет собой характернейшую особенность процесса. Изложенный ниже а. ритм прямого обмена основывается на сравнении и смене мест для пары соседних элементов и продолжении этого процесс тех пор, пока не будут упорядочены все элементы.

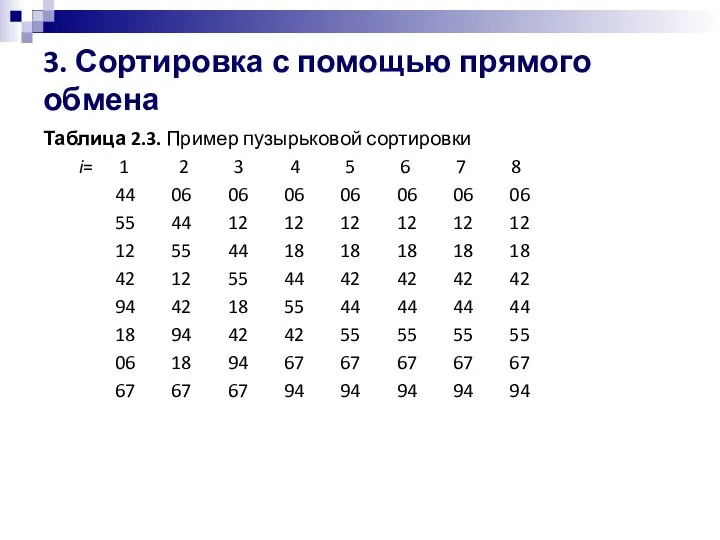
3. Сортировка с помощью прямого обмена
Таблица 2.3. Пример пузырьковой сортировки
i= 1 2 3 4 5 6 7 8
44 06 06 06 06 06 06 06
55 44 12 12 12 12 12 12
12 55 44 18 18 18 18 18
42 12 55 44 42 42 42 42
94 42 18 55 44 44 44 44
18 94 42 42 55 55 55 55
06 18 94 67 67 67 67 67
67 67 67 94 94 94 94 94

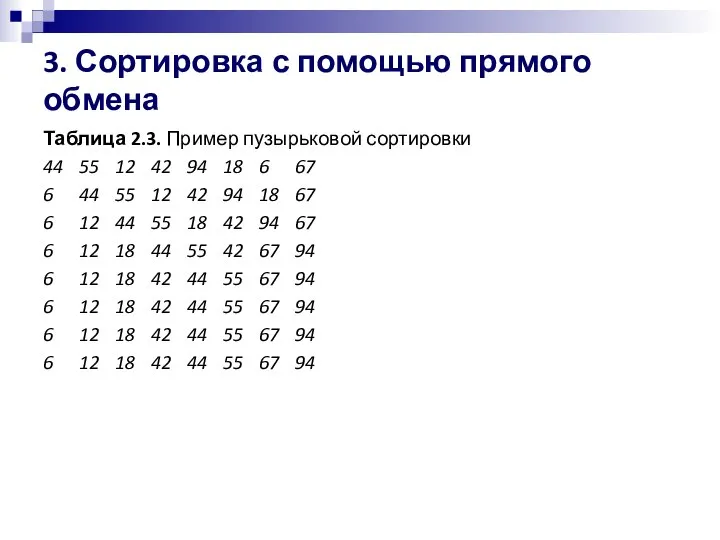
3. Сортировка с помощью прямого обмена
Таблица 2.3. Пример пузырьковой сортировки
44 55 12 42 94 18 6 67
6 44 55 12 42 94 18 67
6 12 44 55 18 42 94 67
6 12 18 44 55 42 67 94
6 12 18 42 44 55 67 94
6 12 18 42 44 55 67 94
6 12 18 42 44 55 67 94
6 12 18 42 44 55 67 94

3. Сортировка с помощью прямого обмена
Как и в упоминавшемся методе прямого выбора, мы повтор проходы по массиву, сдвигая каждый раз наименьший элемент, оставшейся последовательности к левому концу массива, если будем рассматривать массивы как вертикальные, а не горизонтальные построения, то элементы можно интерпретировать как пузырьки в чане с водой, причем вес каждого соответствует его ключу. В этом случае при каждом проходе один пузырек как бы поднимается до уровня, соответствующего его весу (см. табл.) Такой метод широко известен под именем пузырьковая сортировка.

3. Сортировка с помощью прямого обмена
for (i=1;i
for (j=(n-1);j>=i;j--)
if (a[j-1]>a[j])
{ x=a[j-1];
a[j-1]=a[j];
a[j]=x;
}

4. Улучшенный метод пузырька
Очевидный прием улучшения этого алгоритма - запоминать, были или не были перестановки в процессе некоторого прохода. Если в последнем проходе перестановок не было, то алгоритм можно заканчивать.

4. Улучшенный метод пузырька
Это улучшение, однако, можно опять же улучшить, если запоминать не только сам факт, что обмен имел место, но и положение (индекс) последнего обмена. Ясно, что все пары соседних элементов выше этого индекса k уже находятся в желаемом порядке. Поэтому просмотры можно заканчивать на этом индексе, а не идти до заранее определенного нижнего предела

4. Улучшенный метод пузырька
Внимательный программист заметит здесь некоторую своеобразную асимметрию. Один плохо расположенный пузырек на "тяжелом конце" в массиве с обратным порядком будет перемещаться на нужное место в один проход, но плохо расположенный элемент на "легком конце" будет просачиваться на свое нужное место на один шаг при каждом проходе. Например, массив
12 18 42 44 55 67 94 06
с помощью усовершенствованной пузырьковой сортировки можно упорядочить за один просмотр, а для сортировки массива
94 06 12 18 42 44 55 67
требуется семь просмотров. Такая неестественная симметрия наводит на мысль о третьем улучшении: чередовать направление последовательных просмотров.

4. Улучшенный метод пузырька
Получающийся при этом алгоритм назовем шейкернои* сортировкой (ShakerSort).
L = 2 3 3 4 4
R = 8 8 8 7 7
Dir = ↑ ↓ ↑ ↓ ↑
44 06 06 06 06
55 44 44 12 12
12 55 12 44 18
42 12 42 18 42
94 42 55 42 44
18 94 18 55 55
06 18 67 67 67
67 67 94 94 94

4. Улучшенный метод пузырька
int L,R,k; L=1; R=n-1; k=n-1;
do {
for (j=R; j>=L; j--)
if (a[j-1]>a[j]) {
x=a[j-1]; a[j-1]=a[j]; a[j]=x; k=j;
}
L=k+1;
for (j=L; j<=R; j++)
if (a[j-1]>a[j]) {
x=a[j-1]; a[j-1]=a[j]; a[j]=x; k=j;
}
R=k-1;
}
while (L<=R);

5. Сортировка методом разделения (быстрая)
Разобравшись в двух усовершенствованных методах сортировки, построенных на принципах включения и выбора, мы тепе коснемся третьего улучшенного метода, основанного на обмене. Если учесть, что пузырьковая сортировка в среднем была самой неэффективной из всех трех алгоритмов прямой (строгой) сортировки, то следует ожидать относительно существенного улучшения. И все же это выглядит как некий сюрприз: улучшение метода, основанного на обмене, о котором мы будем сейчас говорить, оказывается, приводит к самому лучшему из известных в данный момент методу сортировки для массивов. Его производительность столь впечатляюща, что изобретатель Ч. Хоар даже назвал метод быстрой сортировкой (Quicksort).

5. Сортировка с помощью разделения (быстрая)
В Quicksort исходят из того соображения, что для достижения наилучшей эффективности сначала лучше производить перестановки на большие расстояния. Предположим, у нас есть n элементов, расположенных по ключам в обратном порядке. Их можно отсортировать за n/2 обменов: сначала поменять местами самый левый с самым правым, а затем последовательно двигаться с двух сторон. Конечно, это возможно только в том случае, когда мы знаем, что порядок действительно обратный. Но из этого примера можно извлечь и нечто действительно поучительное.

5. Сортировка с помощью разделения (быстрая)
Алгоритмом:
выберем наугад какой-либо элемент (назовем его х) и будем просматривать слева наш массив до тех пор, пока не обнаружим элемент aj > х, затем будем просматривать массив справа, пока не встретим aj < х. Теперь поменяем местами эти два элемента и продолжим наш процесс просмотра и обмена, пока оба просмотра не встретятся где-то в середине массива. В результате массив окажется разбитым на левую часть, с ключами меньше (или равными) х, и правую - с ключами больше (или равными) х.

5. Сортировка с помощью разделения (быстрая)
int i=0; int j=n-1;
float middle=arr[(left+right)/2]; while (i
while (arr[i]
while (middle
if (i<=j) {
float temp=arr[i]; arr[i]=arr[j]; arr[j]=temp;
i++; j--;
}
}

5. Сортировка с помощью разделения (быстрая)
Обратите внимание, что вместо отношений > и < используются >= и =<, а в заголовке цикла с WHILE — их отрицание < и >. При таких изменениях х выступает в роли барьера для того и другого просмотра. Если взять в качестве х для сравнения средний ключ 42, то в массиве ключей
44 55 12 42 94 06 18 67
для разделения понадобятся два обмена: 18 ↔ 44 и 6 ↔ 55
18 06 12 42 94 55 44 67

5. Сортировка с помощью разделения (быстрая)
Последние значения индексов таковы: i=5, a j=3. Ключи а1,...аi-1 меньше или равны ключу х = 42, а ключи aj+1,...,аn больше равны х. Следовательно, существует две части, а именно:
Ak: 1<=k
Ak :j

5. Сортировка с помощью разделения (быстрая)
Описанный алгоритм очень прост и эффективен, поскольку главные сравниваемые величины i, j и х можно хранить во время просмотра в быстрых регистрах машины. Однако он может оказаться и неудачным, что, например, происходит в случае п идентичных ключей: для разделения нужно n/2 обменов. Этих вовсе необязательных обменов можно избежать, если операторы просмотра заменить на такие:
while (arr[i]
while (middle

5. Сортировка с помощью разделения (быстрая)
Однако в этом случае выбранный элемент х, находящийся среди компонент массива, уже не работает как барьер для двух просмотров. В результате просмотры массива со всеми идентичными ключами приведут, если только не использовать более сложные условия их окончания, к переходу через границы массива. Простота условий, употребленных в листинге 2.9, вполне оправдывает те дополнительные обмены, которые происходят в среднем относительно редко. Можно еще немного сэкономить, если изменить заголовок, управляющий самим обменом: от i <= j перейти к i < j Однако это изменение не должно касаться двух операторов: i:=i+1; j:=j-1. Поэтому для них потребуется отдельный условный оператор.

5. Сортировка с помощью разделения (быстрая)
Теперь напомним, что наша цель — не только провести разделение на части исходного массива элементов, но и отсортировать его. Сортировку от разделения отделяет, однако, лишь небольшой шаг: нужно применить этот процесс к получившимся двум частям, затем — к частям частей, и так до тех пор, пока каждая из частей не будет состоять из одного-единственного элемента. Эти действия описываются листингом 2.10.