Содержание
- 2. Пропозициональная логика - это раздел фрагмент логики, в котором новые операторы строятся из заданных операторов, используя
- 3. Высказыванием называется любое повествовательное предложение, про которое известно, что оно или истинно, или ложно. Вопросительные, повелительные
- 4. Например: Слоны летят на север. - Ложное высказывание. Треугольник - это геометрическая фигура. - Истинное высказывание
- 5. Высказывание считается простым, если никакую его часть нельзя рассматривать как отдельное высказывание Высказывание, которое можно разложить
- 6. В математической логике высказывания обозначают большими латинскими буквами. Например: А = Новосибирск – не столица России.
- 7. Простые высказывания называются логическими переменными Например: А = «Луна является спутником Земли.» → А = 1
- 8. Сложные высказывания называются логическими формулами или логическими функциями, Значение логической функции может принимать значения только 0
- 9. Составные (сложные) высказывания строятся из простых с помощью логических связок: "и« ∧, "или« ∨, "не", ¬
- 10. I. ОПЕРАЦИЯ – ЛОГИЧЕСКОЕ УМНОЖЕНИЕ Объединение двух (или нескольких) высказываний в одно при помощи союза «и»
- 11. Высказывание вида A & B (А конъюнкция B ) истинно тогда и только тогда, когда истинны
- 12. II. ОПЕРАЦИЯ – ЛОГИЧЕСКОЕ СЛОЖЕНИЕ Объединение двух (или нескольких) высказываний в одно при помощи союза «или»
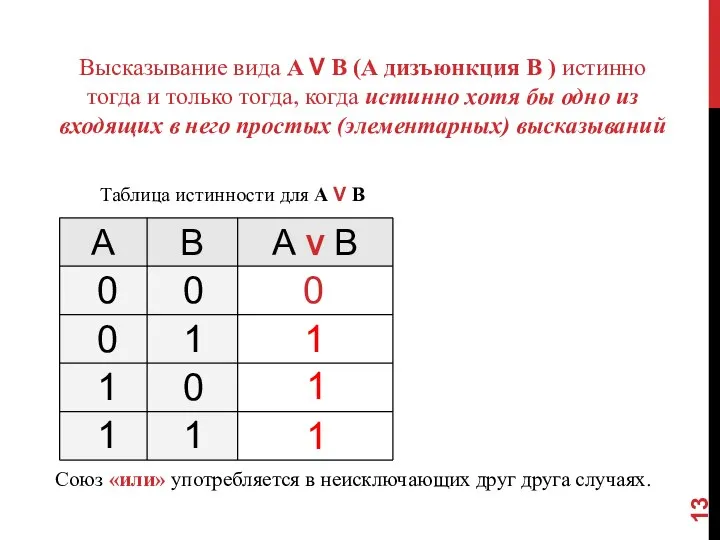
- 13. Высказывание вида A V B (А дизъюнкция B ) истинно тогда и только тогда, когда истинно
- 14. III. ОПЕРАЦИЯ – ЛОГИЧЕСКОЕ ОТРИЦАНИЕ Присоединение частицы «не» к высказыванию называется операцией логического отрицания или инверсией
- 15. Высказывание вида Ā (инверсия А) делает истинное высказывание ложным и , наоборот, ложное - истинным Например
- 16. IV. ОПЕРАЦИЯ – ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ Объединение двух высказываний с помощью оборота речи «если …, то …»
- 17. Высказывание вида A → B (А импликация B ) ложно тогда и только тогда, когда А
- 18. V. ОПЕРАЦИЯ – ЛОГИЧЕСКОЕ РАВЕНСТВО Объединение двух высказываний с помощью оборота речи «…тогда и только тогда,
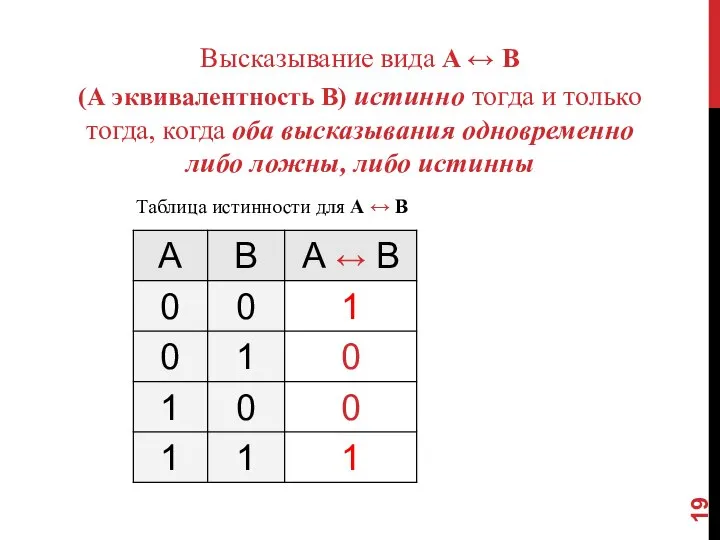
- 19. Высказывание вида A ↔ B (А эквивалентность B) истинно тогда и только тогда, когда оба высказывания
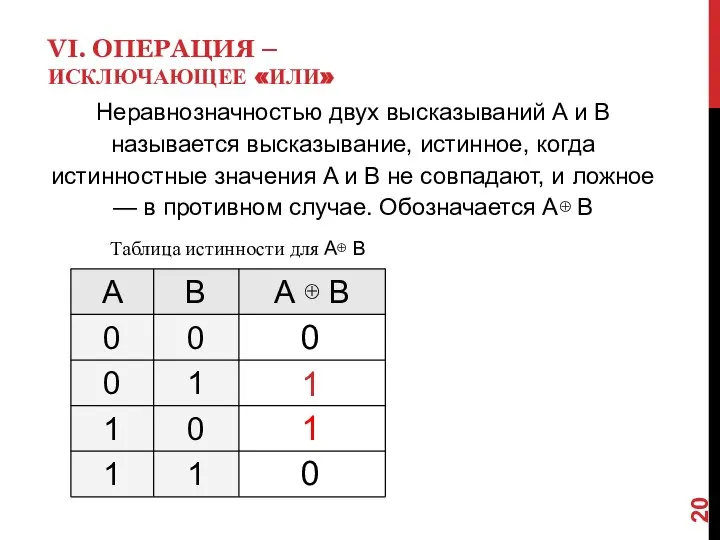
- 20. VI. ОПЕРАЦИЯ – ИСКЛЮЧАЮЩЕЕ «ИЛИ» Неравнозначностью двух высказываний A и B называется высказывание, истинное, когда истинностные
- 21. VII. ОПЕРАЦИЯ – ШТРИХ ШЕФФЕРА Логическая операция А|В, которая ложна, когда оба выражения - истина. Таблица
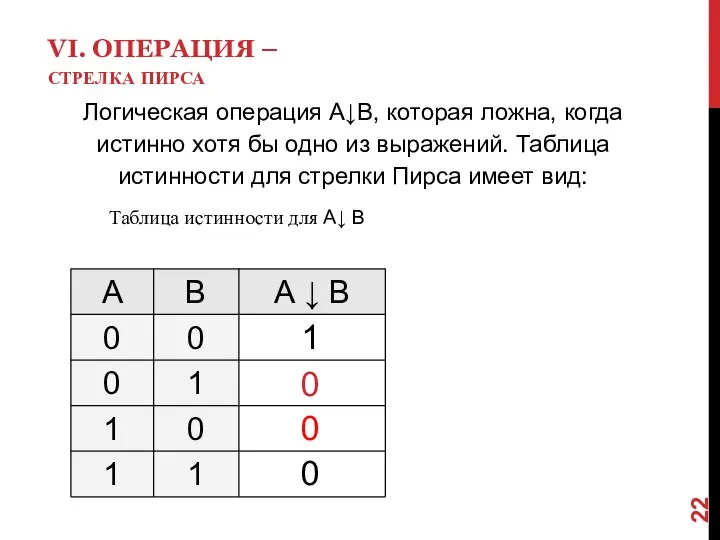
- 22. VI. ОПЕРАЦИЯ – СТРЕЛКА ПИРСА Логическая операция А↓В, которая ложна, когда истинно хотя бы одно из
- 23. Применяя логические операции, можно построить и решить логические выражения или логические формулы: Для построения простые логические
- 24. Например: Для определения значения логической функции необходимо помнить порядок выполнения логических операций по иерархии Такая запись
- 25. Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке: 1. ( )
- 26. Для построения таблицы истинности любой логической функции следует соблюдать: 1. определить кол-во строк таблицы – 2n
- 27. Для построения таблицы истинности любой логической функции следует соблюдать: 3. построить таблицу истинности с найденным кол-вом
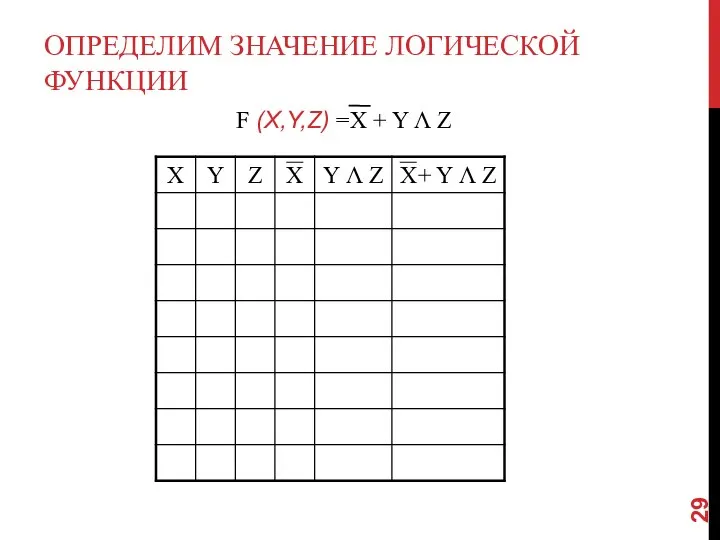
- 28. Количество входных переменных равно трем (X,Y,Z), а значит строк Q= 23 = 8 +1 =9 (заголовки
- 29. ОПРЕДЕЛИМ ЗНАЧЕНИЕ ЛОГИЧЕСКОЙ ФУНКЦИИ
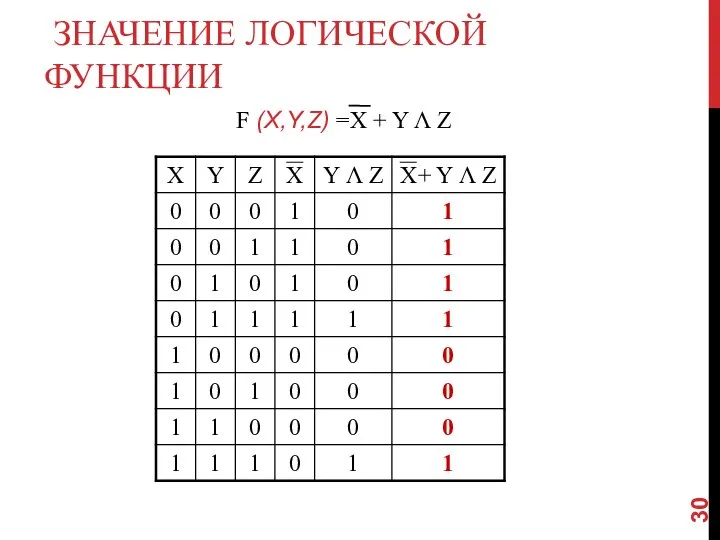
- 30. ЗНАЧЕНИЕ ЛОГИЧЕСКОЙ ФУНКЦИИ
- 31. Математическая логика - решение задач
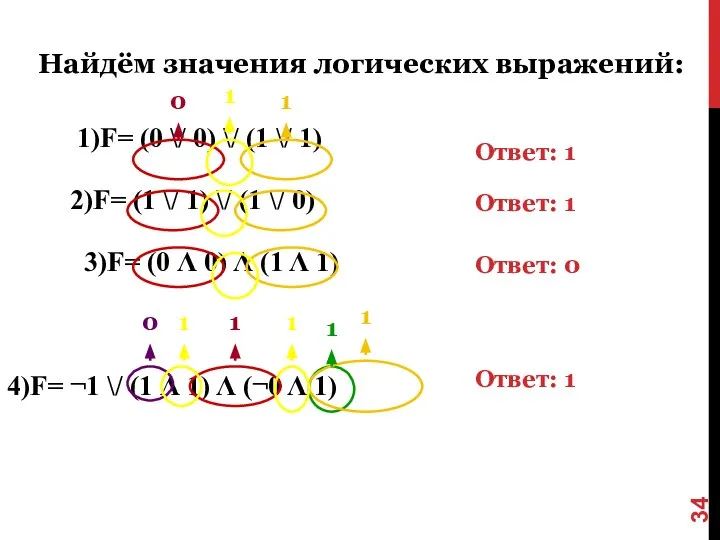
- 32. 1)F= (0 \/ 0) \/ (1 \/ 1) 2)F= (1 \/ 1) \/ (1 \/ 0)
- 33. 1)F= (0 \/ 0) \/ (1 \/ 1) 2)F= (1 \/ 1) \/ (1 \/ 0)
- 34. 1)F= (0 \/ 0) \/ (1 \/ 1) 2)F= (1 \/ 1) \/ (1 \/ 0)
- 35. Для какого из указанных значений числа X истинно высказывание ¬((X > 3) → (X > 4))
- 37. Скачать презентацию



























 Решение задач. Таблицы истинности. Комбинаторика. Делимость и конъюкция
Решение задач. Таблицы истинности. Комбинаторика. Делимость и конъюкция Информационные технологии
Информационные технологии Презентация на тему Основы моделирования
Презентация на тему Основы моделирования  Одномерные массивы целых чисел. Начала программирования. 9 класс
Одномерные массивы целых чисел. Начала программирования. 9 класс Криптография и стенография
Криптография и стенография Мастер-класс работа в Photoshop
Мастер-класс работа в Photoshop Разработка сайта-музея военного аэродрома Арктика
Разработка сайта-музея военного аэродрома Арктика Обработка символьной информации в языке Pascal
Обработка символьной информации в языке Pascal Итерационные алгоритмы и программы. Лекция 7
Итерационные алгоритмы и программы. Лекция 7 1111111111111111111111111
1111111111111111111111111 Computers in unserem leben
Computers in unserem leben Профессиональное прикладное программное обеспечение логистической деятельности
Профессиональное прикладное программное обеспечение логистической деятельности Фиксация оригиналов первичных документов
Фиксация оригиналов первичных документов Клиент-серверная web-система для распространения билетов в театр
Клиент-серверная web-система для распространения билетов в театр Создание текста в документе Microsoft Word. Урок 3
Создание текста в документе Microsoft Word. Урок 3 Работа в слоях
Работа в слоях Реляционная модель базы данных
Реляционная модель базы данных Информация. Информационная грамотность. Информационная культура
Информация. Информационная грамотность. Информационная культура Правила безопасного поведения в Интернете
Правила безопасного поведения в Интернете Sortirovka_Massiva_abdrakhmanova
Sortirovka_Massiva_abdrakhmanova Блок управления GDS-II - новые возможности
Блок управления GDS-II - новые возможности Ukrainian radiation equipment. Украинское радиационное оборудование
Ukrainian radiation equipment. Украинское радиационное оборудование Игра Что? Где? Сколько?
Игра Что? Где? Сколько? Системы автоматизированного проектирования (САПР)
Системы автоматизированного проектирования (САПР) Программирование в виде релейно-контактных схем
Программирование в виде релейно-контактных схем Tables – таблицы
Tables – таблицы Защита информации в компьютерных системах
Защита информации в компьютерных системах Презентация на тему Число и кодирование информации
Презентация на тему Число и кодирование информации