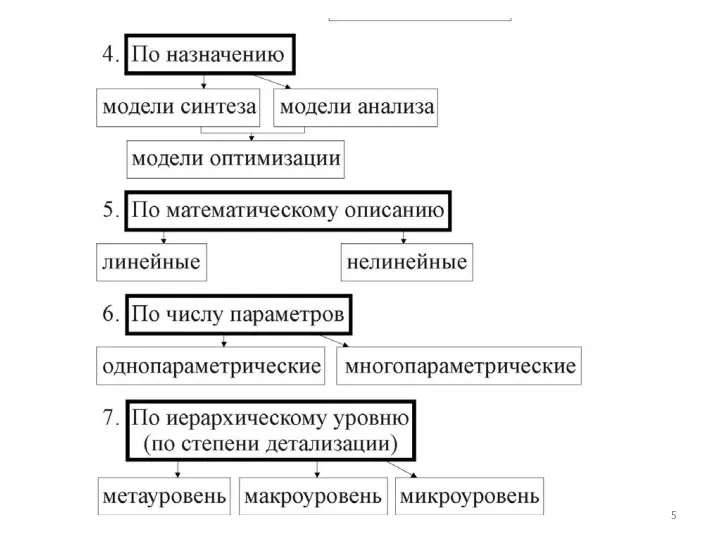
Содержание
- 2. Моделированием называется процесс изучения реального объекта, проводимый не на самом объекте, а на его модели. Модель
- 3. Под объектом или системой моделирования обычно понимается совокупность предметов, как реальных, так и идеальных, которая организована
- 6. Математические модели позволяют количественно исследовать явления, трудно поддающиеся изучению на физических моделях. Вероятностная модель – это
- 7. Исходные данные Имеется массив объектов с наблюдаемыми переменными X и скрытыми переменными T Предполагается, что между
- 8. При вероятностном подходе к решению задач, неопределенность в зависимости между X и T моделируется введением совместного
- 9. При использовании порождающих моделей необходимо задать совместное распределение p(X, T) на множестве объектов Зная совместное распределение
- 10. При использовании дискримина-тивных моделей необходимо знать условное распределение p(T|X) на множестве значений скрытых переменных объекта Зная
- 11. В отличие от порождающей модели, дискриминативная модель не позволяет моделировать новые объекты из генеральной совокупности. Если
- 12. Первый этап математического моделирования постановка задачи, определение объекта и целей исследования, установление границ области влияния изучаемого
- 13. Первый этап математического моделирования Границы области влияния объекта определяются областью значимого взаимодействия с внешними объектами: границы
- 14. Второй этап математического моделирования выбор типа математической модели контроль математической модели Строится несколько моделей, на основе
- 15. Если для формирования математической модели недостаточно исходных данных, то выполняется поисковый эксперимент, в ходе которого устанавливаются:
- 16. Линейность устанавливается по характеру статической характеристики исследуемого объекта. Статическая характеристика объекта - связь между величиной внешнего
- 17. Динамичности или статичности осуществляется по поведению исследуемых показателей объекта во времени. Объект исследования можно считать стационарным,
- 18. Детерминированным называется объект с полностью известными (детерминированными) параметрами. Если хотя бы один параметр неизвестен или является
- 19. Контроль математической модели виды контроля (проверки): размерностей; порядков; характера зависимостей; экстремальных ситуаций; граничных условий; математической замкнутости;
- 20. Контроль размерностей сводится к проверке выполнения правила, согласно которому приравниваться и складываться могут только величины одинаковой
- 21. Анализ экстремальных ситуаций сводится к проверке наглядного смысла решения при приближении параметров модели к нулю или
- 22. Анализ математической замкнутости сводится к проверке того, что ММ дает однозначное решение. Анализ физического смысла сводится
- 23. Характеристика вероятностный математических моделей теоретических распределений, применяемых в решении задач автомобильного транспорта
- 24. Плотность вероятности случайной величины X, такая функция р(х), что при любых a и b вероятность неравенства
- 25. Вероятность безотказной работы - это вероятность того, что в пределах заданий наработки отказ объекта не возникает.
- 26. Средней наработкой до отказа называется математическое ожидание наработки объекта до первого отказа T1. Средняя наработка до
- 27. Интенсивность отказов - это условная плотность вероятности возникновения отказа объекта,определяемая при условии, что до рассматриваемого момента
- 28. Средняя наработка на отказ объекта (наработка на отказ) определяется как отношение суммарной наработки восстанавливаемого объекта к
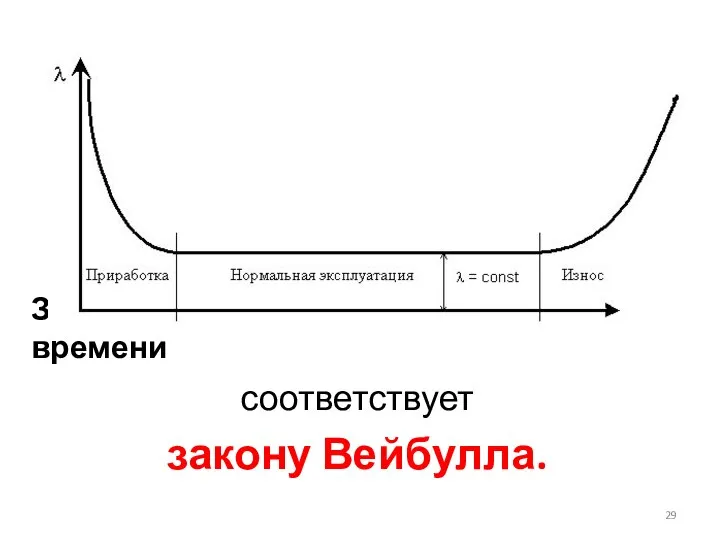
- 29. Зависимость интенсивности отказов от времени соответствует закону Вейбулла.
- 30. Распределение Вейбулла Зависимость интенсивности отказов от времени можно получить, используя для вероятностного описания случайной наработки до
- 31. Распределение Вейбулла где δ - параметр формы (определяется подбором в результате обработки экспериментальных данных, δ >
- 32. Распределение Вейбулла Интенсивность отказов Вероятность безотказной работы
- 33. Распределение Вейбулла Средняя наработки до отказа
- 34. Распределение Вейбулла При параметре δ= 1 распределение Вейбулла переходит в экспоненциальное, а при δ= 2 -
- 35. Распределение Вейбулла Путем подбора параметра δ можно получить, на каждом из трех участков, такую теоретическую кривую
- 36. Экспоненциальное распределение Частный случай распределения Вейбулла, когда параметр формы δ = 1. Распределение однопараметрическое, то есть
- 37. Экспоненциальное распределение Если интенсивность отказов постоянна, то вероятность безотказной работы как функция времени подчиняется экспоненциальному закону:
- 38. Экспоненциальное распределение Среднее время безотказной работы: Вероятность безотказной работы на интервале, превышающем среднее время Т1 будет
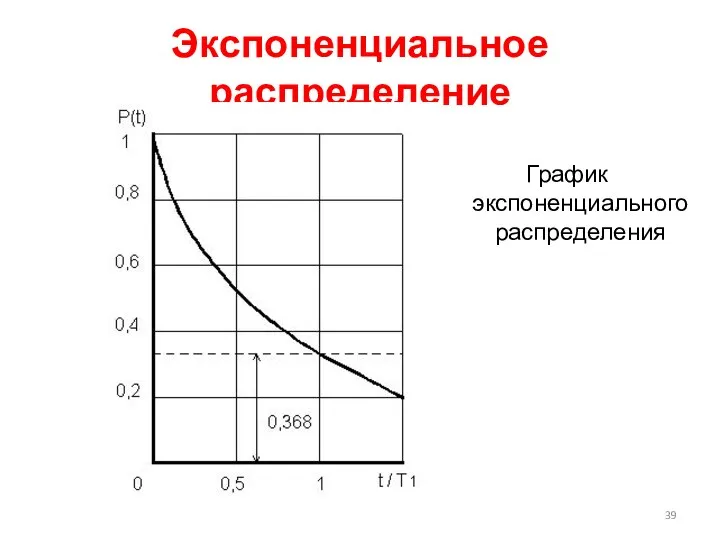
- 39. Экспоненциальное распределение График экспоненциального распределения
- 40. Экспоненциальное распределение Длительность периода нормальной эксплуатации до наступления старения может оказаться существенно меньше Т1, т.е. интервал
- 41. Экспоненциальное распределение Если объект отработал время τ без отказа, сохранив λ = соnst, то дальнейшее распределение
- 42. Экспоненциальное распределение Таким образом, отключение работоспособного объекта в конце интервала и новое его включение на такой
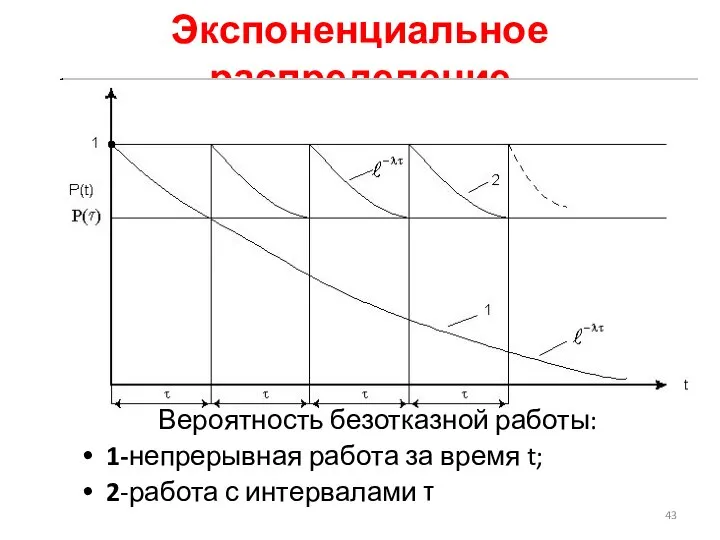
- 43. Экспоненциальное распределение Вероятность безотказной работы: 1-непрерывная работа за время t; 2-работа с интервалами τ
- 44. Нормальное распределение (распределение Гаусса) дает хорошую модель для реальных явлений, в которых: 1) имеется сильная тенденция
- 45. Нормальное распределение Плотностью вероятности где mx, σx - соответственно математическое ожидание и среднеквадратическое отклонение случайной величины
- 46. Нормальное распределение Вероятность безотказной работы интенсивность отказов
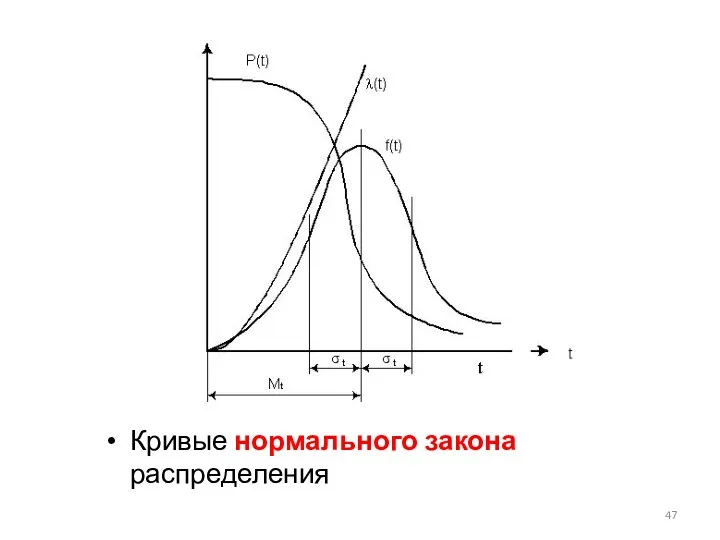
- 47. Кривые нормального закона распределения
- 48. Проверка адекватности моделей т.е. проверка того, насколько хорошо модель описывает реальные процессы, происходящие в системе, насколько
- 49. Проверка адекватности заключается в доказательстве факта, что точность результатов, полученных по модели, будет не хуже точности
- 51. Скачать презентацию











































 Знакомство с языком HTML
Знакомство с языком HTML Система сертификации средств защиты информации
Система сертификации средств защиты информации Презентация на тему Циклический алгоритм
Презентация на тему Циклический алгоритм  CRM система для УрФУ
CRM система для УрФУ Презентация на тему Накопители на жестких магнитных дисках
Презентация на тему Накопители на жестких магнитных дисках  Обеспечение безопасности сайтов. Цель и сущность, объекты охраны, методы и средства
Обеспечение безопасности сайтов. Цель и сущность, объекты охраны, методы и средства Беседа. Правила безопасности в интернете
Беседа. Правила безопасности в интернете Интернет как инструмент для общения. Интернет ресурсы как способ проповеди Евангелия
Интернет как инструмент для общения. Интернет ресурсы как способ проповеди Евангелия Операционные системы. Определение ОС
Операционные системы. Определение ОС Информационное обеспечение профессиональной деятельности. Конкурс электронных пособий
Информационное обеспечение профессиональной деятельности. Конкурс электронных пособий Автоматизированное рабочее место (АРМ) специалиста
Автоматизированное рабочее место (АРМ) специалиста Работа с дилерскими подсайтами
Работа с дилерскими подсайтами The Greetings Song
The Greetings Song HRM and its challenges
HRM and its challenges Концептуальное и даталогическое проектирование баз данных
Концептуальное и даталогическое проектирование баз данных Основные команды PLC
Основные команды PLC Двоичное кодирование
Двоичное кодирование УРВ решение для SMB ZKTime.net. Подключение Telegram к ZKTime.Net
УРВ решение для SMB ZKTime.net. Подключение Telegram к ZKTime.Net Технология обработки информации
Технология обработки информации Настойка ISO для фотокамер NIKON
Настойка ISO для фотокамер NIKON Юридическая компания Астрея. Кейс
Юридическая компания Астрея. Кейс Основы алгоритмизации
Основы алгоритмизации Интерфейс. Навигация и окна проекций. Autodesk 3ds max. Лекция №1
Интерфейс. Навигация и окна проекций. Autodesk 3ds max. Лекция №1 Обработка информации
Обработка информации Исполнитель Водолей
Исполнитель Водолей Лекция 2.3
Лекция 2.3 Введение в Data Science и Machine Learning
Введение в Data Science и Machine Learning 9-1_Компьютерные сети
9-1_Компьютерные сети