Система счисления. Вводный урок. 7 класс

Системы
счисления
Урок – объяснение нового материала
Цели и задачи урока:
актуализировать изученные ранее в курсе математики подходы к представлению числовой информации;
познакомить учащихся с понятиями ПОЗИЦИОННАЯ система счисления и НЕПОЗИЦИОННАЯ система счисления

Способ отображения чисел
(АЛФАВИТ)
Правила
действий
над ними
+
Системы
счисления

Способ отображения чисел
(АЛФАВИТ)
Правила
действий
над ними
+
Системы
счисления

АЛФАВИТ
любой системы счисления
формируется
из специальных символов -
ЦИФР
1
V
X
С
L
I
5
M
2
3
4
6
0
7
8
9
Системы
счисления

позиционные
непозиционные
значение цифры
НЕ ЗАВИСИТ
от ее позиции
в записи числа
значение цифры ЗАВИСИТ
от ее позиции в записи числа
3 303 0,33
V VII XIV
Системы
счисления

позиционные
непозиционные
значение цифры
НЕ ЗАВИСИТ
от ее позиции
в записи числа
значение цифры ЗАВИСИТ
от ее позиции в записи числа
3 303 0,33
V VII XIV
Системы
счисления

Непозиционная
Римская система счисления
I
V
l
C
X
D
M
один
пять
десять
пятьдесят
сто
пятьсот
тысяча
Числа формируются
с использованием
двух правил:
ПРАВИЛО
СЛОЖЕНИЯ
ПРАВИЛО
ВЫЧИТАНИЯ
Для записи чисел
используются буквы
ЛАТИНСКОГО алфавита:

Непозиционная
Римская система счисления
I
V
l
C
X
D
M
один
пять
десять
пятьдесят
сто
пятьсот
тысяча
Числа формируются
с использованием
двух правил:
ПРАВИЛО
СЛОЖЕНИЯ
ПРАВИЛО
ВЫЧИТАНИЯ
Для записи чисел
используются буквы
ЛАТИНСКОГО алфавита:

ПРАВИЛО СЛОЖЕНИЯ
Каждый меньший знак,
поставленный справа от большего,
прибавляется к нему.
X+I=XI
I < X
v+I=vI
v > I
10+1=11
5+1=6
5>1
1<10
=>
=>
XI
VI
11
6

ПРАВИЛО ВЫЧИТАНИЯ
каждый меньший знак,
поставленный слева от большего,
вычитается из него.
X-I=IX
I < X
v-I=Iv
v > I
10-1=9
5-1=4
5>1
1<10
=>
=>
IX
IV
9
4

НЕДОСТАТКИ
непозиционных систем счисления
НЕТ НУЛЯ;
НЕТ ДРОБНЫХ И ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ;
СЛОЖНО ВЫПОЛНЯТЬ АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ;
ДЛЯ ЗАПИСИ БОЛЬШИХ ЧИСЕЛ ПРИХОДИТСЯ ВВОДИТЬ ДОПОЛНИТЕЛЬНЫЕ СИМВОЛЫ (ЦИФРЫ).

Переведите числа в привычную нам
систему счисления
XIX
VIII
CCC
CxCVIII
lXiV
Cm
19
8
300
198
64
900

ОСНОВНЫЕ ДОСТОИНСТВА
позиционных систем счисления
ПРОСТОТА ВЫПОЛНЕНИЯ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ;
ОГРАНИЧЕННОЕ КОЛИЧЕСТВО СИМОЛОВ (ЦИФР), ИСПОЛЬЗУЕМЫХ ДЛЯ ЗАПИСИ ЧИСЕЛ.

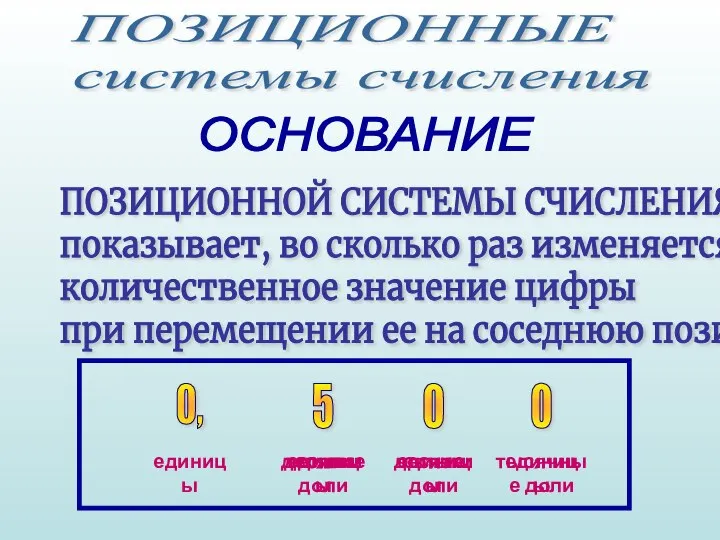
ПОЗИЦИОННОЙ СИСТЕМЫ СЧИСЛЕНИЯ
показывает, во сколько раз изменяется
количественное значение цифры
при перемещении ее на соседнюю позицию.
ОСНОВАНИЕ
5
единицы
0
единицы
десятки
0,
единицы
десятые
доли
0
единицы
десятки
сотни
сотые доли
тысячные доли
ПОЗИЦИОННЫЕ
системы счисления

В системе счисления с основанием q
(q-ичная система счисления)
Например,
если q=6, то в алфавите системы будут цифры:
0, 1, 2, 3, 4, 5 (всего 6 цифр),
а система счисления будет называться ШЕСТИРИЧНОЙ

Возможно множество позиционных систем, так как за основание системы счисления принимается любое число не меньшее 2.
основание позиционной системы счисления
также показывает количество цифр,
используемых для изображения
чисел в данной системе счисления.
десятичная,
двоичная,
восьмеричная, и т.д.
Наименование системы счисления соответствует ее основанию:

Это система счисления с основанием 10 (q=10),
в которой для записи чисел используются цифры
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
ДЕСЯТИЧНАЯ
позиционная система счисления
Десятичная система характеризуется тем, что в ней 10 единиц какого-либо разряда образуют единицу следующего старшего разряда.
1+ 1+ 1+ 1+ 1+ 1+ 1+ 1+ 1= 9
10
десятки
единицы
+ 1

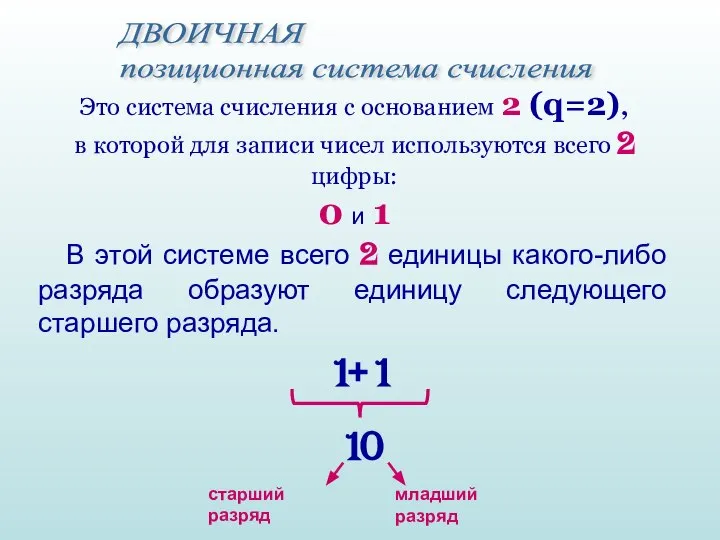
ДВОИЧНАЯ
позиционная система счисления
Это система счисления с основанием 2 (q=2),
в которой для записи чисел используются всего 2 цифры:
0 и 1
В этой системе всего 2 единицы какого-либо разряда образуют единицу следующего старшего разряда.
1+ 1
10
старший разряд
младший разряд