Система вибору та візуалізації найкоротшого маршруту при переміщенні об’єкта у приміщенні

Актуальнicть роботи
Безліч завдань оптимізації пов'язана саме з пошуком найкоротших шляхів.
Алгоритми пошуку найкоротших шляхів поділяються на два типи: пошук шляху на дискретному робочому полі (лабіринті), пошук шляху на графі. Обидва класи алгоритмів мають свої переваги і недоліки, а так само свою вузьку сферу застосування.
З розвитком робототехніки актуальним завданням є оптимальне переміщення автономного мобільного робота в приміщенні.

Об'єкт та предмет дослідження
Предметом дослідження магістерської роботи є моделі та алгоритми пошуку найкоротшого шляху між заданими точками, при переміщенні об’єкта (робота) в приміщенні.
Об'єктом дослідження є управління автономним об’єктом (роботом).

Мета і завдання дослідження
Для досягнення мети в магістерській роботі поставлені і вирішені наступні завдання:
провести аналіз існуючих алгоритмів пошуку короткого шляху (ланцюгу) між двома точками, у якому мінімізується сума всіх переміщень, що утворюють шлях;
розробити інформаційну технологію, представлену у вигляді моделюючого середовища побудови приміщення та пошуку найкоротшого маршруту між двома точками (стартової та фінішної) за допомогою трьох обраних алгоритмів;
провести експерименти побудови маршруту для конкретних вихідних даних та оцінити роботу відповідних алгоритмів.

Практичне значення отриманих результатів
Практичне значення отриманих результатів дослідження полягає в наступному:
Було проведено тестування розроблених алгоритмів та порівняння отриманих результатів формування оптимального маршруту. Найкращим виявився алгоритм Contraction hierarchies, що показав стабільні результати по часу та по якості побудованих маршрутів, як на малих дистанціях, так і на великих дистанціях.
Результати наукових досліджень використані при побудові інформаційної технології, яка може бути інтегрована в систему управління автономним мобільним роботом, де необхідна наявність сучасного апарату вироблення ефективних управлінських рішень або використані при побудові інтелектуального об’єкту в комп’ютерній грі.

Аналіз методів вирішення проблеми
До найбільш популярних алгоритмів пошуку маршруту в графі можна віднести:
Алгоритм Дейкстри знаходить найкоротший шлях від однієї з вершин графа до всіх інших. Алгоритм працює тільки для графів без ребер з негативною вагою;
Алгоритм Беллмана-Форда знаходить найкоротші шляхи від однієї вершини графа до всіх інших у зваженому графі. Вага ребер може бути негативною;
Алгоритм пошуку A * знаходить маршрут з найменшою вартістю від однієї вершини (початкової) до іншої (цільової, кінцевої), використовуючи алгоритм пошуку по першому найкращому збігу на графі;
Алгоритм Флойда-Уоршелла знаходить найкоротші шляхи між усіма вершинами зваженого орієнтованого графа;

Алгоритм Джонсона знаходить найкоротші шляхи між усіма парами вершин зваженого орієнтованого графа;
Алгоритм Лі (хвильовий алгоритм) заснований на методі пошуку в ширину. Знаходить шлях між вершинами s і t графа (s не збігається з t), що містить мінімальну кількість проміжних вершин (ребер). Основне застосування - трасування електричних з'єднань на кристалах мікросхем і на друкованих платах. Так само використовується для пошуку найкоротшої відстані на карті в стратегічних іграх;
Contraction hierarchies. Алгоритм з передбробкою графу для знаходження коротших шляхів і «віртуального» видалення вершин які можна пропустити при пошуку маршруту.

Математична модель
Задача про найкоротший шлях полягає в знаходженні найкоротшого шляху від заданої початкової вершини до заданої вершини.
Нехай – зважений орієнтований граф з матрицею ваг дуг ,
якщо .
Якщо в графі є деякий шлях, який послідовно проходить через вершини
то його вагою є величина :

Нехай u — вершина, від якої шукаються відстані, V — множина вершин графа, di — відстань від вершини u до вершини i, , w(i, j) — вага «ребра» (i, j).
Алгоритм:
1. Множина вершин U, до яких відстань відома, встановлюється рівною {u}.
2. Якщо U=V, алгоритм завершено.
3. Потенційні відстані Di до вершин з V\U встановлюються нескінченними.
4. Для всіх ребер (i, j), де i∈U та j∈V\U, якщо Dj>di+w(i, j), то Dj присвоюється di+w(i, j).
5. Шукається i∈V\U, при якому Di мінімальне.
6. Якщо Di дорівнює нескінченності, алгоритм завершено. В іншому випадку di присвоюється значення Di, U присвоюється U∪{i} і виконується перехід до кроку 2.
Алгоритм Дейкстри

Алгоритм Contraction Hierarhies
Підхід скорочення ієрархій (Contraction Hierarchies) полягає у використанні концепції міток (shortcuts або «скорочуючих ребер») - найкоротших шляхів. Мітка найкоротшого шляху – це дуга (u, v), яка не обов’язково існує у початковому графі, але позначає найкоротший шлях з u до v в графі G.

Проектна модель
Моделювання будь-якої системи супроводжується створенням множини моделей для відображення різних аспектів системи. Моделі можуть мати різні рівні абстракції, які відображають одні й ті ж аспекти системи з різним ступенем деталізації.

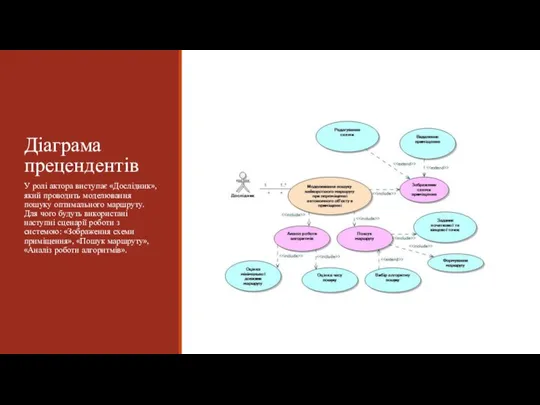
Діаграма прецендентів
У ролі актора виступає «Дослідник», який проводить моделювання пошуку оптимального маршруту. Для чого будуть використані наступні сценарії роботи з системою: «Зображення схеми приміщення», «Пошук маршруту», «Аналіз роботи алгоритмів».

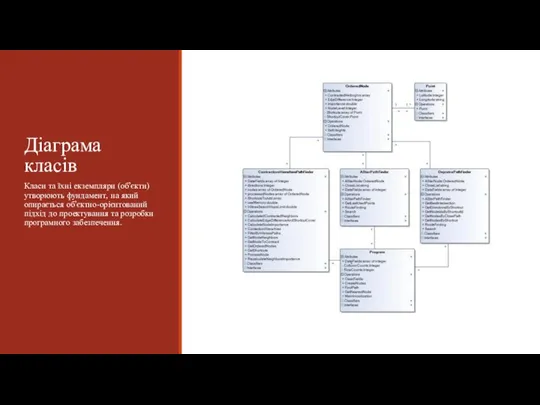
Діаграма класів
Класи та їхні екземпляри (об’єкти) утворюють фундамент, на який опирається об’єктно-орієнтований підхід до проектування та розробки програмного забезпечення.

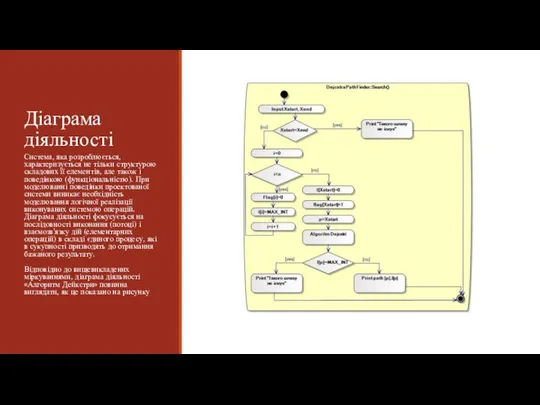
Діаграма діяльності
Система, яка розроблюється, характеризується не тільки структурою складових її елементів, але також і поведінкою (функціональністю). При моделюванні поведінки проектованої системи виникає необхідність моделювання логічної реалізації виконуваних системою операцій. Діаграма діяльності фокусується на послідовності виконання (потоці) і взаємозв'язку дій (елементарних операцій) в складі єдиного процесу, які в сукупності призводять до отримання бажаного результату.
Відповідно до вищевикладених міркуваннями, діаграма діяльності «Алгоритм Дейкстри» повинна виглядати, як це показано на рисунку

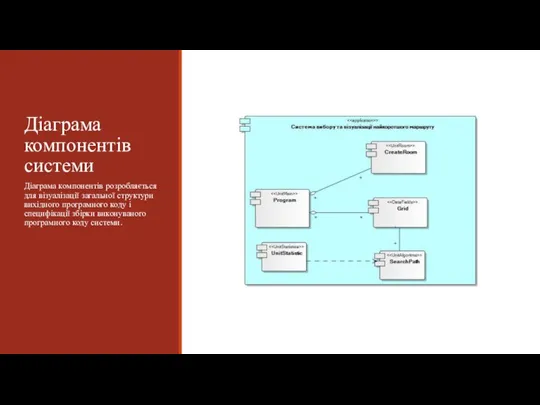
Діаграма компонентів системи
Діаграма компонентів розробляється для візуалізації загальної структури вихідного програмного коду і специфікації збірки виконуваного програмного коду системи.

Інформаційне забезпечення
Програмний продукт реалізовано на платформі .Net, мові програмування С# та технології WPF. В якості СУБД використовується Microsoft SQL Server. Реалізовані алгоритми можуть використовуватись в якості графічної оболонки для візуалізації роботи та для тестування.
Запорукою успішного проектування і реалізації системи вибору та візуалізації найкоротшого маршруту при переміщенні об’єкта у приміщенні є побудова адекватної, повної і несуперечливої інформаційної моделі.

Сутність дослідження
Дослідження полягало в порівнянні алгоритмів Дейкстри, А* і Contraction hierarchies для невеликого приміщення. Для порівняння роботи алгоритмів пошуку запускали процедури пошуку на різних маршрутах. Причому маршрути в вибірці були як короткі так і довгі, оскільки реалізовані алгоритми по-різному показали себе на маршрутах різної довжини.

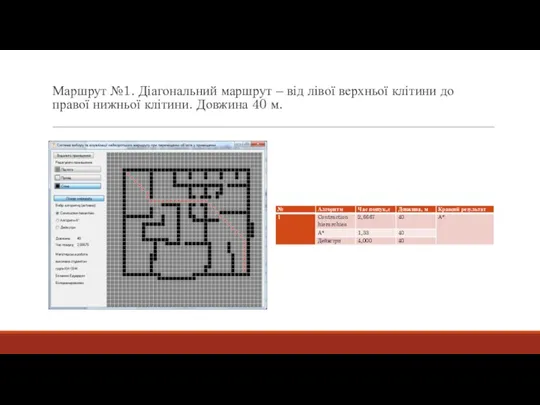
Маршрут №1. Діагональний маршрут – від лівої верхньої клітини до правої нижньої клітини. Довжина 40 м.

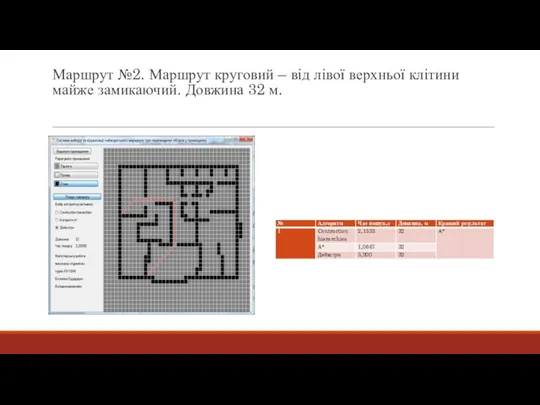
Маршрут №2. Маршрут круговий – від лівої верхньої клітини майже замикаючий. Довжина 32 м.

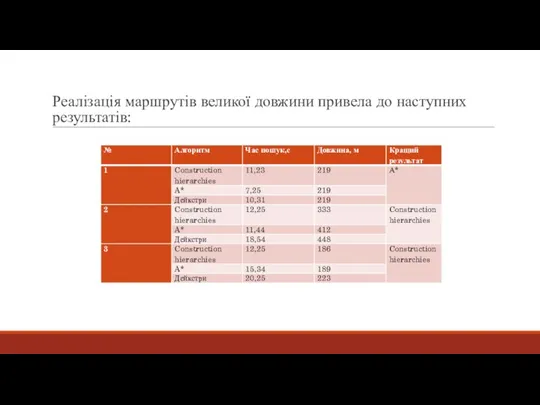
Реалізація маршрутів великої довжини привела до наступних результатів:

Висновки
Поставлена мета дослідження досягнута. Розроблені моделі пошуку найкоротшого маршруту при пересуванні об’єкту в приміщенні, спрямовані на вдосконалення відомих підходів (Дейкстри, Алгоритм А*, Contraction hierarchies) та вибраний оптимальний алгоритм.
Для досягнення мети в магістерській роботі поставлені і вирішені наступні завдання:
проведено аналіз існуючих алгоритмів пошуку короткого шляху (ланцюгу) між двома точками, у якому мінімізується сума всіх переміщень, що утворюють шлях;
розроблено інформаційну технологію, представлену у вигляді моделюючого середовища побудови приміщення та пошуку найкоротшого маршруту між двома точками (стартовой та фінішной) за допомогою трьох обраних алгоритмів;
проведені експерименти побудови маршруту для конкретних вихідних даних та проведено оцінку роботи відповідних алгоритмів.