Слайд 2Содержание
Необыкновенная девочка
Понятие и история развития систем счисления
Позиционные и непозиционные системы счисления
22,

82, 8, 16 системы счисления
Перевод чисел в 2, 8, 16 системы счисления
Перевод чисел из 2, 8, 16 системы счисления в десятичную
Правила преобразования
Тест
Контрольная работа
Слайд 3Необыкновенная девочка
Ей было 1100 лет
Она в 101 класс ходила
В портфеле по 100

книг носила
Всё это правда,
А не бред
Когда пыля 10 ног,
Она бежала по дороге
За ней всегда бежал щенок
С одним хвостом
Зато 100 – ногий.
И 10 удивлённых глаз
Смотрели в этот мир привычно
Но станет всё совсем обычно
Когда поймете наш рассказ!
Слайд 4 Система счисления – это знаковая система, в которой числа записываются по

определенным правилам с помощью символов некоторого алфавита, которые называют цифрами.
Слайд 5История развития систем счисления
У первобытных народов не существовало развитой системы счисления. Ещё

в 19 в. у многих племён Австралии и Полинезии было только два числительных: один и два; сочетания их образовывали числа: 3 — два-один, 4 — два-два, 5 — два-два-один и 6 — два-два-два. О всех числах, больших 6, говорили: “много”, не индивидуализируя их.
Слайд 6 Египтяне впервые ввели десятичную систему счисления, правда без позиционного обозначения. В

развитии математики в государствах ислама получила распространение десятичная позиционная система счисления с применением нуля, ведущая своё происхождение от индийской математики. Возникновение десятичной системы счисления связано со счётом на пальцах. Имелись системы счисления и с другим основанием: 5, 12 (счёт дюжинами), 20 (следы такой системы сохранились во французском языке, например quatre-vingts, то есть буквально четыре-двадцать, означает 80, 40, 60 и др.
Слайд 7 Вавилонские математики широко пользовались созданной ещё шумерами шестидесятеричной позиционной системой счёта;

на основе этой системы были составлены различные вычислительные таблицы: деления и умножения чисел, квадратов и кубов чисел и их корней (квадратных и кубических).
Слайд 8Перевод чисел в 2, 8, 16 системы счисления
При переводе чисел из

десятичной системы счисления в систему с основанием P > 1 обычно используют следующий алгоритм:
1) если переводится целая часть числа, то она делится на P, после чего запоминается остаток от деления. Полученное частное вновь делится на P, остаток запоминается. Процедура продолжается до тех пор, пока частное не станет равным нулю. Остатки от деления на P выписываются в порядке, обратном их получению;
2) если переводится дробная часть числа, то она умножается на P, после чего целая часть запоминается и отбрасывается. Вновь полученная дробная часть умножается на P и т.д. Процедура продолжается до тех пор, пока дробная часть не станет равной нулю.
Целые части выписываются после двоичной запятой в порядке их получения. Результатом может быть либо конечная, либо периодическая двоичная дробь. Поэтому, когда дробь является периодической, приходится обрывать умножение на каком-либо шаге и довольствоваться приближенной записью исходного числа в системе с основанием P.
Перевод чисел из 2, 8, 16 системы счисления.
При переводе чисел из системы счисления с основанием P в десятичную систему счисления необходимо пронумеровать разряды целой части справа налево, начиная с нулевого, и дробной части, начиная с разряда сразу после запятой, слева направо (начальный номер –1). Затем вычислить сумму произведений соответствующих значений разрядов на основание системы счисления в степени, равной номеру разряда. Это и есть представление исходного числа в десятичной системе счисления
Слайд 9 В непозиционных системах счисления значение (величина) числа определяется как сумма или

разность цифр в числе.
Недостатки непозиционных систем счисления
Существует постоянная потребность введения новых знаков для записи больших чисел.
Невозможно представлять дробные и отрицательные числа.
Сложно выполнять арифметические операции, т.к. не существует алгоритмов их выполнения
Слайд 10В позиционных системах счисления значение цифры зависит от ее места (позиции) в

числе, а в непозиционных не зависит.
В позиционной системе счисления один и тот же числовой символ приобретает различные значения (имеет различный вес) в зависимости от позиции.
Каждая позиция соответствует определенной степени основания системы счисления. Основание равно количеству цифр (знаков в алфавите системы счисления) и определяет, во сколько раз отличаются значения одинаковых цифр, стоящих в соседних позициях
Достоинства позиционных систем счисления
Простота выполнения арифметических операций.
Ограниченное количество символов (цифр) для записи любых чисел









 Minecraft
Minecraft Интернет в моей жизни
Интернет в моей жизни Классификация ИС
Классификация ИС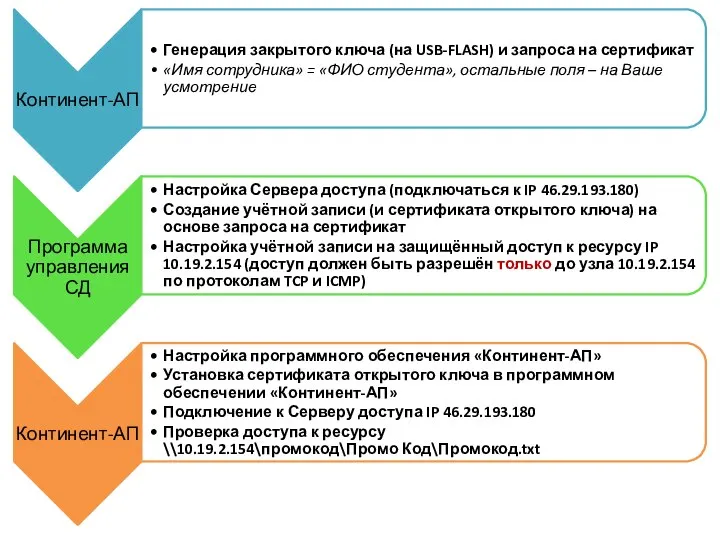 Континент-АП. Программа управления СД TCP и ICMP
Континент-АП. Программа управления СД TCP и ICMP Сообщество Детский нейропсихолог. Нейрокоррекция
Сообщество Детский нейропсихолог. Нейрокоррекция Упаковка и распаковка данных с помощью программ-архиваторов. WinRAR
Упаковка и распаковка данных с помощью программ-архиваторов. WinRAR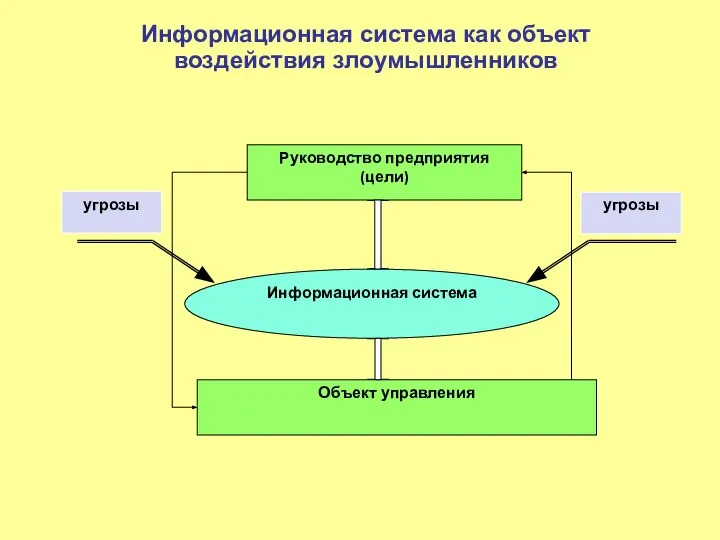 Информационная система как объект воздействия злоумышленников
Информационная система как объект воздействия злоумышленников Тайны кроссворда
Тайны кроссворда Занятие № 2 Основы программирования на C#
Занятие № 2 Основы программирования на C# Эквивалентные состояния и эквивалентные автоматы. Задача минимизации автоматов
Эквивалентные состояния и эквивалентные автоматы. Задача минимизации автоматов Схемы программ
Схемы программ Иерархические, сетевые и реляционные БД
Иерархические, сетевые и реляционные БД Времена года - зима
Времена года - зима Электронная почта
Электронная почта Не дай себя обмануть!
Не дай себя обмануть! Системное моделирование
Системное моделирование Основы разработки экспертных систем
Основы разработки экспертных систем Блоги и блогеры
Блоги и блогеры Специфіка відтворення академічної термінології при перекладі й локалізації вебсайтів
Специфіка відтворення академічної термінології при перекладі й локалізації вебсайтів Работай, хватит в фейсбуке сидеть! или как построить личный бренд
Работай, хватит в фейсбуке сидеть! или как построить личный бренд Циклический алгоритм
Циклический алгоритм Golem Forge
Golem Forge Формирование вероятностно-статистических моделей объектов эксплуатации летательных аппаратов
Формирование вероятностно-статистических моделей объектов эксплуатации летательных аппаратов Принципы построения и функционирования компьютерных сетей. Службы сети Интернет, коммерция и право
Принципы построения и функционирования компьютерных сетей. Службы сети Интернет, коммерция и право Метрология и теория измерений
Метрология и теория измерений Okna_i_operatsii_nad_oknami
Okna_i_operatsii_nad_oknami Исполнители вокруг нас
Исполнители вокруг нас Введите название презентации
Введите название презентации