Формирование вероятностно-статистических моделей объектов эксплуатации летательных аппаратов

Исходные данные и порядок формирования
вер.-стат. модели эксплуатации
Исходными данными для формирования вер.-стат. модели являются экспериментальные результаты исследований параметров компонент эксплуатации.
На основании исходных данных строится гистограмма распределений (плотности распределения или частости). По виду этой гистограммы выдвигается гипотеза о виде закона распределения исследуемого параметра. Эта гипотеза проверяется с помощью критерия согласия. При подтверждении гипотезы она принимается, а в случае отказа в подтверждении гипотезы - корректируется вер.-стат. модель.

Законы распределения непрерывных случайных величин, используемые при формировании вер.-стат. моделей
В практике эксплуатации АТ встречаются следующие непрерывные распределения вероятностей:
нормальное,
экспоненциальное,
Вейбулла,
гамма-распределение,
логарифмически-нормальное

Ход работы
Получить исходные данные. Исходным материалом являются статистические данные, вариационный ряд - набор чисел в порядке возрастания
Выбрать математическую модель, которая наиболее полно соответствует вариационному ряду. Модель соответствует одному из распределения непрерывных случайных величин: нормальный, экспоненциальный или Вейбулла.

Пример
Таблица исходных данных:
1. Сгруппируем статистические данные (из таблицы своего варианта) в интервалы. Длины интервала определяется формуле (6.1.1).
N = 30 - общее число значений случайной величины (число значений в таблице)
Найдем границы всех интервалов:
1-ый интервал – от 70 до 70+464=534
2-ой интервал – от 534 до 534+464=998
3-ий интервал – от 998 до 1463
4-ый интервал – от 1463 до 1927
5-ый интервал – от 1927 до 2392
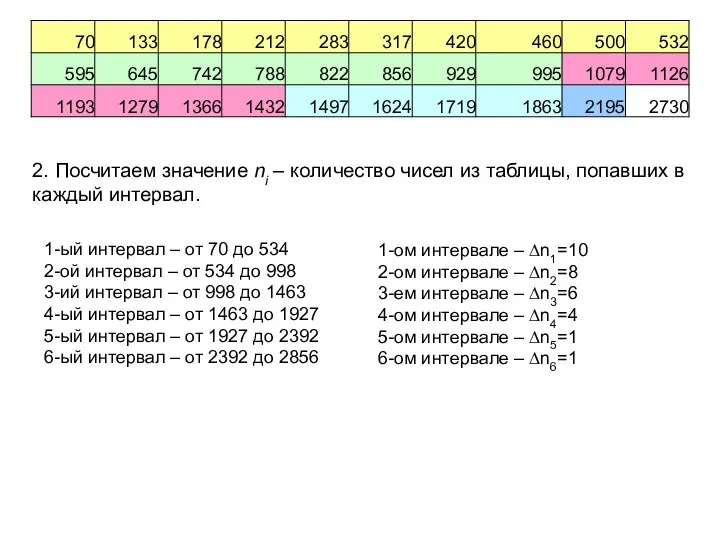
6-ый интервал – от 2392 до 2856

2. Посчитаем значение ni – количество чисел из таблицы, попавших в каждый интервал.
1-ом интервале – ∆n1=10
2-ом интервале – ∆n2=8
3-ем интервале – ∆n3=6
4-ом интервале – ∆n4=4
5-ом интервале – ∆n5=1
6-ом интервале – ∆n6=1
1-ый интервал – от 70 до 534
2-ой интервал – от 534 до 998
3-ий интервал – от 998 до 1463
4-ый интервал – от 1463 до 1927
5-ый интервал – от 1927 до 2392
6-ый интервал – от 2392 до 2856

1-ом интервале – ∆n1=10 f1=0,00071 P*1=0,3333
2-ом интервале – ∆n2=8 f2=0,00057 P*2=0,2666
3-ем интервале – ∆n3=6 f3=0,00043 P*3=0,2
4-ом интервале – ∆n4=4 f4=0,00028 P*4=0,1333
5-ом интервале – ∆n5=1 f5=0,000071 P*5=0,0333
6-ом интервале – ∆n6=1 f6=0,000071 P*6=0,0333
3. Значения статистической плотности распределения f*i в i-м интервале рассчитывается по формуле (6.1.2)
4. Значения частостей Pi* показывают вероятность нахождения случайной величины в каждом интервале (6.1.3).

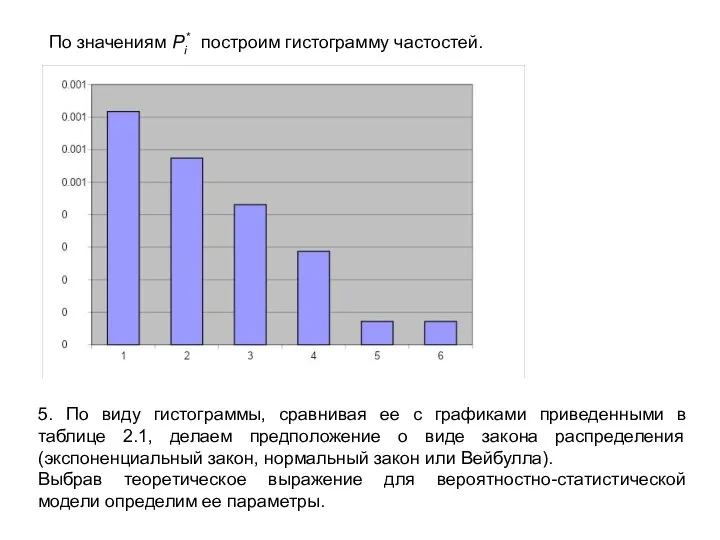
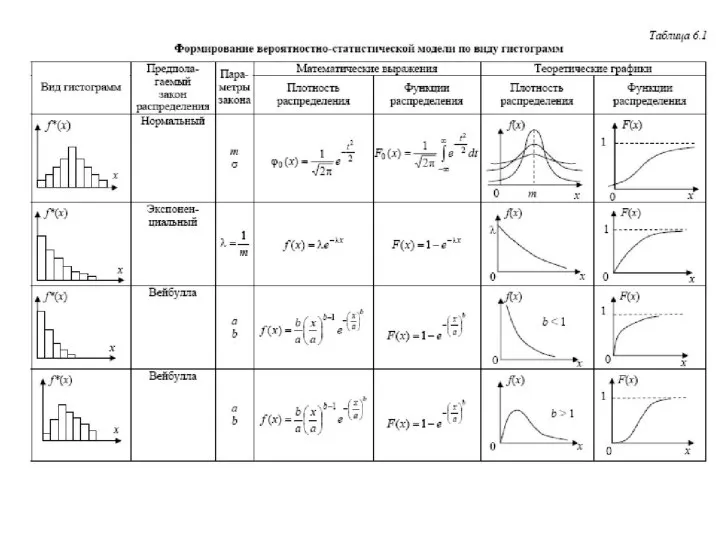
По значениям Pi* построим гистограмму частостей.
5. По виду гистограммы, сравнивая ее с графиками приведенными в таблице 2.1, делаем предположение о виде закона распределения (экспоненциальный закон, нормальный закон или Вейбулла).
Выбрав теоретическое выражение для вероятностно-статистической модели определим ее параметры.

6. Определим математическое ожидание m (6.1.4), дисперсию (6.1.5)
и среднеквадратическое отклонение σ (6.1.6).
Где Xi - расстояние от середины интервала до начала координат
X1=70+(464/2)=302 – расстояние от середины 1-го интервала до 0
Х2=534+(464/2)=766 - расстояние от середины 2-го интервала до 0
Х3=998+(464/2)=1231 - расстояние от середины 3-го интервала до 0
Х4=1463+(464/2)=1695 - расстояние от середины 4-го интервала до 0
Х5=1927+(464/2)=2160 - расстояние от середины 5-го интервала до 0
Х6=2392+(464/2)=2624 - расстояние от середины 6-го интервала до 0

7. Определить параметры модели:
а) Экспоненциальный закон распределения - один параметр λ
б) Нормальный закон распределения - два параметра: математическое ожидание m (6.1.5) и среднеквадратическое отклонение σ (6.1.6)
в) Распределение Вейбулла – два параметра: величины а и b (6.1.9, 6.1.10 и табл 6.1.1)
или
ν - коэффициент вариации = 0,65
Kb=0,897
Cb=0,574
b=1,6 a=1044

Окончательное выражение
а) Экспоненциальный закон распределения
б) Нормальный закон распределения
в) Распределение Вейбулла

Лабораторная работа №2
Проверка соответствия выбранной модели экспериментальным данным с помощью критериев согласия
Проверяем соответствие выбранной модели экспериментальным данным.
1. Рассчитываем критерий Пирсона (критерий χ2расч.)по формуле (6.2.1) и сравниваем с значением χ2табл. (таблица 6.2.2).

k, Δni ,N рассчитаны ранее;
Pi – вероятность попадания случайной величины в i-й интервал в соответствии с теоретическим значением закона распределения выбранной модели (не путать со значением P*i из предыдущей лабораторной работы).

а) Величина Pi при экспоненциальном распределении – формула (6.2.4)
P1=e-λX0- e-λX1= e -λ*70 - e -λ*534
P2=e-λX1- e-λX2= e -λ*534 - e -λ*998
P3=e-λX2- e-λX3= e -λ*998 - e -λ*1463
P4=e-λX3- e-λX4= e -λ*1463 - e -λ*1927
P5=e-λX4- e-λX5= e -λ*1927 - e -λ*2392
P6=e-λX5- e-λX6= e -λ*2392 - e -λ*2856
Xi и Xi+1 - нижняя и верхняя границы интервала разбиения (Л.Р. №1)

б) Нормальное распределение – формула (6.2.2), величины F(xi+1) и F(xi) определяются с помощью таблицы (таблица 6.2.1). Вход в таблицу производится по значению величины
Если x<, то S<0 и F(–x)=1–F(x), если S>0, то берется непосредственно табличное значение.
Xi и Xi+1 - нижняя и верхняя границы интервала разбиения (Л.Р. №1)

в) Распределение Вейбула – формула (6.2.7) – в учебнике в формуле ошибка!
2. Затем по таблице 6.2.2 необходимо определить значение число степеней свободы r рассчитываем как r=k–1–l.
а) Для экспоненциального закона распределения l = 1
б) Для нормального закона l = 2,
в) Для закона Вейбула l = 2
γ >0,7 Чем больше γ, тем лучше соответствует выбранная модель экспериментальным данным.
Xi и Xi+1 - нижняя и верхняя границы интервала разбиения (Л.Р. №1)