Содержание
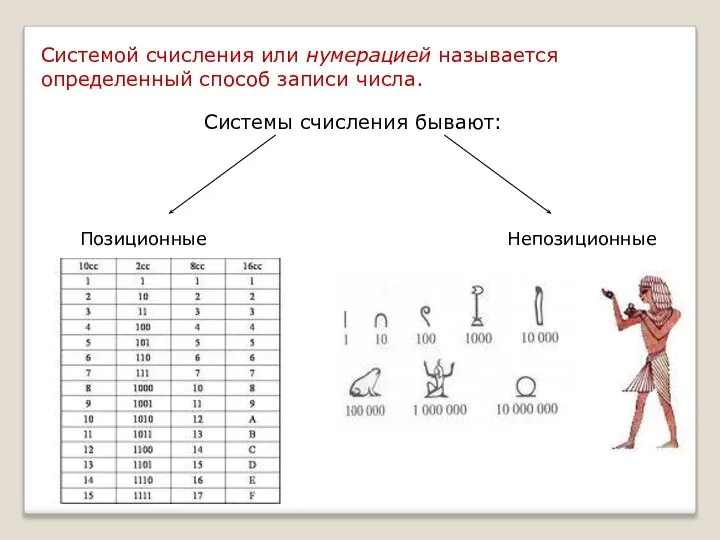
- 2. Системой счисления или нумерацией называется определенный способ записи числа. Системы счисления бывают: Позиционные Непозиционные
- 3. Основные понятия позиционных систем счисления Цифра – символ, используемый для записи числа. Алфавит – совокупность всех
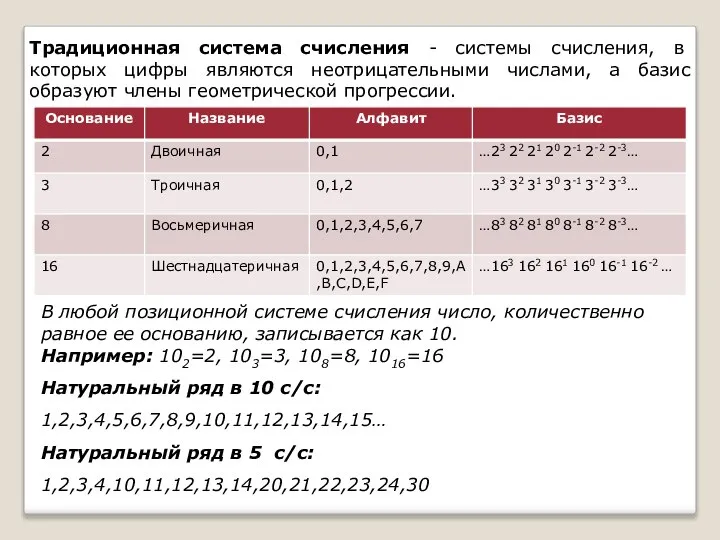
- 4. Традиционная система счисления - системы счисления, в которых цифры являются неотрицательными числами, а базис образуют члены
- 5. В позиционных системах счисления основание системы определяет, во сколько раз различаются значения различных разрядов. Например: При
- 6. Перевод чисел с применением схемы Горнера Перевод на примере целого восьмеричного числа 2317458 . Запишем число
- 7. Нетрадиционные системы счисления. Фибоначчиева система счисления. Базисом фибоначчиевой системы является последовательность 1, 2, 3, 5, 8,
- 8. Задание для самостоятельной работы: Задание 1 Запишите десятичные числа 30, 125 и 1949 в фибоначчиевой системе
- 9. Алгоритм перевода целых чисел из фибоначчиевой системы счисления в десятичную. В ФСС “вес” каждого разряда числа
- 10. В любой системе счисления 100 - минимальное трехзначное число. Поэтому ему предшествует максимальное двухзначное число, которое
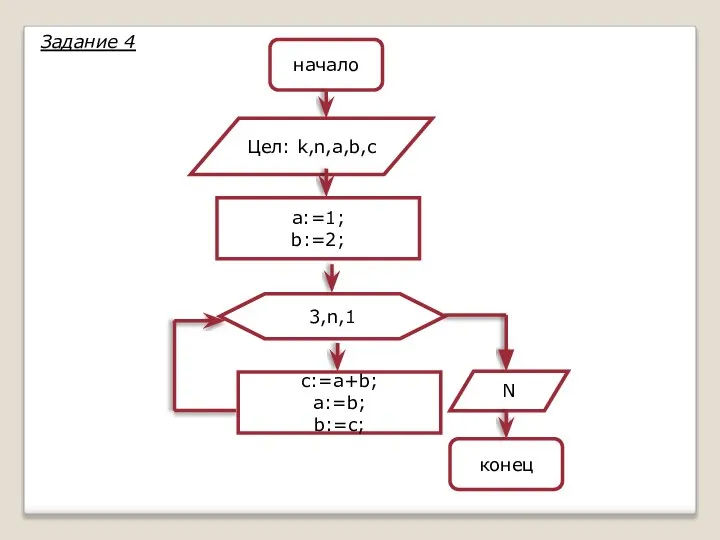
- 11. 3,n,1 начало Цел: k,n,a,b,c a:=1; b:=2; c:=a+b; a:=b; b:=c; N конец Задание 4
- 13. Скачать презентацию







 Webcard для детей
Webcard для детей Инфоратика. Склеивание мешков цепочек. 3 урок
Инфоратика. Склеивание мешков цепочек. 3 урок Графические редакторы
Графические редакторы Беспроводная сеть сбора метрологических данных
Беспроводная сеть сбора метрологических данных Эволюция и общие принципы построения сетей
Эволюция и общие принципы построения сетей Лаборатория интеллектуальных систем
Лаборатория интеллектуальных систем Аудит Рекламной Кампании
Аудит Рекламной Кампании Стенд по изучению азбуки Морзе
Стенд по изучению азбуки Морзе Объектная модель Excel
Объектная модель Excel Introduction to Database storage
Introduction to Database storage Презентация на тему Исследование биологической модели
Презентация на тему Исследование биологической модели  Общие сведения о языке программирования Паскаль. Начала программирования. Ключевые слова
Общие сведения о языке программирования Паскаль. Начала программирования. Ключевые слова ИТ-марафон
ИТ-марафон ТЗ на создание сайта СМ
ТЗ на создание сайта СМ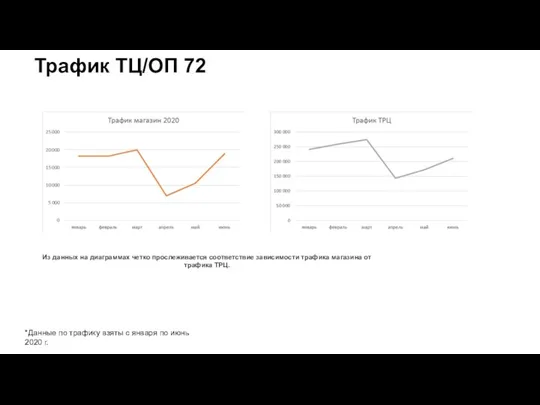 Трафик ТЦ/ОП 72
Трафик ТЦ/ОП 72 Таргетированная реклама
Таргетированная реклама Ввод информации в память компьютера. Урок 3
Ввод информации в память компьютера. Урок 3 Пред-лейнинг. Работа на лайнах
Пред-лейнинг. Работа на лайнах Вводная информация по работе с сервисным порталом TPV
Вводная информация по работе с сервисным порталом TPV Что мы знаем о компьютере?
Что мы знаем о компьютере? Вещественные числа
Вещественные числа Типы планирования. Алгоритмы планирования. Примеры реализации алгоритмов планирования в современных операционных системах
Типы планирования. Алгоритмы планирования. Примеры реализации алгоритмов планирования в современных операционных системах Основы HTML. Разработка Web-сайта
Основы HTML. Разработка Web-сайта Программирование в среде Robot C. Команды рисования
Программирование в среде Robot C. Команды рисования Как выбрать книгу
Как выбрать книгу SQLXML. Синтаксис XMLFOREST
SQLXML. Синтаксис XMLFOREST Коды. 8-11 класс
Коды. 8-11 класс Табличный процессор Microsoft Excel
Табличный процессор Microsoft Excel