Содержание
- 2. Системы счисления © К.Ю. Поляков, 2007-2012 Тема 1. Введение
- 3. Определения Система счисления – это способ записи чисел с помощью специальных знаков – цифр. Числа: 123,
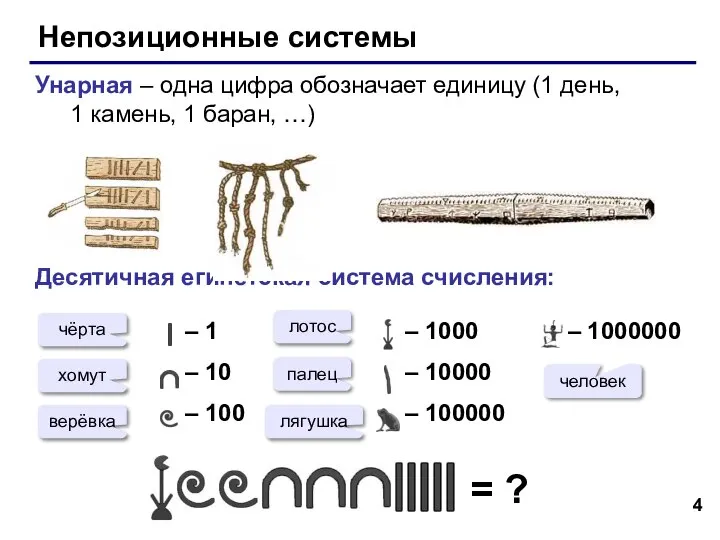
- 4. Непозиционные системы Унарная – одна цифра обозначает единицу (1 день, 1 камень, 1 баран, …) Десятичная
- 5. Непозиционные системы Римская система счисления: I – 1 (палец), V – 5 (раскрытая ладонь, 5 пальцев),
- 6. Римская система счисления Правила: (обычно) не ставят больше трех одинаковых цифр подряд если младшая цифра (только
- 7. Примеры: 3768 = 2983 = 1452 = 1999 =
- 8. Римская система счисления Недостатки: для записи больших чисел (>3999) надо вводить новые знаки-цифры (V, X, L,
- 9. Славянская система счисления алфавитная система счисления (непозиционная) Часы Суздальского Кремля
- 10. Позиционные системы Позиционная система: значение цифры определяется ее позицией в записи числа. Десятичная система: первоначально –
- 11. Позиционные системы Задача: в какой системе счисления число 58 записывается как «46x»? Определите основание системы счисления
- 12. Позиционные системы Задача: найдите основание системы счисления, в которой выполняется равенство в записи есть цифра 6,
- 13. Позиционные системы Задача: перечислите через запятую все системы счисления, в которых выполняется неравенство в записи есть
- 14. Позиционные системы Задача: найдите наименьшее основание системы счисления, в которой запись числа 30 имеет 3 значащих
- 15. Системы счисления © К.Ю. Поляков, 2007-2012 Тема 2. Двоичная система счисления
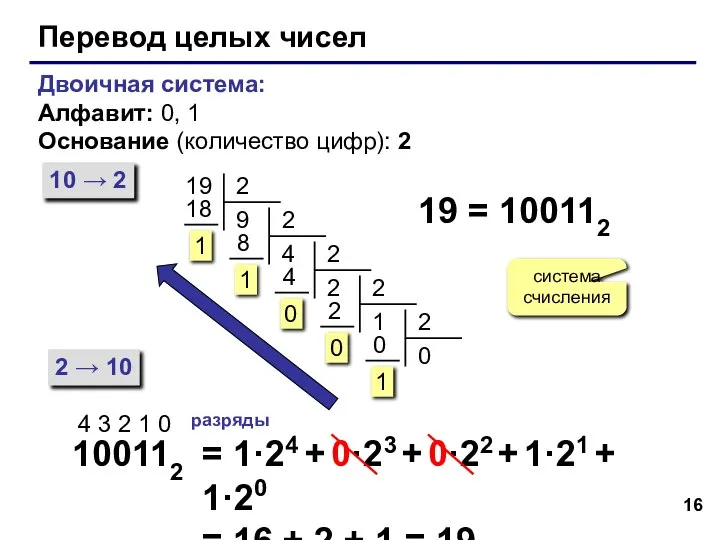
- 16. Перевод целых чисел Двоичная система: Алфавит: 0, 1 Основание (количество цифр): 2 10 → 2 2
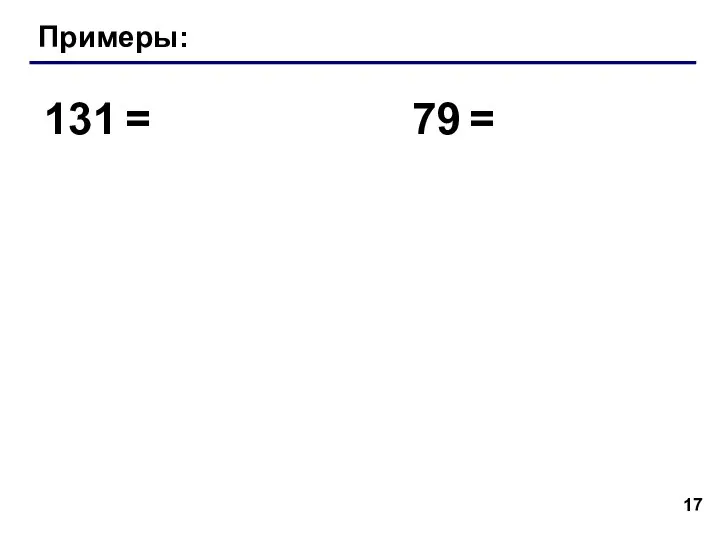
- 17. Примеры: 131 = 79 =
- 18. Примеры: 1010112 = 1101102 =
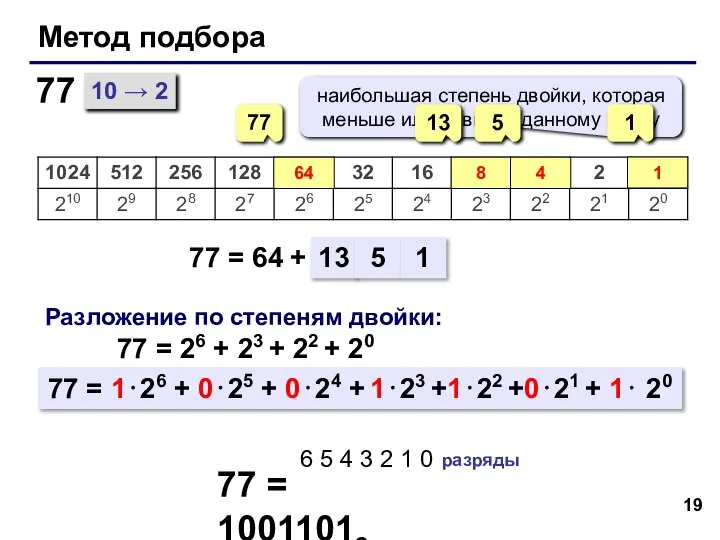
- 19. Метод подбора 10 → 2 77 = 64 + 77 77 64 Разложение по степеням двойки:
- 20. Перевод дробных чисел 10 → 2 2 → 10 0,375 = × 2 101,0112 2 1
- 21. Примеры: 0,625 = 3,875 =
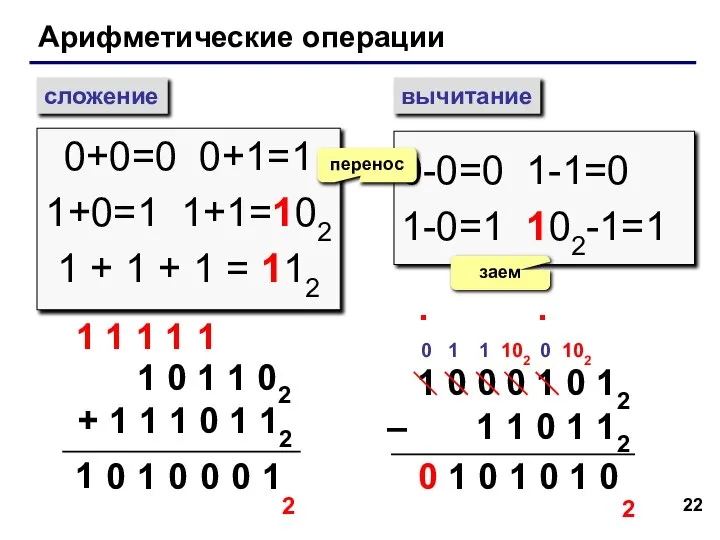
- 22. Арифметические операции сложение вычитание 0+0=0 0+1=1 1+0=1 1+1=102 1 + 1 + 1 = 112 0-0=0
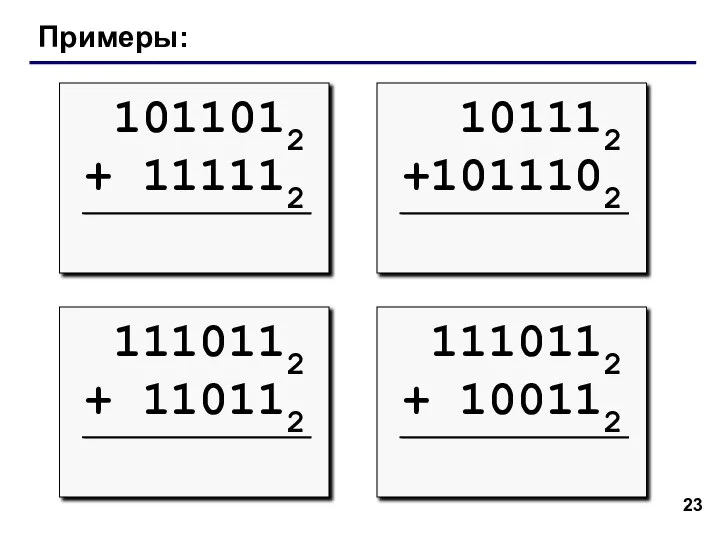
- 23. Примеры:
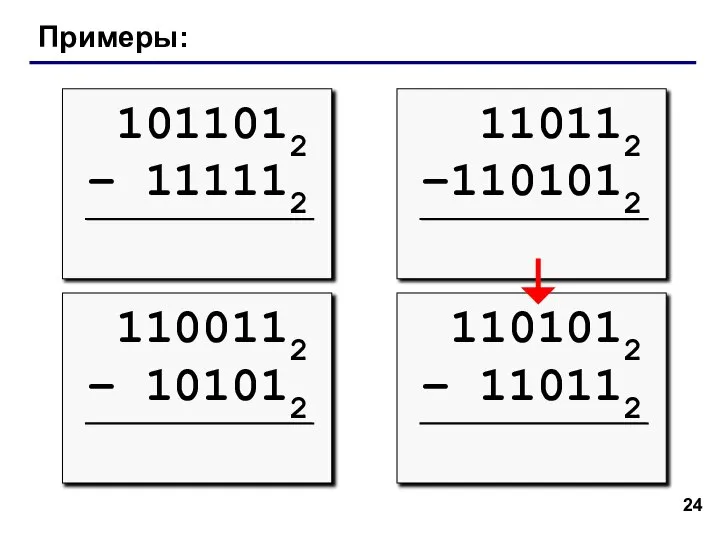
- 24. Примеры:
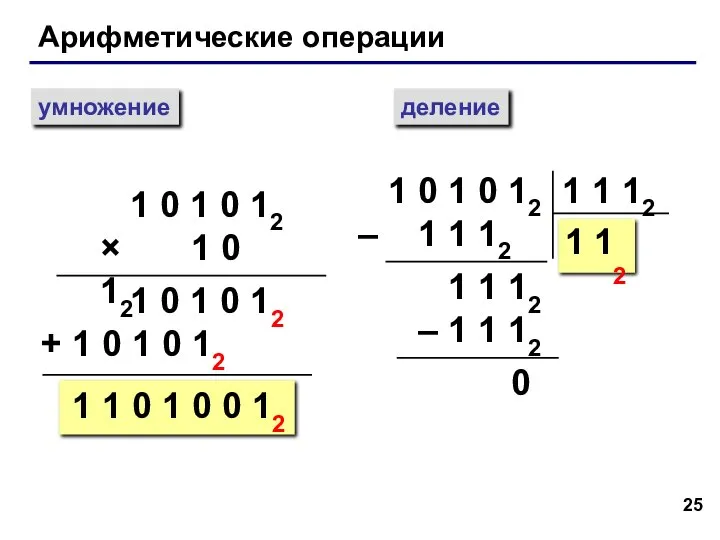
- 25. Арифметические операции умножение деление 1 0 1 0 12 × 1 0 12 1 0 1
- 26. Плюсы и минусы двоичной системы нужны устройства только с двумя устойчивыми состояниями (есть ток — нет
- 27. Двоично-десятичная система BCD = binary coded decimals (десятичные цифры в двоичном коде) 9024,19 = 1001 0000
- 28. Системы счисления © К.Ю. Поляков, 2007-2012 Тема 3. Восьмеричная система счисления
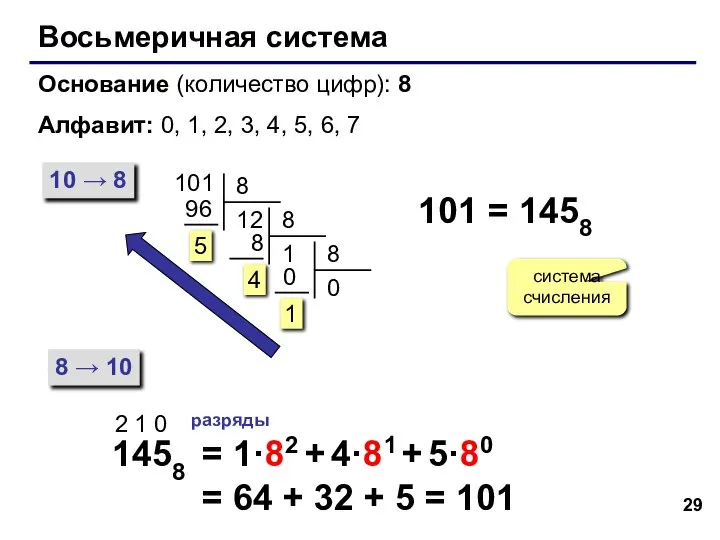
- 29. Восьмеричная система Основание (количество цифр): 8 Алфавит: 0, 1, 2, 3, 4, 5, 6, 7 10
- 30. Примеры: 134 = 75 = 1348 = 758 =
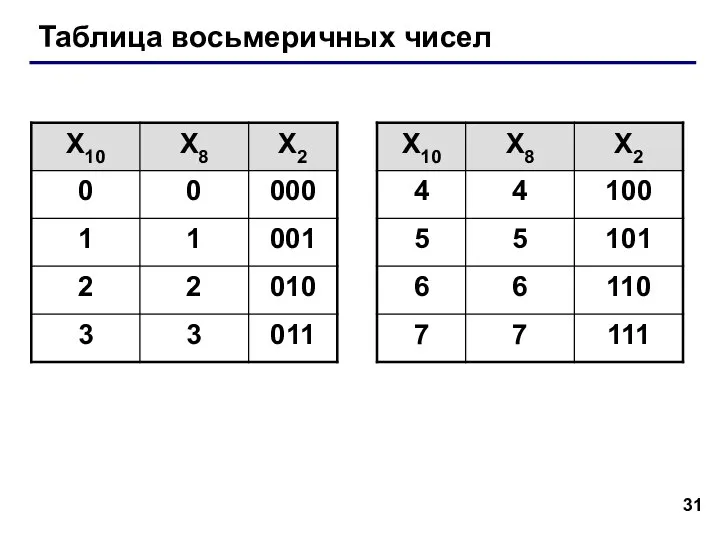
- 31. Таблица восьмеричных чисел
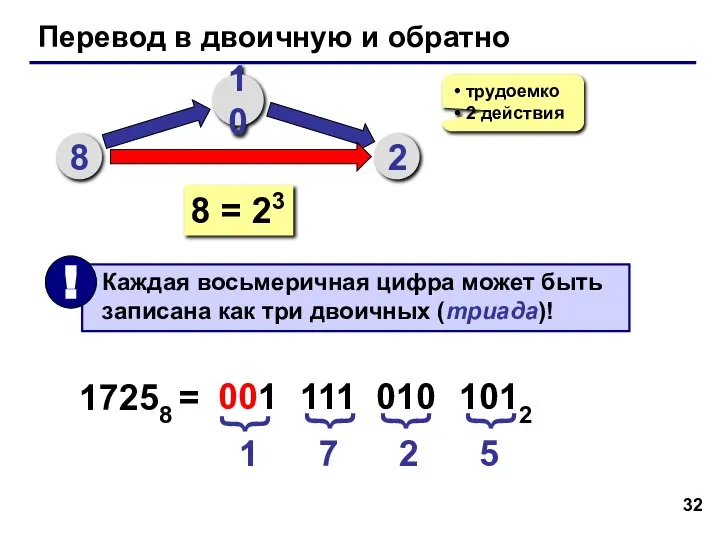
- 32. Перевод в двоичную и обратно 8 10 2 трудоемко 2 действия 8 = 23 17258 =
- 33. Примеры: 34678 = 21488 = 73528 = 12318 =
- 34. Перевод из двоичной системы 10010111011112 Шаг 1. Разбить на триады, начиная справа: 001 001 011 101
- 35. Примеры: 1011010100102 = 111111010112 = 11010110102 =
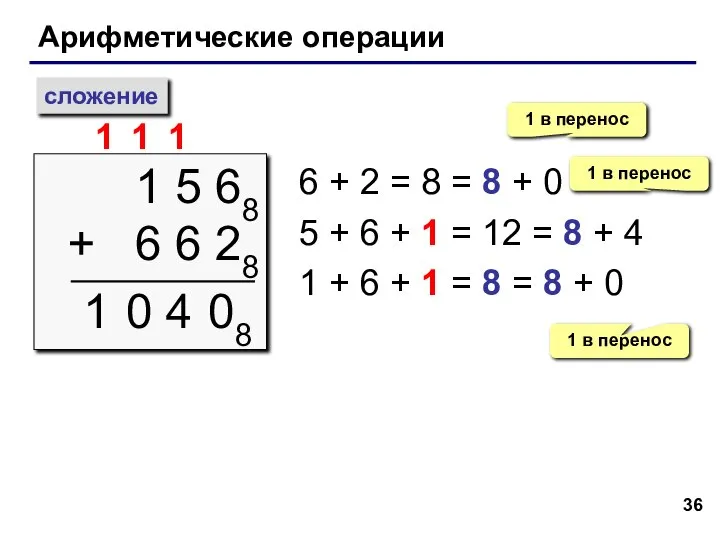
- 36. Арифметические операции сложение 1 5 68 + 6 6 28 1 1 6 + 2 =
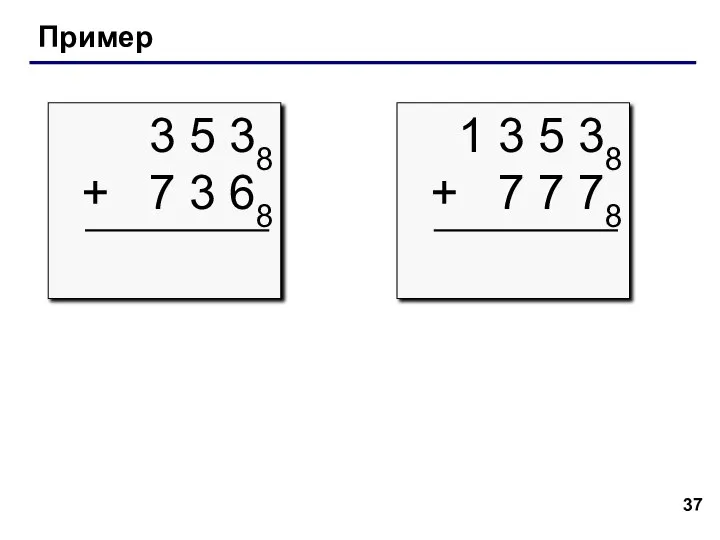
- 37. Пример
- 38. Арифметические операции вычитание 4 5 68 – 2 7 78 ∙ (6 + 8) – 7
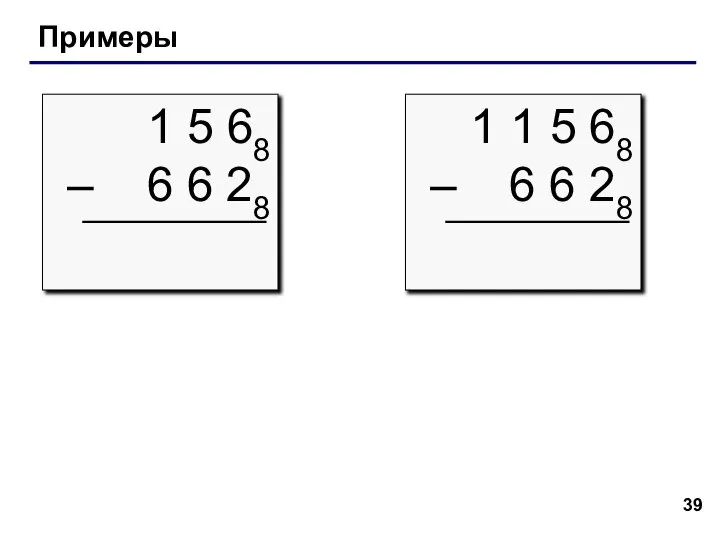
- 39. Примеры
- 40. Системы счисления © К.Ю. Поляков, 2007-2012 Тема 4. Шестнадцатеричная система счисления
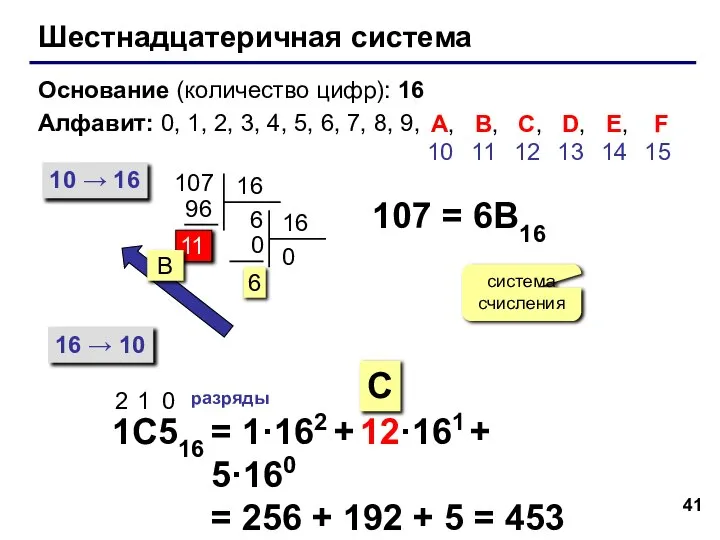
- 41. Шестнадцатеричная система Основание (количество цифр): 16 Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8,
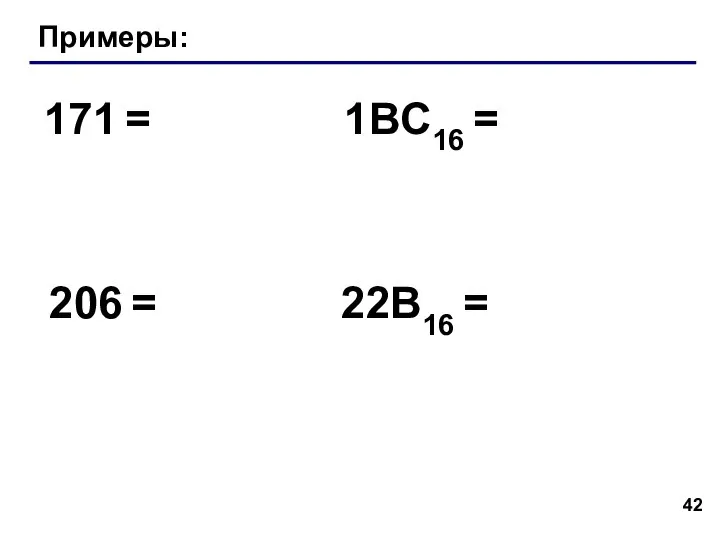
- 42. Примеры: 171 = 206 = 1BC16 = 22B16 =
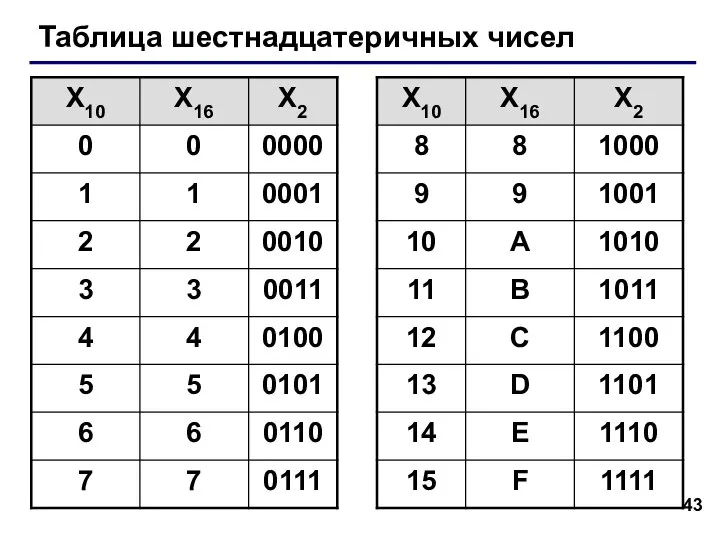
- 43. Таблица шестнадцатеричных чисел
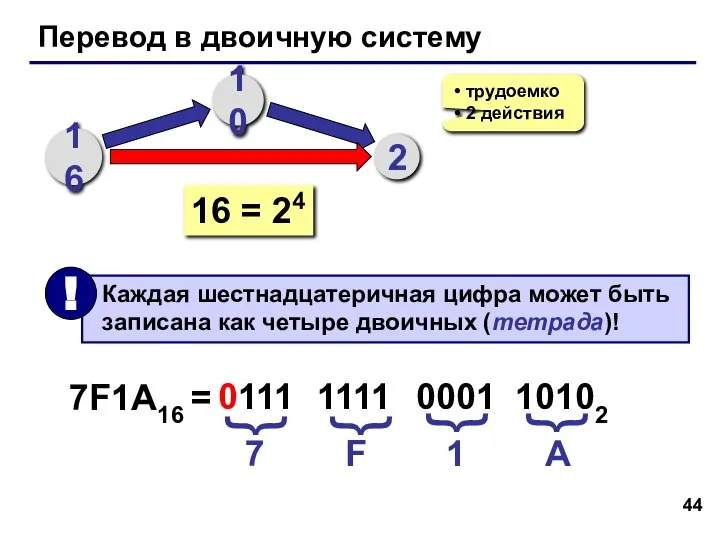
- 44. Перевод в двоичную систему 16 10 2 трудоемко 2 действия 16 = 24 7F1A16 = 7
- 45. Примеры: C73B16 = 2FE116 =
- 46. Перевод из двоичной системы 10010111011112 Шаг 1. Разбить на тетрады, начиная справа: 0001 0010 1110 11112
- 47. Примеры: 10101011010101102 = 1111001101111101012 = 1101101101011111102 =
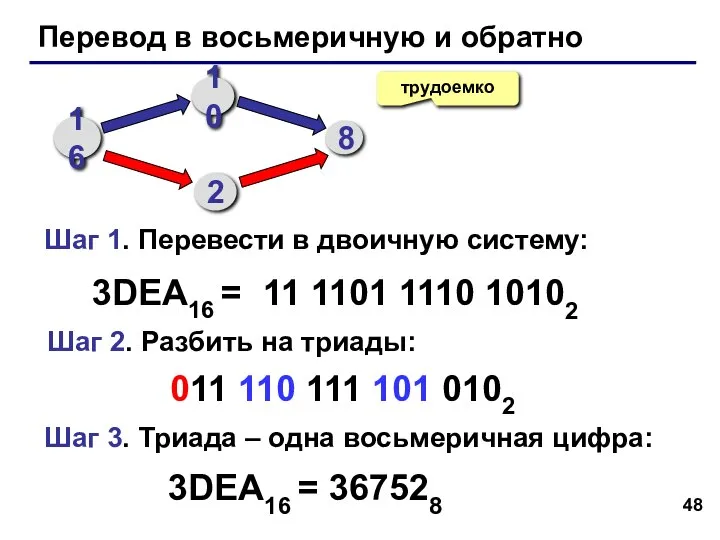
- 48. Перевод в восьмеричную и обратно трудоемко 3DEA16 = 11 1101 1110 10102 16 10 8 2
- 49. Примеры: A3516 = 7658 =
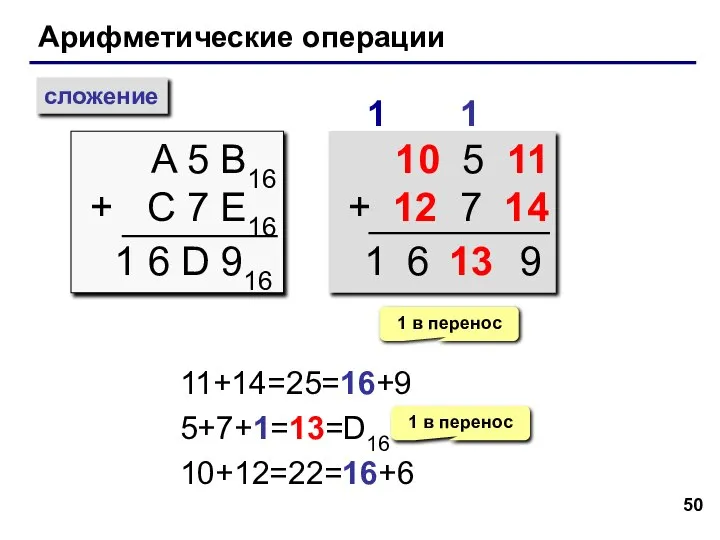
- 50. Арифметические операции сложение A 5 B16 + C 7 E16 1 1 6 D 916 10
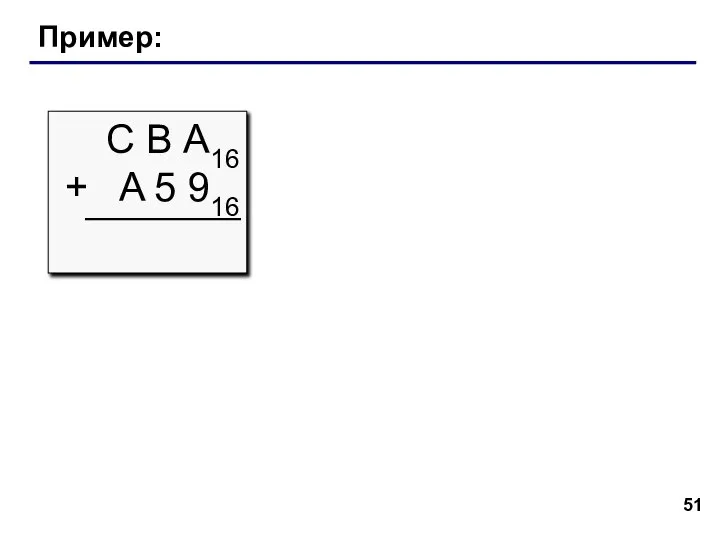
- 51. Пример: С В А16 + A 5 916
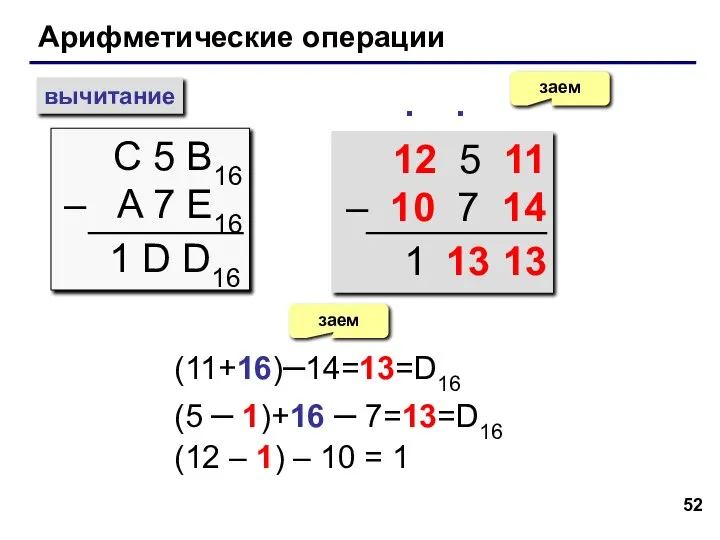
- 52. Арифметические операции вычитание С 5 B16 – A 7 E16 заем ∙ 1 D D16 12
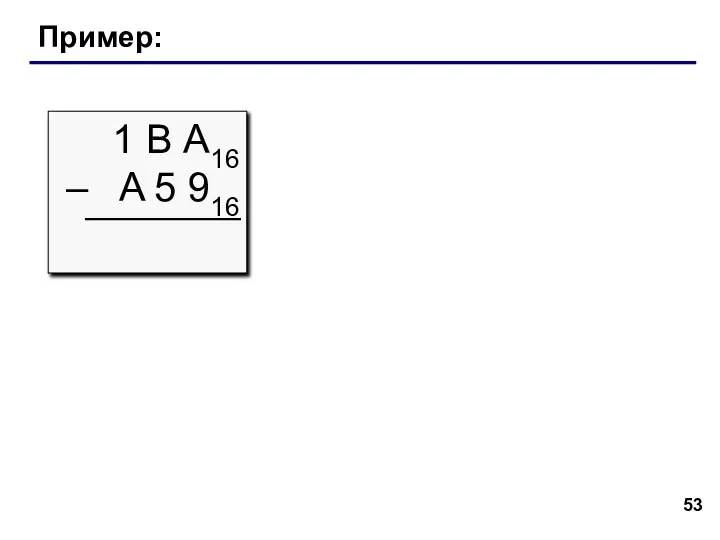
- 53. Пример: 1 В А16 – A 5 916
- 54. Системы счисления © К.Ю. Поляков, 2007-2012 Тема 5. Другие системы счисления
- 55. Троичная уравновешенная система Задача Баше: Найти такой набор из 4 гирь, чтобы с их помощью на
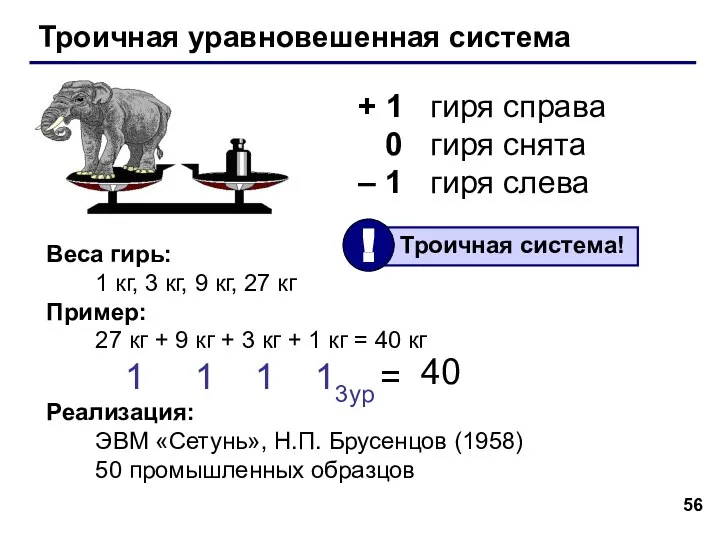
- 56. Троичная уравновешенная система + 1 гиря справа 0 гиря снята – 1 гиря слева Веса гирь:
- 58. Скачать презентацию































 Основы Network Access Protection
Основы Network Access Protection Распределение функциональных требований безопасности
Распределение функциональных требований безопасности Обеспечение технологической устойчивости объектов ДЭЗ за счёт внедрения цифровизации и передовых технологий
Обеспечение технологической устойчивости объектов ДЭЗ за счёт внедрения цифровизации и передовых технологий WORD. Работа с таблицей (меню и панель инструментов)
WORD. Работа с таблицей (меню и панель инструментов) Эвентос. Облачная платформа генерации семантического контента
Эвентос. Облачная платформа генерации семантического контента World Wide Web
World Wide Web Панель основных процессов (Basic Process)
Панель основных процессов (Basic Process) Заместитель (Proxy) или Сурогат (Surrogate)
Заместитель (Proxy) или Сурогат (Surrogate) Использование Linux при программировании 3
Использование Linux при программировании 3 Конкурс по поиску информации в интернете. Деловая игра
Конкурс по поиску информации в интернете. Деловая игра Android приложение Навигатор первокурсника
Android приложение Навигатор первокурсника Система счисления
Система счисления Введение в HTML. Основы WEB-технологий
Введение в HTML. Основы WEB-технологий Что пишут на C#
Что пишут на C# Операционная система Windows
Операционная система Windows Презентация на тему Внешняя память, её виды
Презентация на тему Внешняя память, её виды  Логические основы ЭВМ
Логические основы ЭВМ Теоретические основы компьютерной безопасности
Теоретические основы компьютерной безопасности Distributed computing and data processing frameworks
Distributed computing and data processing frameworks HDMI конвертеры (AV RCA)
HDMI конвертеры (AV RCA) Кроссворд с триггерами
Кроссворд с триггерами Автоматизированная система удаленного рабочего процесса сотрудников предприятия
Автоматизированная система удаленного рабочего процесса сотрудников предприятия Теория автоматов и формальных языков. Лекция 1
Теория автоматов и формальных языков. Лекция 1 Аккаунт экскурсовода-гида
Аккаунт экскурсовода-гида Digital parenting (цифровое воспитание)
Digital parenting (цифровое воспитание) Презентация на тему Развитие логического мышления на уроках информатики
Презентация на тему Развитие логического мышления на уроках информатики  Программное обеспечение ПК
Программное обеспечение ПК Галамарт | Челябинск-Курган
Галамарт | Челябинск-Курган