Содержание
- 2. – способ записи чисел с помощью заданного набора специальных знаков (цифр). – специальный язык, алфавитом которого
- 3. – возможность представления любого числа в рассматриваемом диапазоне величин; – единственность представления (каждой комбинации символов должна
- 4. Цифры – последовательность условных знаков для записи чисел. Сокращенная запись числа: A= an-1 an-2 ... ai
- 5. Система счисления Позиционная Непозиционная величина, которую обозначает цифра, не зависит от позиции цифры в записи числа
- 6. Уна́рная система счисления — положительная суммарная целочисленная система счисления с основанием, равным 1. Запись числа: где
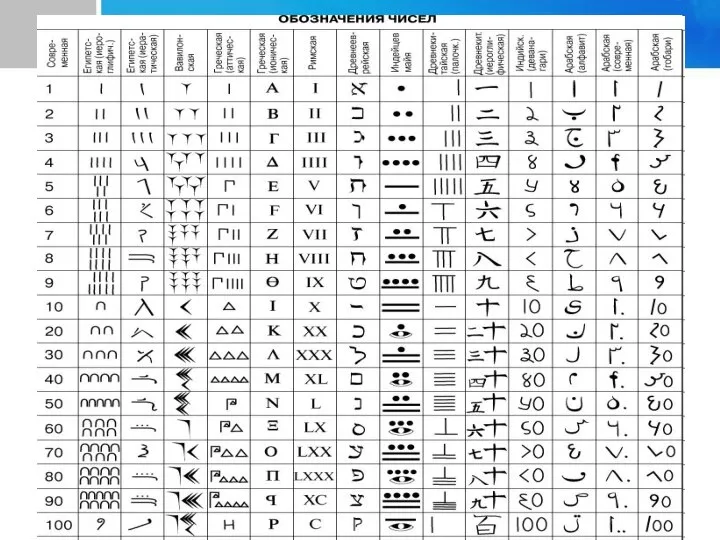
- 7. Единичная система (непозиционная) В древние времена, когда люди начали считать, появилась потребность в записи чисел. Первоначально
- 8. Система счисления древнего Египта 345 В древнеегипетской системе счисления, которая возникла во второй половине третьего тысячелетия
- 9. Цифры майя Другая система счисления основанная на позиционном принципе, возникла у индейцев майя, обитателей полуострова Юкатан
- 10. Вавилонская шестидесятиричная система счисления Числа в этой системе счисления составлялись из знаков двух видов: прямой клин
- 11. Все числа от 1 до 59 вавилоняне записывали в десятичной непозиционной системе, а число в целом
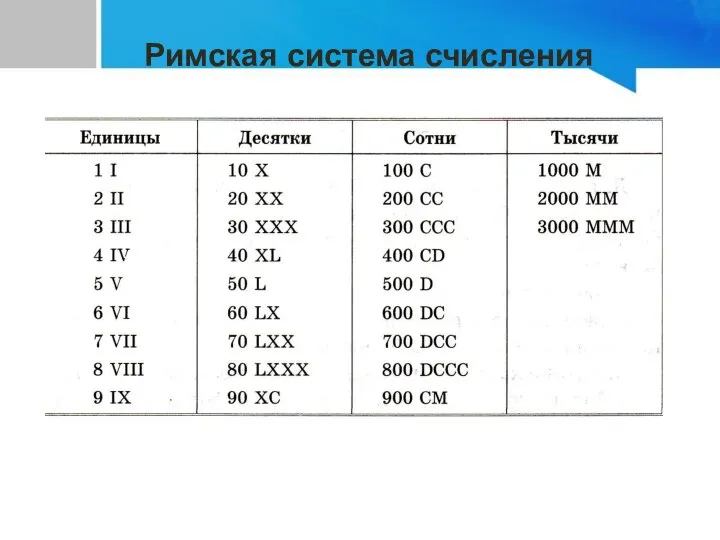
- 12. Римская система счисления
- 13. Сначала записывается число тысяч, затем сотен, затем десятков и единиц. Принцип сложения - если большая цифра
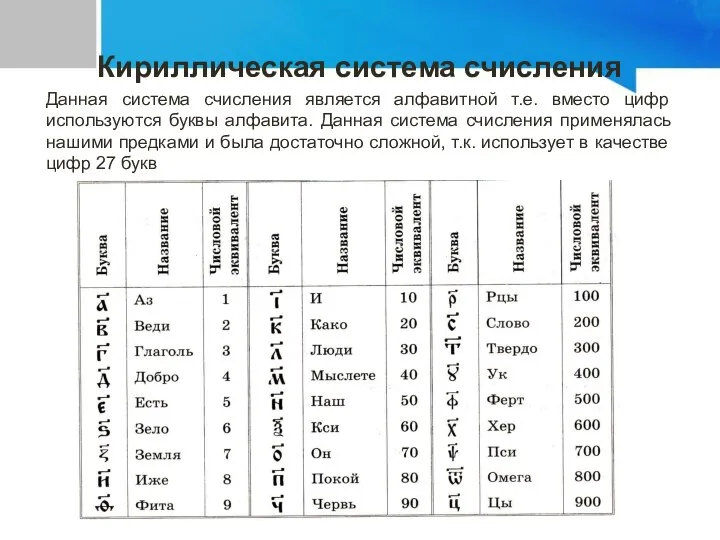
- 14. Кириллическая система счисления Данная система счисления является алфавитной т.е. вместо цифр используются буквы алфавита. Данная система
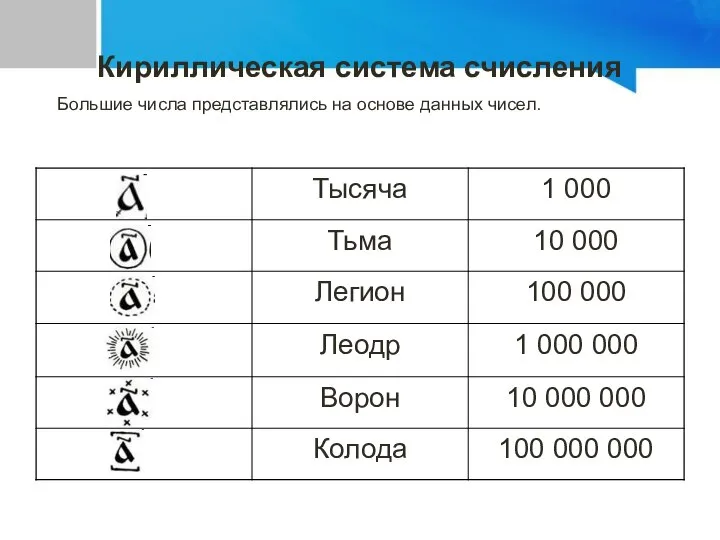
- 15. Кириллическая система счисления Большие числа представлялись на основе данных чисел.
- 16. Вот некоторые числа записанные в славянской системе счисления Данная система является непозиционной, т.е. число не зависит
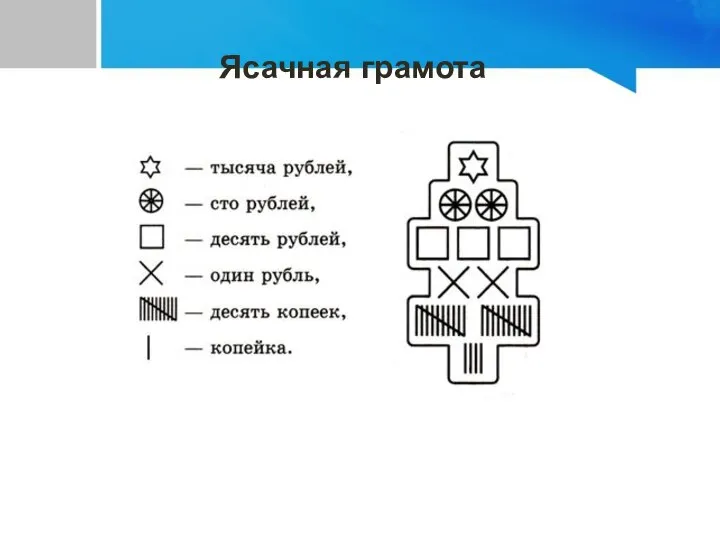
- 17. Ясачная грамота
- 19. Существует постоянная потребность введения новых знаков для записи больших чисел. Невозможно представлять дробные и отрицательные числа,
- 20. Основание - возводимое в степень целое число, равное количеству знаков или символов, используемых для изображения числа
- 21. Базис – последовательность чисел, каждое из которых задает количественное значение или "вес" каждого разряда. Десятичная система:100,101,102,103,104,...,10n,
- 22. Алфавит - совокупность различных цифр, используемых для записи чисел. Количество цифр в алфавите равно основанию системы
- 23. Развернутая форма представления числа: Аq=±(an-1qn-1+an-2qn-2+...+a0q0+a-1q-1+a-2q-2+...+a-mq-m), где А — само число, q — основание системы счисления, ai
- 24. Значение цифры на любой i-й позиции: aiqi, где i – номер позиции в числе, q –
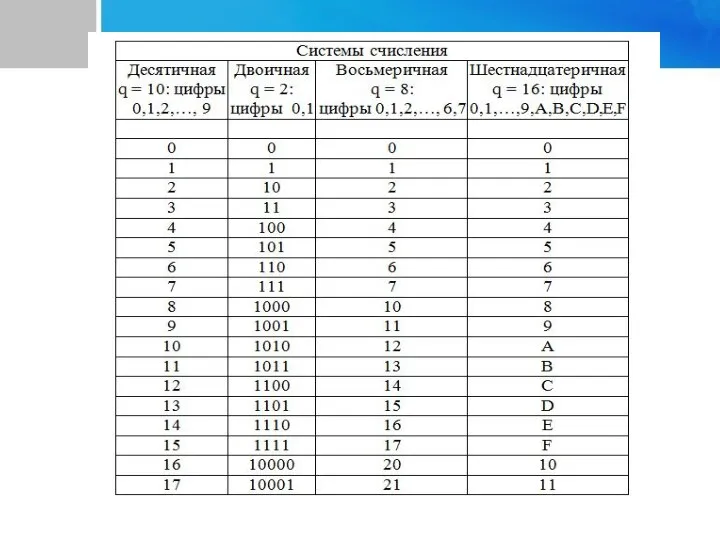
- 25. Свернутая форма представления числа: А=±an-1an-2...a0,a-1a-2...a-m (q) Название системы определяет ее основание q: десятичная, двоичная, восьмеричная и
- 26. Наличие физических элементов, способных изобразить символы системы. Экономичность системы, то есть количество элементов, необходимое для представления
- 27. Двоичная СС База двоичной системы счисления использует для изображения чисел только две цифры: аi = {0,1}.
- 28. Восьмеричная СС Восьмеричная и шестнадцатеричная системы счисления относятся к двоично-кодированным системам, когда основание системы счисления p
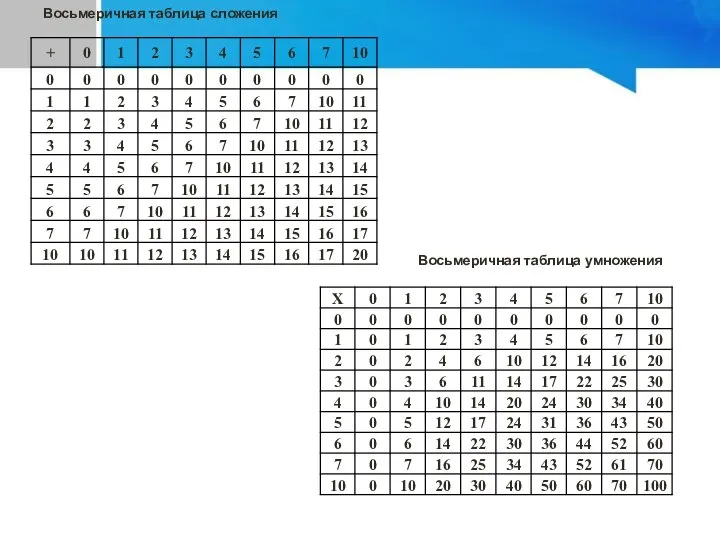
- 29. Восьмеричная таблица сложения Восьмеричная таблица умножения
- 30. Шестнадцатеричная СС В шестнадцатеричной системе для записи чисел используются цифры 0, 1, 2, 3, 4, 5,
- 31. Шестнадцатеричная таблица сложения
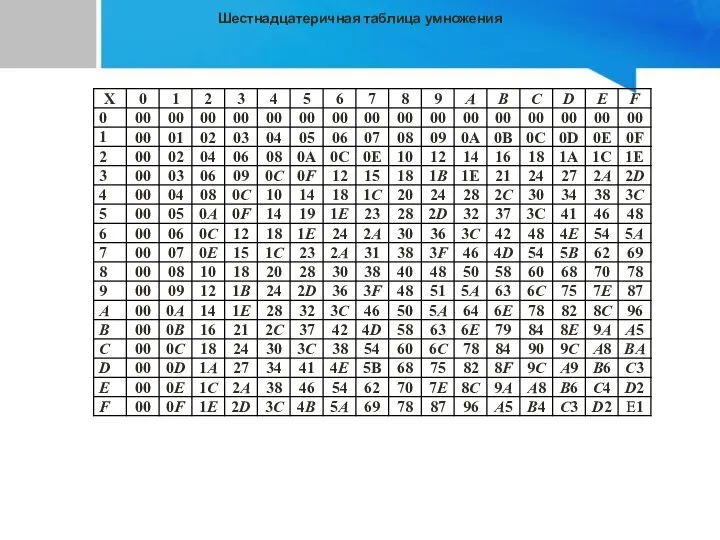
- 32. Шестнадцатеричная таблица умножения
- 34. Рассмотрим пример арифметических операций с двоичными числами Рассмотрим пример арифметических операций с 8-ричными и 16-ричными числами
- 35. Методы перевода чисел из одной СС в другую
- 36. Табличный метод Пример 1.1. Перевести число A = 238(10) в двоичную систему счисления: Решение. Подставив значение
- 38. Перевод целых чисел из одной системы счисления в другую Алгоритм перевода целых чисел из системы с
- 39. 1. Разделить исходное число A(p) на основание новой системы счисления, записанное в старой – q(p). Полученный
- 40. При переводе из двоичной системы счисления в десятичную исходное число необходимо делить на основание новой системы
- 41. Алгоритм перевода правильной дроби с основанием p в дробь с основанием q: Основание новой системы счисления
- 42. Умножить исходное число A(p) на основание новой системы счисления, записанное в старой – q(p). Целая часть
- 43. При переводе из двоичной системы в десятичную умножаем исходное число 0,1011(2 на 10(10) = 1010(2): 1
- 44. Перевод произвольных чисел, т.е. чисел, содержащих целую и дробную части, осуществляется в два этапа. Отдельно переводится
- 45. Пример 1.6. Перевести число A=139,6875(10) в двоичную систему счисления. Решение. а) При переводе из десятичной системы
- 46. Перевод чисел из системы счисления с основанием 2 в систему счисления с основанием 2n и обратно
- 47. Перевод целых чисел Двоичное число разбить справа налево на группы по n цифр в каждой. Если
- 48. Перевод дробных чисел: Двоичное число разбить слева направо на группы по n цифр в каждой. Если
- 49. Перевод чисел в кратных системах счисления Рассмотрим перевод числа из системы счисления с основанием p в
- 50. Перевод чисел в кратных системах счисления При переводе шестнадцатеричного числа F01,A(16) в двоичную систему счисления нужно
- 51. каждую цифру этого числа заменить ее n-значным эквивалентом в двоичной системе счисления. Перевод чисел из систем
- 53. Скачать презентацию









































 1.11_Многомерные _массивы (1)
1.11_Многомерные _массивы (1) Марафон “5 дней - 5 навыков”. Профессия “Удаленный помощник онлайн-предпринимателя”
Марафон “5 дней - 5 навыков”. Профессия “Удаленный помощник онлайн-предпринимателя” Дополнительные устройства компьютера
Дополнительные устройства компьютера Система счисления. Вопросы для повторения
Система счисления. Вопросы для повторения Система заказа и доставки продуктов. Детский интернет форум Цифровое поколение
Система заказа и доставки продуктов. Детский интернет форум Цифровое поколение Электронные таблицы (ЭТ)
Электронные таблицы (ЭТ) Каскадные таблицы стилей (CSS)
Каскадные таблицы стилей (CSS) 1с: бухгалтерия
1с: бухгалтерия Эффективный PR образовательных организаций в социальных сетях
Эффективный PR образовательных организаций в социальных сетях Система документирования радиолокационной информации
Система документирования радиолокационной информации Как привязать учетную запись СГО к порталу Госуслуг
Как привязать учетную запись СГО к порталу Госуслуг Алгоритмы с ветвлением
Алгоритмы с ветвлением Сетевые технологии. Структура URL
Сетевые технологии. Структура URL Презентация на тему Хранение информации. Действия с информацией
Презентация на тему Хранение информации. Действия с информацией  ec8f84f81f5c61f5
ec8f84f81f5c61f5 StyleOut. Запуск рекламы
StyleOut. Запуск рекламы Цикл for
Цикл for Информатика
Информатика 1С; управление лагерем 11
1С; управление лагерем 11 Модуль tKinter
Модуль tKinter Web-ресурсы полезные для бухгалтера
Web-ресурсы полезные для бухгалтера ИГРА ПО БЕЗОПАСНОСТИ ДЕТЕЙ В ИНТЕРНЕТ ПРОСТРАНСТВЕ ДЕТИ В ИНТЕРНЕТЕ
ИГРА ПО БЕЗОПАСНОСТИ ДЕТЕЙ В ИНТЕРНЕТ ПРОСТРАНСТВЕ ДЕТИ В ИНТЕРНЕТЕ Operators and Expression / 1 of 25
Operators and Expression / 1 of 25 Вход в личный кабинет
Вход в личный кабинет Общие требования к структуре и содержанию электронного образовательного ресурса
Общие требования к структуре и содержанию электронного образовательного ресурса Модификации, ставшие полноценными играми
Модификации, ставшие полноценными играми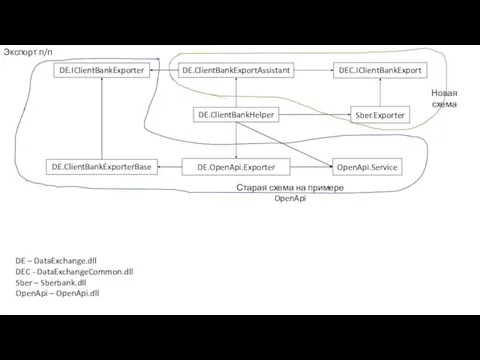 Export flow для Сбера
Export flow для Сбера Python. Введение
Python. Введение