Содержание
- 2. Системы счисления Тема 1. Введение
- 3. Определения Система счисления – это способ записи чисел с помощью специальных знаков – цифр. Числа: 123,
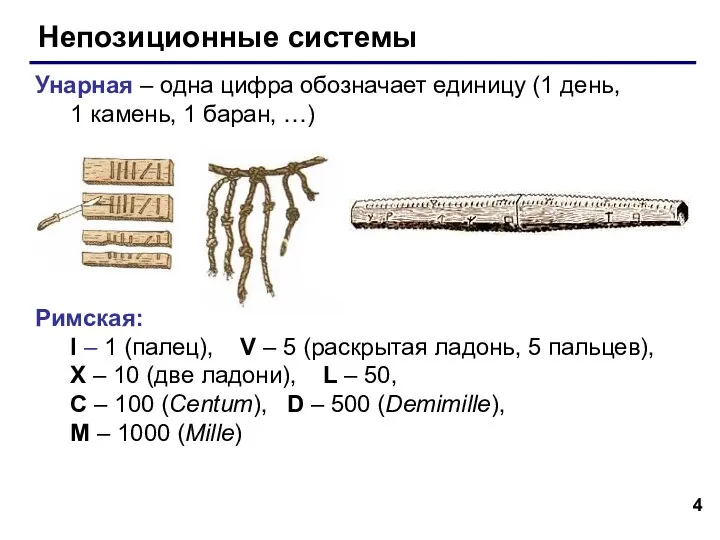
- 4. Непозиционные системы Унарная – одна цифра обозначает единицу (1 день, 1 камень, 1 баран, …) Римская:
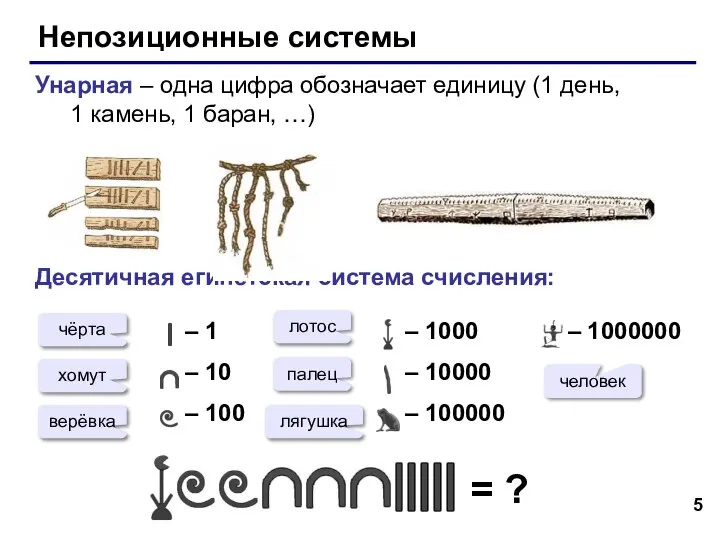
- 5. Непозиционные системы Унарная – одна цифра обозначает единицу (1 день, 1 камень, 1 баран, …) Десятичная
- 6. Непозиционные системы Римская система счисления: I – 1 (палец), V – 5 (раскрытая ладонь, 5 пальцев),
- 7. Римская система счисления Правила: (обычно) не ставят больше трех одинаковых цифр подряд если младшая цифра (только
- 8. Примеры: 3768 = 2983 = 1452 = 1999 =
- 9. Римская система счисления Недостатки: для записи больших чисел (>3999) надо вводить новые знаки-цифры (V, X, L,
- 10. Славянская система счисления алфавитная система счисления (непозиционная) Часы Суздальского Кремля
- 11. Позиционные системы Позиционная система: значение цифры определяется ее позицией в записи числа. Десятичная система: первоначально –
- 12. Позиционные системы Задача: в какой системе счисления число 58 записывается как «46x»? Определите основание системы счисления
- 13. Позиционные системы Задача: найдите основание системы счисления, в которой выполняется равенство в записи есть цифра 5,
- 14. Позиционные системы Задача: перечислите через запятую все системы счисления, в которых выполняется неравенство в записи есть
- 15. Системы счисления Тема 2. Двоичная система счисления
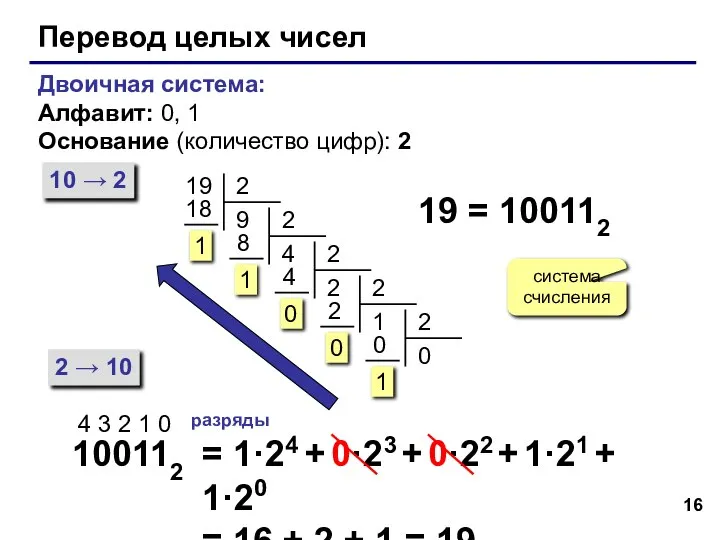
- 16. Перевод целых чисел Двоичная система: Алфавит: 0, 1 Основание (количество цифр): 2 10 → 2 2
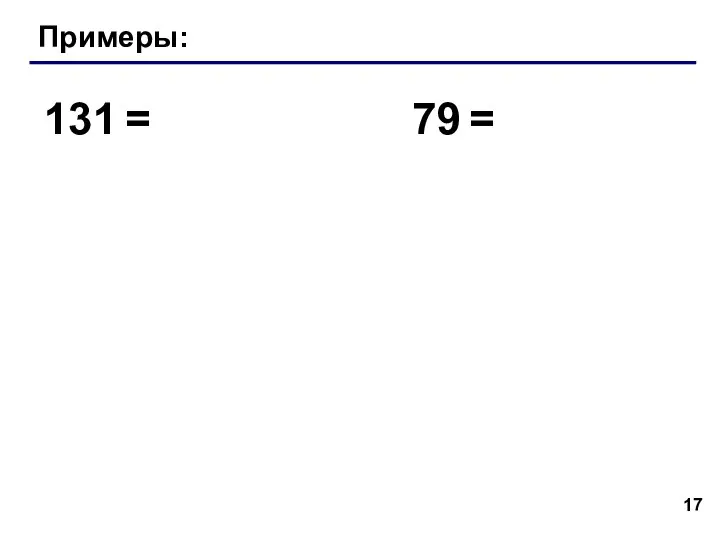
- 17. Примеры: 131 = 79 =
- 18. Примеры: 1010112 = 1101102 =
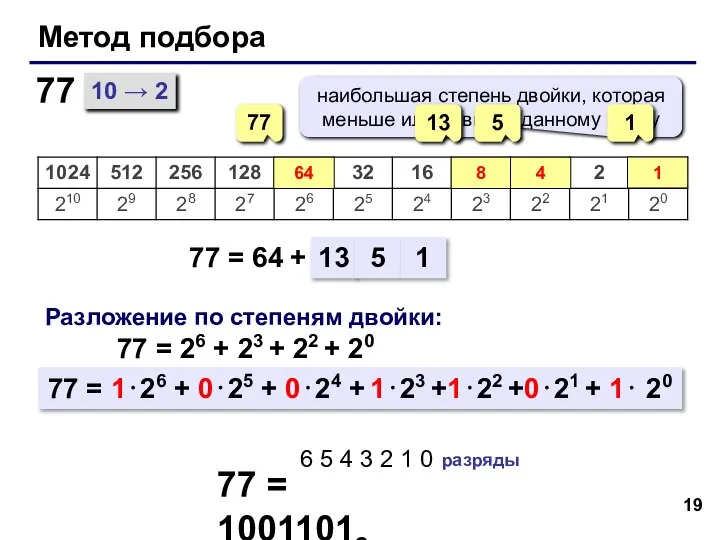
- 19. Метод подбора 10 → 2 77 = 64 + 77 77 64 Разложение по степеням двойки:
- 20. Перевод дробных чисел 10 → 2 2 → 10 0,375 = × 2 101,0112 2 1
- 21. Примеры: 0,625 = 3,875 =
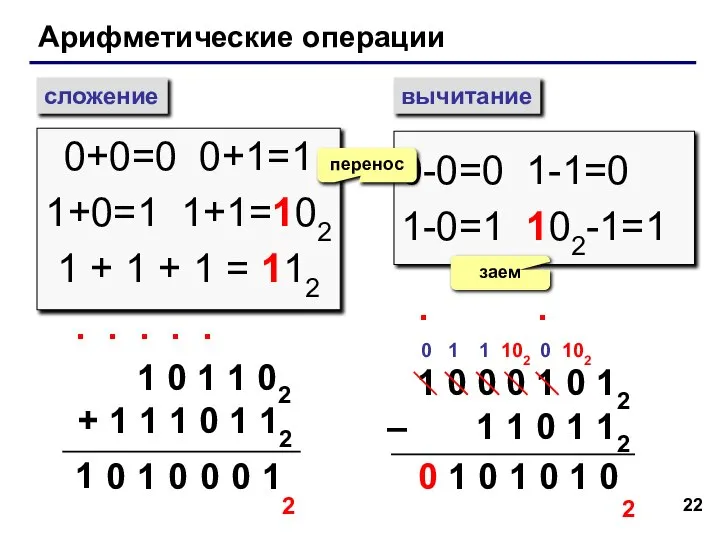
- 22. Арифметические операции сложение вычитание 0+0=0 0+1=1 1+0=1 1+1=102 1 + 1 + 1 = 112 0-0=0
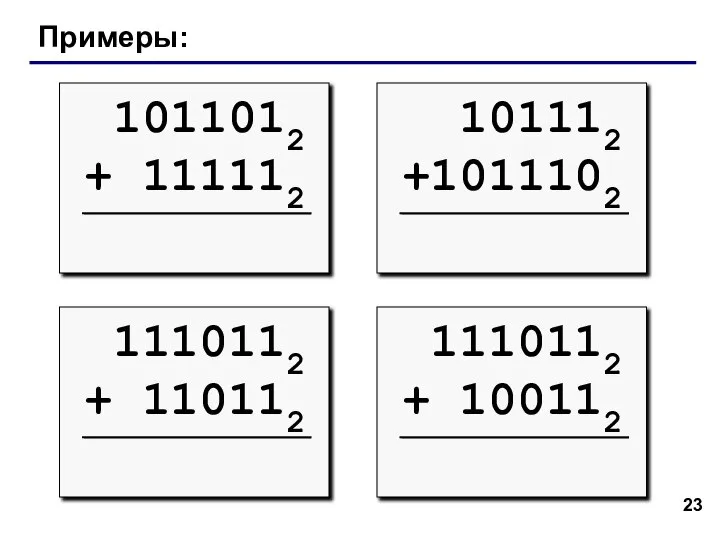
- 23. Примеры:
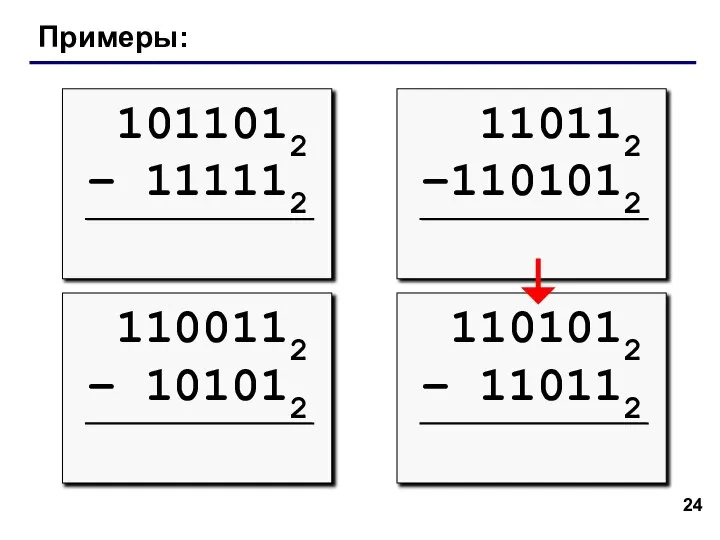
- 24. Примеры:
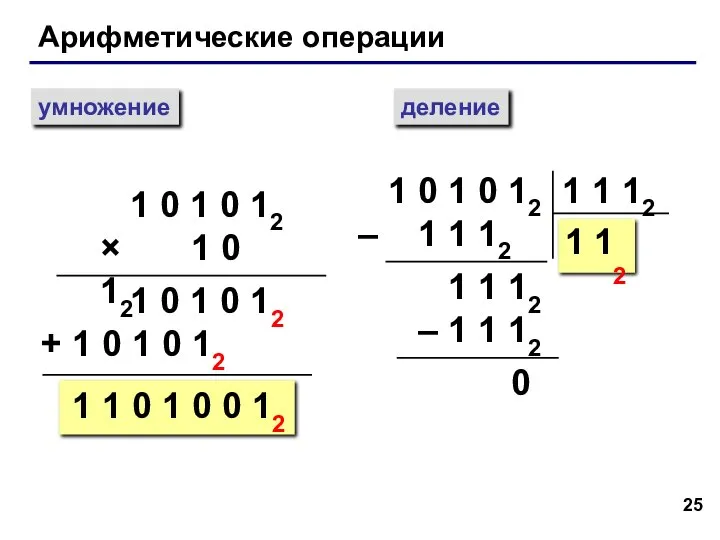
- 25. Арифметические операции умножение деление 1 0 1 0 12 × 1 0 12 1 0 1
- 26. Плюсы и минусы двоичной системы нужны технические устройства только с двумя устойчивыми состояниями (есть ток —
- 27. Двоично-десятичная система BCD = binary coded decimals (десятичные цифры в двоичном коде) 9024,19 = 1001 0000
- 28. Системы счисления Тема 3. Восьмеричная система счисления
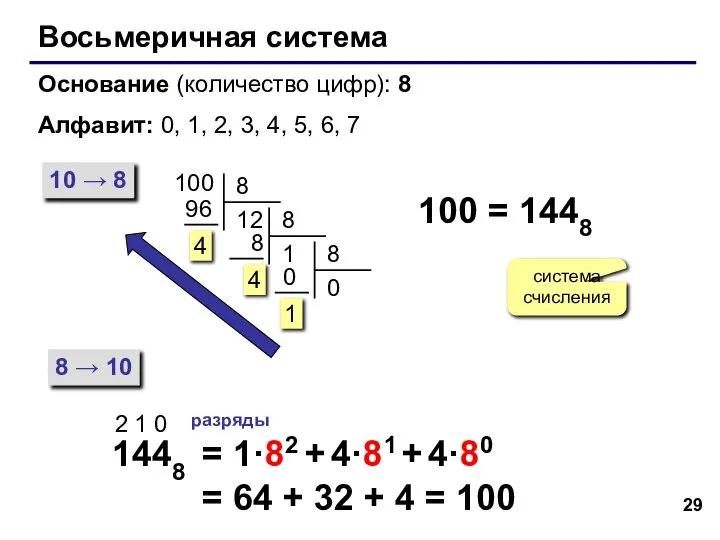
- 29. Восьмеричная система Основание (количество цифр): 8 Алфавит: 0, 1, 2, 3, 4, 5, 6, 7 10
- 30. Примеры: 134 = 75 = 1348 = 758 =
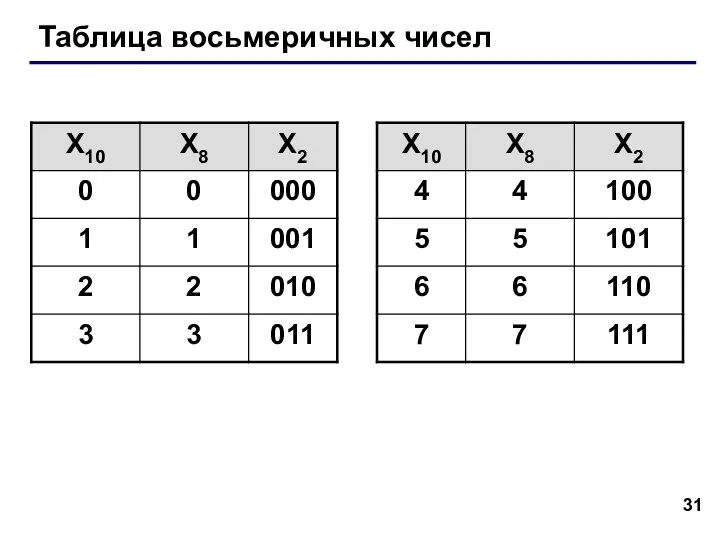
- 31. Таблица восьмеричных чисел
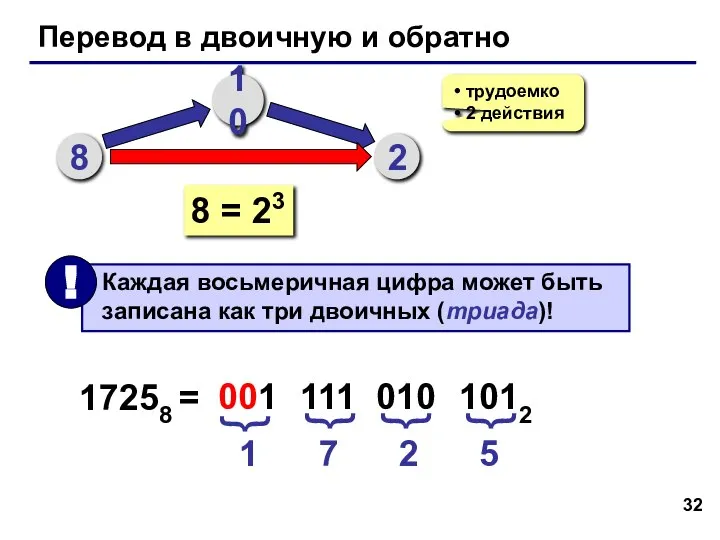
- 32. Перевод в двоичную и обратно 8 10 2 трудоемко 2 действия 8 = 23 17258 =
- 33. Примеры: 34678 = 21488 = 73528 = 12318 =
- 34. Перевод из двоичной системы 10010111011112 Шаг 1. Разбить на триады, начиная справа: 001 001 011 101
- 35. Примеры: 1011010100102 = 111111010112 = 11010110102 =
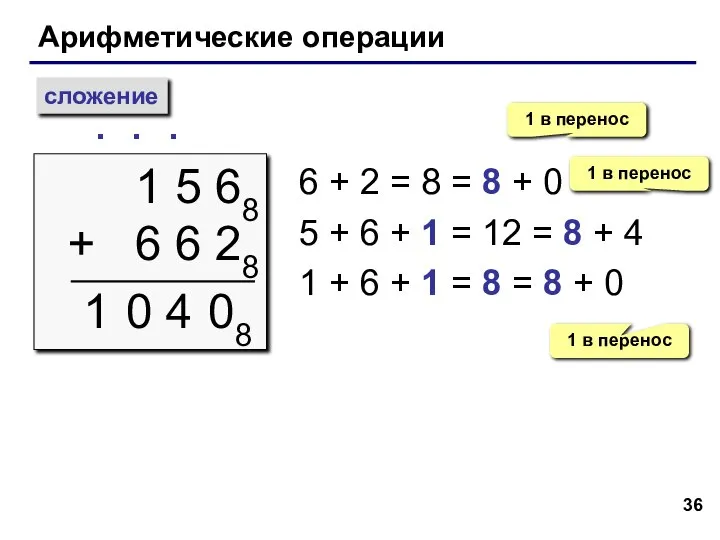
- 36. Арифметические операции сложение 1 5 68 + 6 6 28 ∙ 1 6 + 2 =
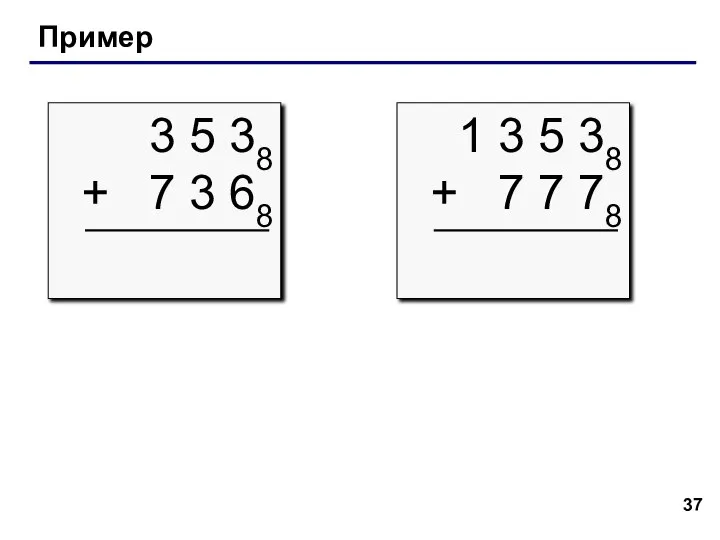
- 37. Пример
- 38. Арифметические операции вычитание 4 5 68 – 2 7 78 ∙ (6 + 8) – 7
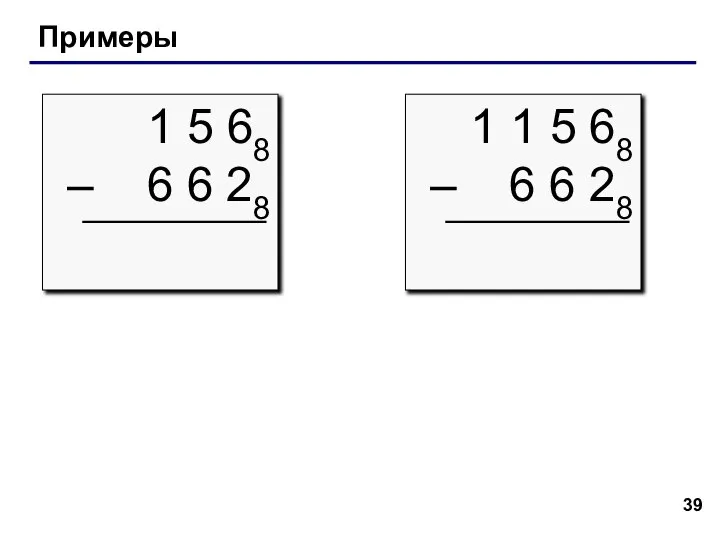
- 39. Примеры
- 40. Системы счисления Тема 4. Шестнадцатеричная система счисления
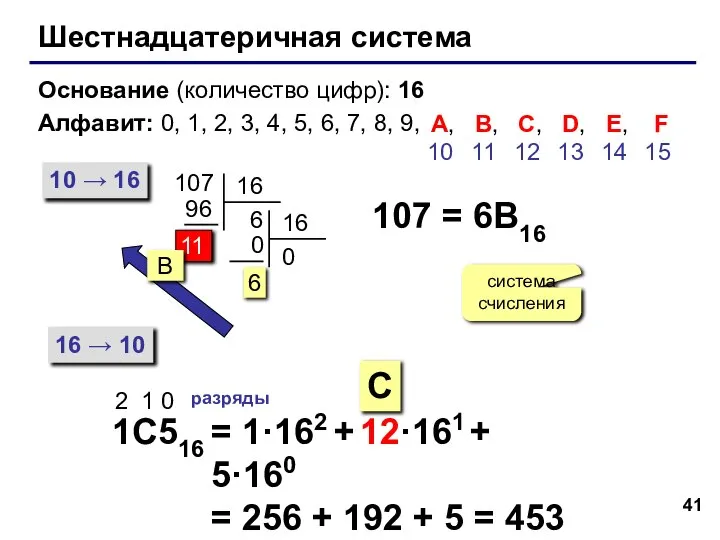
- 41. Шестнадцатеричная система Основание (количество цифр): 16 Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8,
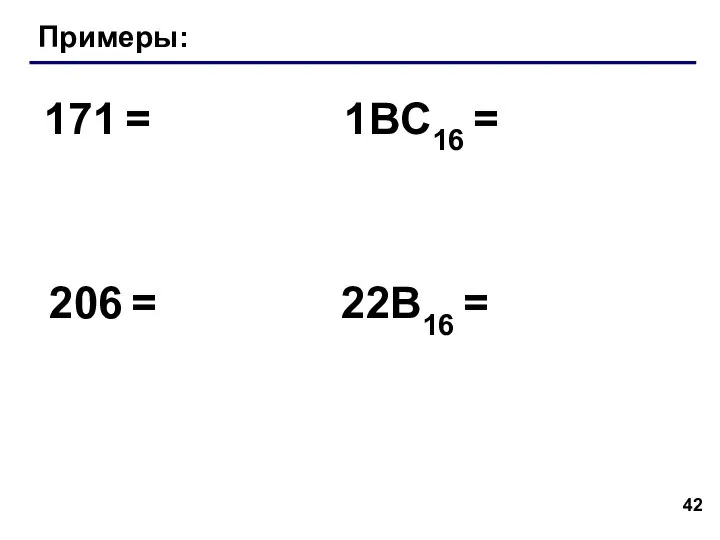
- 42. Примеры: 171 = 206 = 1BC16 = 22B16 =
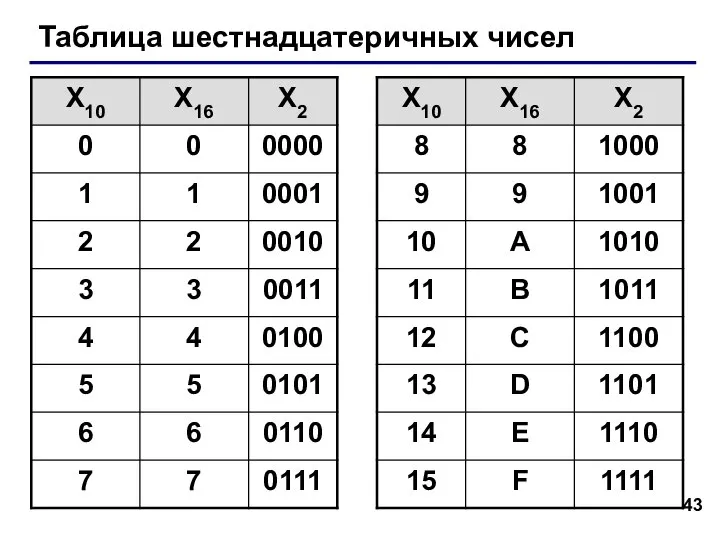
- 43. Таблица шестнадцатеричных чисел
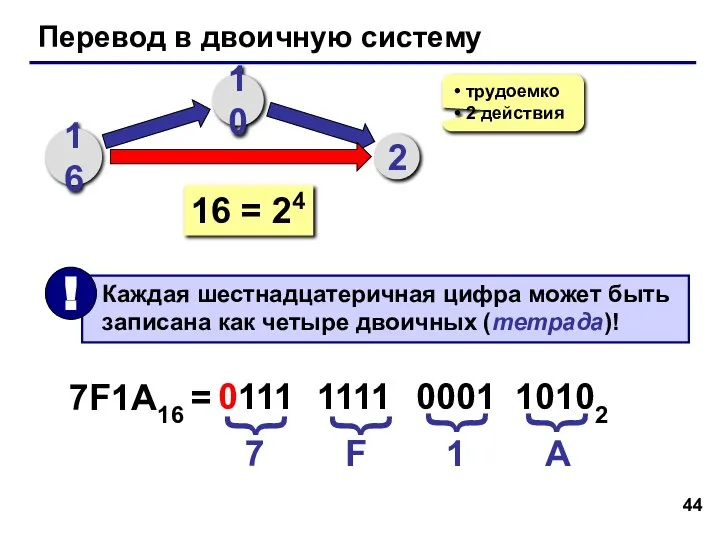
- 44. Перевод в двоичную систему 16 10 2 трудоемко 2 действия 16 = 24 7F1A16 = 7
- 45. Примеры: C73B16 = 2FE116 =
- 46. Перевод из двоичной системы 10010111011112 Шаг 1. Разбить на тетрады, начиная справа: 0001 0010 1110 11112
- 47. Примеры: 10101011010101102 = 1111001101111101012 = 1101101101011111102 =
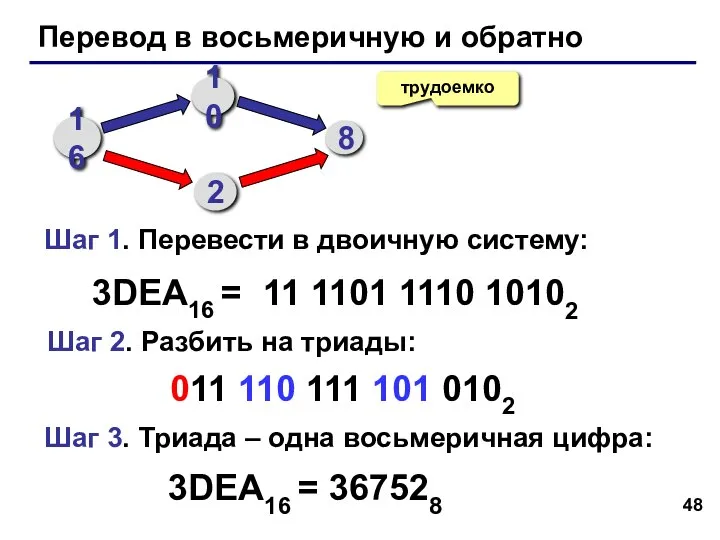
- 48. Перевод в восьмеричную и обратно трудоемко 3DEA16 = 11 1101 1110 10102 16 10 8 2
- 49. Примеры: A3516 = 7658 =
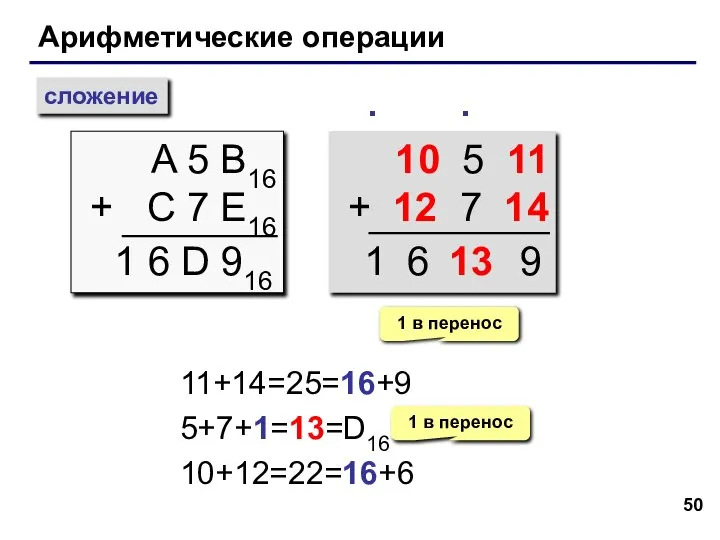
- 50. Арифметические операции сложение A 5 B16 + C 7 E16 ∙ 1 6 D 916 10
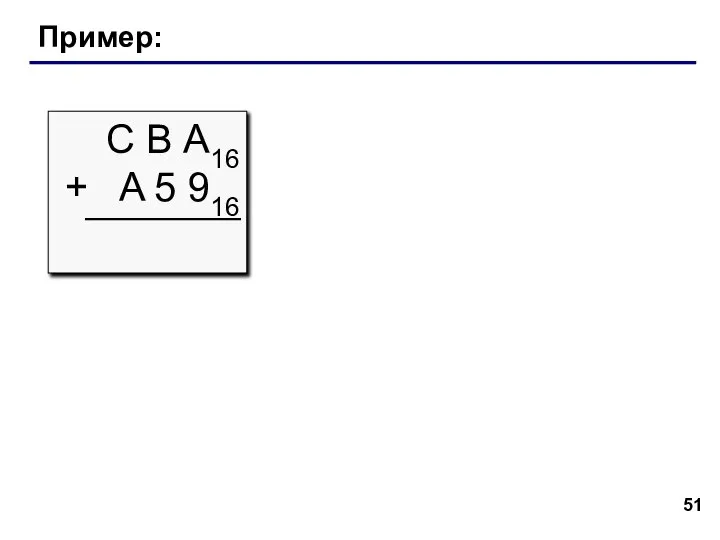
- 51. Пример: С В А16 + A 5 916
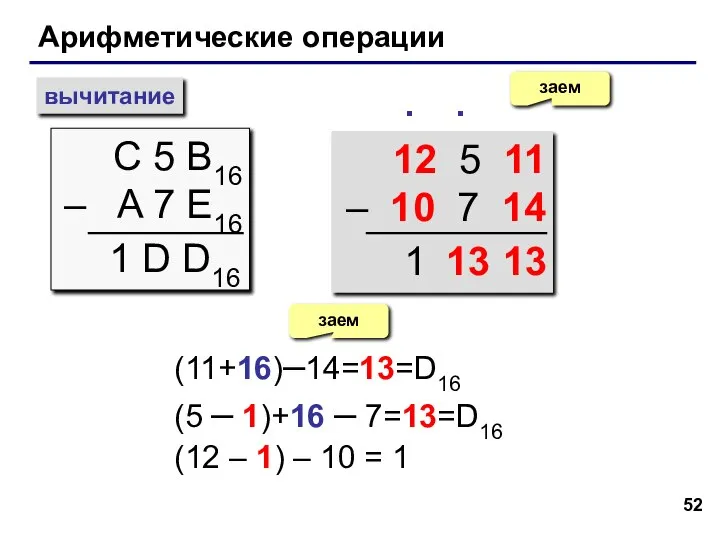
- 52. Арифметические операции вычитание С 5 B16 – A 7 E16 заем ∙ 1 D D16 12
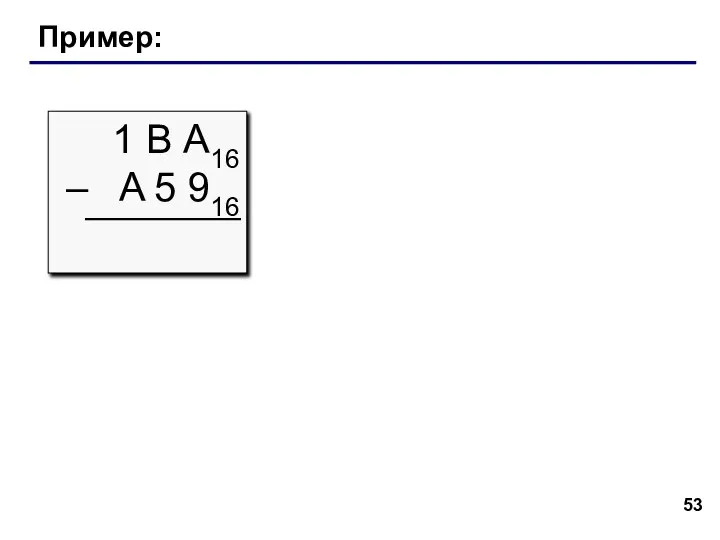
- 53. Пример: 1 В А16 – A 5 916
- 54. Системы счисления © К.Ю. Поляков, 2007-2012 Тема 5. Другие системы счисления
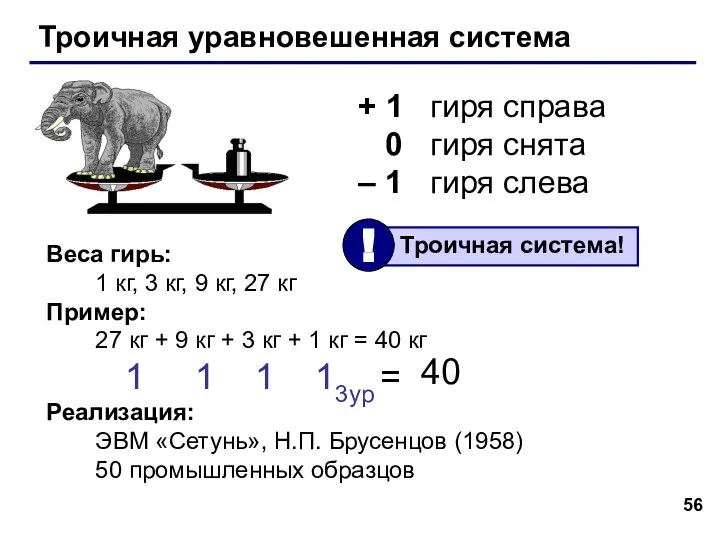
- 55. Троичная уравновешенная система Задача Баше: Найти такой набор из 4 гирь, чтобы с их помощью на
- 56. Троичная уравновешенная система + 1 гиря справа 0 гиря снята – 1 гиря слева Веса гирь:
- 58. Скачать презентацию






























 Введение в web-разработку
Введение в web-разработку Базы данных - основа информационной системы
Базы данных - основа информационной системы Изменение формы представления информации
Изменение формы представления информации Одномерные массивы
Одномерные массивы Методы и средства обеспечения безопасности
Методы и средства обеспечения безопасности Осторожно вирус! Все мы во власти интернета
Осторожно вирус! Все мы во власти интернета Сортировка вставками
Сортировка вставками Сетевые устройства
Сетевые устройства Правила оформления и публикации постов РДШ
Правила оформления и публикации постов РДШ Ссылки – теория
Ссылки – теория Объект и его свойства
Объект и его свойства Операционная система Windows
Операционная система Windows Управление наружным освещением с помощью системы Инфосфера
Управление наружным освещением с помощью системы Инфосфера Однозначное декодирование
Однозначное декодирование Регистрация ККТ в Личном кабинете ИП
Регистрация ККТ в Личном кабинете ИП Язык Basic. Технология разработки программного обеспечения
Язык Basic. Технология разработки программного обеспечения 5ee98598-9c1f-44e5-8384-12af453b45e3
5ee98598-9c1f-44e5-8384-12af453b45e3 Аналіз трактування медіаосвіти науковцями
Аналіз трактування медіаосвіти науковцями Графические информационные модели. К уроку информатики в 9 классе
Графические информационные модели. К уроку информатики в 9 классе Расширенная подписка на диагностическое программное обеспечение Bosch ESI[tronic] на специальных условиях
Расширенная подписка на диагностическое программное обеспечение Bosch ESI[tronic] на специальных условиях JS2 (JavaScript)
JS2 (JavaScript) Графический учебный исполнитель Стрелочка
Графический учебный исполнитель Стрелочка Дистанционное обучение
Дистанционное обучение Использование информационных технологий на уроках ненецкого языка в начальной школе
Использование информационных технологий на уроках ненецкого языка в начальной школе Цветокоррекция
Цветокоррекция Основные этапы информатизации общества
Основные этапы информатизации общества Тестирование методом черного ящика
Тестирование методом черного ящика Сказка Курочка ряба
Сказка Курочка ряба