Слайд 2Двоичная система счисления
В двоичной системе счисления используются всего две цифры 0 и

1. Другими словами, двойка является основанием двоичной системы счисления.
В двоичной системе счисления в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.
Слайд 3Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и

это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.
Слайд 4Перевод чисел из двоичной системы счисления в десятичную
Не трудно заметить, что в

двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.
Слайд 5В десятичной системе счисления любое число можно представить в форме суммы единиц,

десяток, сотен и т.д. Например:
1476 = 1000 + 400 + 70 + 6
Можно пойти еще дальше и разложить так:
1476 = 1 * 10^3 + 4 * 10^2 + 7 * 10^1 + 6 * 10^0
Слайд 6Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6

- это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.
Слайд 7Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:

10001001 = 1*2^7 + 0*2^6 + 0*2^5 + 0*2^4 + 1*2^3 + 0*2^2 + 0*2^1 + 1*2^0
Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:
1*2^7 + 0*2^6 + 0*2^5 + 0*2^4 + 1*2^3 + 0*2^2 + 0*2^1 + 1*2^0 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137
Слайд 8число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать

это можно так:
100010012 = 13710
Слайд 9Перевод десятичного числа в двоичное
Может потребоваться перевести десятичное число в двоичное. Один

из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:
77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)
Слайд 10Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77

в двоичном представлении. Проверим:
1001101 = 1*2^6 + 0*2^5 + 0*2^4 + 1*2^3 + 1*2^2 + 0*2^1 + 1*2^0 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77
Слайд 11Восьмеричная система счисления
Итак, современное «железо понимает» лишь двоичную систему счисления. Однако человеку

трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.
Слайд 12В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой

цифре соответствуют набор из трех цифр в двоичной системе счисления:
000 – 0
001 – 1
010 – 2
011 – 3
100 – 4
101 – 5
110 – 6
111 – 7
Слайд 13Для преобразования двоичного числа в восьмеричное достаточно разбить его на тройки и

заменить их соответствующими им цифрами из восьмеричной системы счисления. Разбивать на тройки нужно начинать с конца, а недостающие цифры в начале заменить нулями. Например:
1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135
Слайд 14Число 1011101 в двоичной системе счисления равно числу 135 в восьмеричной системе

счисления. Или 10111012 = 1358.
Обратный перевод. Допустим, требуется перевести число 1008 (не заблуждайтесь! 100 в восьмеричной системе – это не 100 в десятичной) в двоичную систему счисления.
1008 = 1 0 0 = 001 000 000 = 001000000 = 10000002
Слайд 15Перевод восьмеричного числа в десятичное можно осуществить по уже знакомой схеме:
6728 = 6

* 8^2 + 7 * 8^1 + 2 * 8^0 = 6 * 64 + 56 + 2 = 384 + 56 + 2 = 44210
1008 = 1 * 8^2 + 0 * 8^1 + 0 * 8^0 = 6410
Слайд 16Шестнадцатеричная система счисления
Шестнадцатеричная система счисления, так же как и восьмеричная, широко используется

в компьютерной науке из-за легкости перевода в нее двоичных чисел. При шестнадцатеричной записи числа получаются более компактными.
Слайд 17В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть

первых латинских букв – A (10), B (11), C (12), D (13), E (14), F (15).
При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди.
Слайд 18Каждой четверке соответствует цифра шестнадцатеричной системе счисления:
Например:
10011000101 = 0100 1100 0101 =

4 C 5 = 4C5
Если потребуется, то число 4C5 можно перевести в десятичную систему счисления следующим образом (C следует заменить на соответствующее данному символу число в десятичной системе счисления – это 12):
4C5 = 4 * 16^2 + 12 * 16^1 + 5 * 16^0 = 4 * 256 + 192 + 5 = 1221
Слайд 19Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи - это

FF.
FF = 15 * 161 + 15 * 160 = 240 + 15 = 255
255 – это максимальное значение одного байта, равного 8 битам: 1111 1111 = FF. Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255.


















 Программа для создания текстовых документов
Программа для создания текстовых документов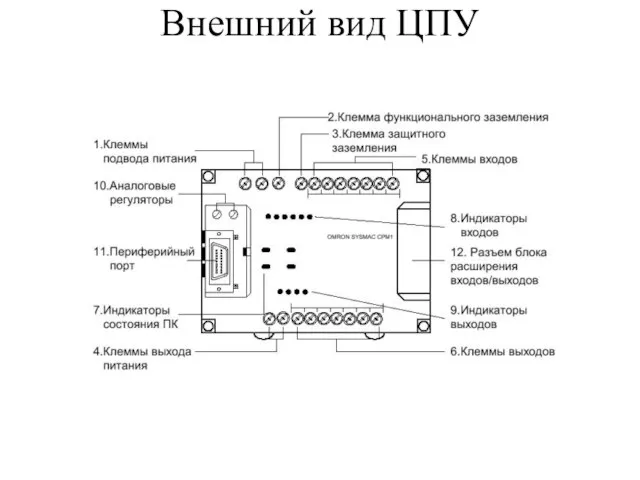 Внешний вид ЦПУ
Внешний вид ЦПУ Ithub-1. Поиск утечек персональных данных
Ithub-1. Поиск утечек персональных данных Процедуры в Turbo Pascalе
Процедуры в Turbo Pascalе SparkML basics
SparkML basics Разработка автоматизированного рабочего места экономиста по мониторингу товарных групп (на материалах Кормянского райпо)
Разработка автоматизированного рабочего места экономиста по мониторингу товарных групп (на материалах Кормянского райпо) Современные технологии эффективных закупок
Современные технологии эффективных закупок Урок 6. Центральные устройства компьютера (дз)
Урок 6. Центральные устройства компьютера (дз) Культура конкурсного поведения
Культура конкурсного поведения 10_klass_10-15_Programmirovanie_vetvleniy (1)
10_klass_10-15_Programmirovanie_vetvleniy (1) Секретарь онлайн-проектов. Что это за профессия?
Секретарь онлайн-проектов. Что это за профессия? Технологии программирования (лекция 3 )
Технологии программирования (лекция 3 ) Программное обеспечение компьютера. Операционная система
Программное обеспечение компьютера. Операционная система Запись ребенка в ДСУ на кружки
Запись ребенка в ДСУ на кружки Программное обеспечение в строительном проектировании
Программное обеспечение в строительном проектировании Генератор случайных чисел. Повторение. Lazarus
Генератор случайных чисел. Повторение. Lazarus Лекция 1 для МиКвКС
Лекция 1 для МиКвКС Обработка символьной информации в языке Pascal
Обработка символьной информации в языке Pascal Ваш выбор. Тест
Ваш выбор. Тест Село Каракулино — школа для обучающихся с ОВЗ
Село Каракулино — школа для обучающихся с ОВЗ Презентация на тему Блок схемы
Презентация на тему Блок схемы  Вход в систему ПАК РМК
Вход в систему ПАК РМК This is Your Presentation Title
This is Your Presentation Title Обработка ошибок
Обработка ошибок Буктрейлер. Титры и авторское право. Обучающий материал для подготовки буктрейлера
Буктрейлер. Титры и авторское право. Обучающий материал для подготовки буктрейлера Презентация — это не слайды!
Презентация — это не слайды!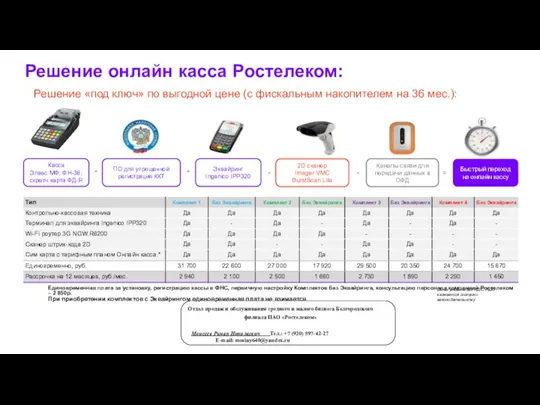 Решение под ключ по выгодной цене с фискальным накопителем на 36 месяцев, онлайн касса Ростелеком
Решение под ключ по выгодной цене с фискальным накопителем на 36 месяцев, онлайн касса Ростелеком Новые поколения ЭВМ. Нейрокомпьютеры
Новые поколения ЭВМ. Нейрокомпьютеры