Содержание
- 2. Виды информации по ее форме представления цифровая; текстовая; звуковая; графическая; видеоинформация
- 3. ВИЛЬГЕЛЬМ ЛЕЙБНИЦ (1646-1716) Возможность представления информации двоичными цифрами
- 4. N = 2m, где N – количество независимых кодируемых значений; m – разрядность двоичного кодирования 0
- 5. Единицы измерения информации: 1 бит =1 двоичный разряд= 0 или 1. 1 байт=8 бит(byte), количество битов,
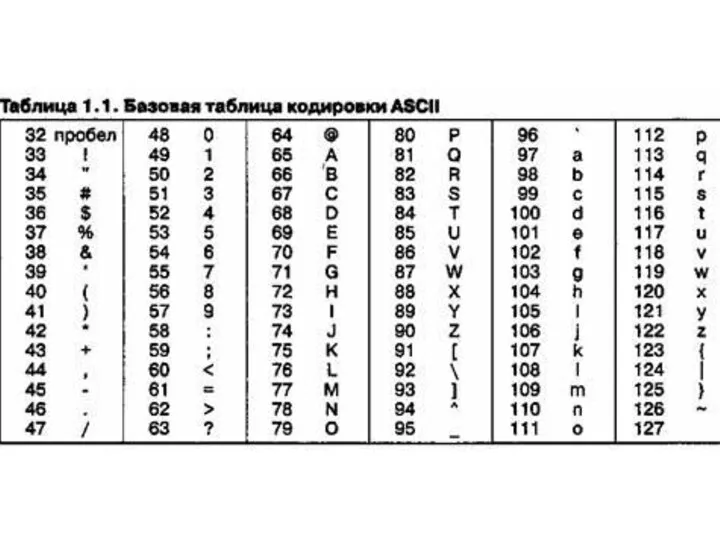
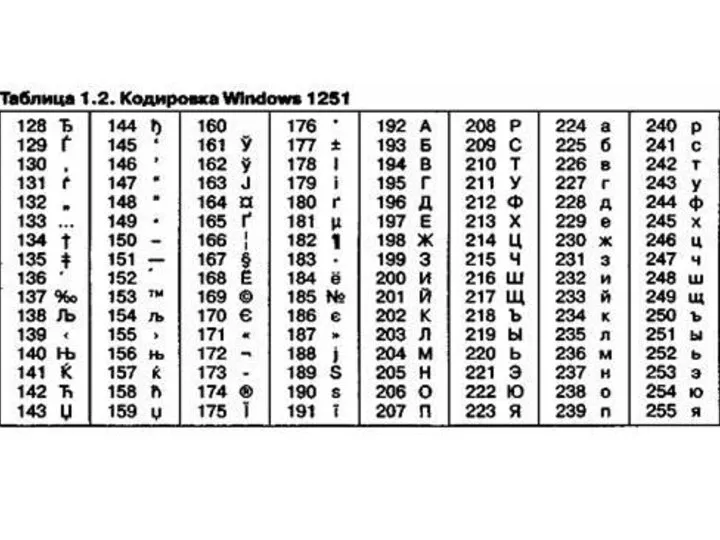
- 6. КОДИРОВАНИЕ ТЕКСТОВЫХ ДАННЫХ ASCII Windows-1251 КОИ-8 ISO ГОСТ и ГОСТ-альтернативная Unicode
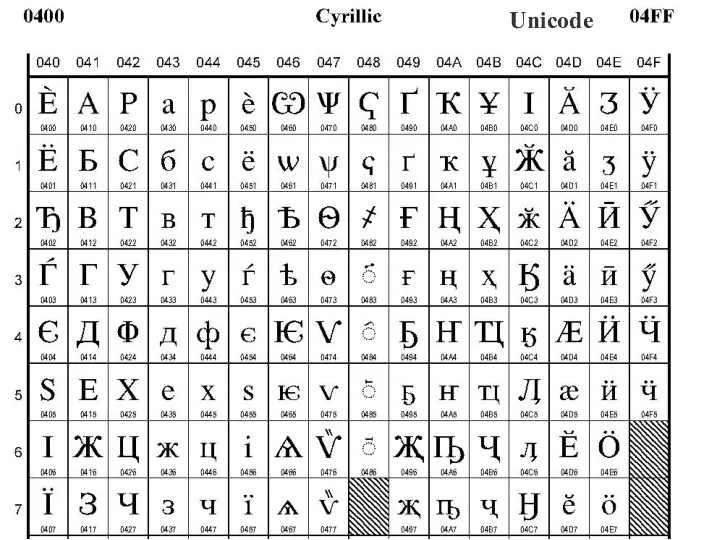
- 10. Unicode
- 11. КОДИРОВАНИЕ ГРАФИЧЕСКИХ ДАННЫХ пиксели (picture element) номер(координаты) точки код цвета(сумма RGB)
- 12. КОДИРОВАНИЕ ЗВУКОВОЙ ИНФОРМАЦИИ Метод FM (Frequency Modulation) Метод таблично-волнового (Wave-Table) синтеза
- 13. СИСТЕМЫ СЧИСЛЕНИЯ непозиционные позиционные
- 14. Кирилли́ческая Непозиционные Системы счисления
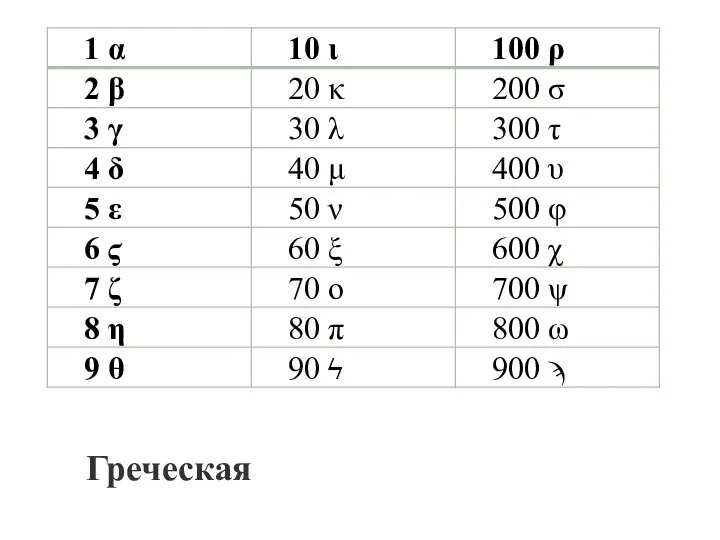
- 15. Греческая
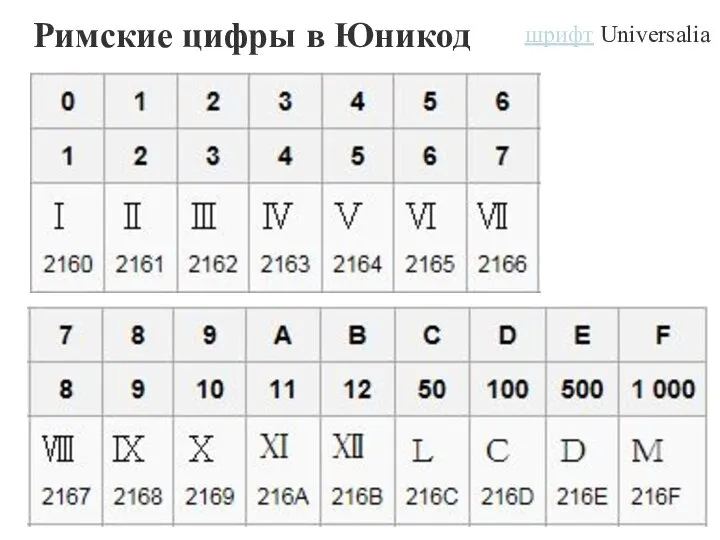
- 16. Римские цифры в Юникод шрифт Universalia
- 18. Позиционные системы счисления А10 = 131 = 100 + 30 + 1 однородные смешанные система измерения
- 19. 307 известных системах счисления только лишь первобытных народов американского континента древнегреческий абак был основан на двоично-пятиричной
- 20. Основные характеристики позиционных систем счисления : основание системы счисления q; значения цифр (символов) ak ; вес
- 21. 1961,56 = 1*103 + 9*102 + 6*101 + 1*100 +5*10-1 + 6*10-2 k – номер разряда
- 23. Двоичная система счисления (q = 210 = 102)
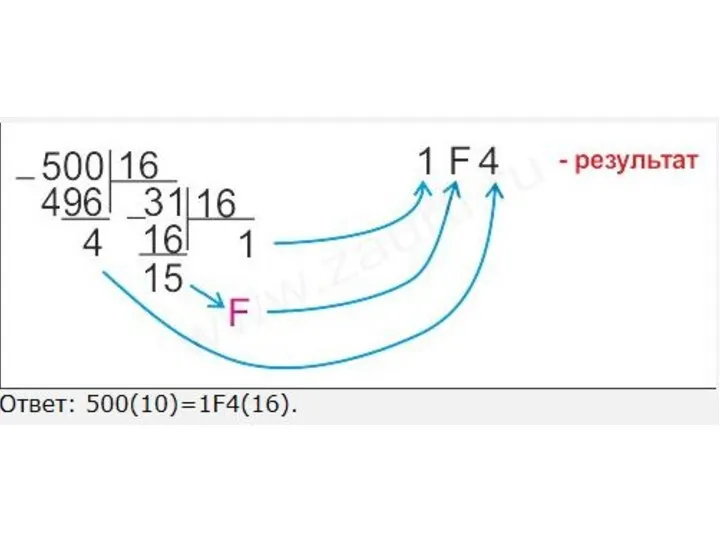
- 24. Шестнадцатеричная система счисления (q = 1610 = 1016) 1010= А16, 1110 = В16, 1210 = С16,
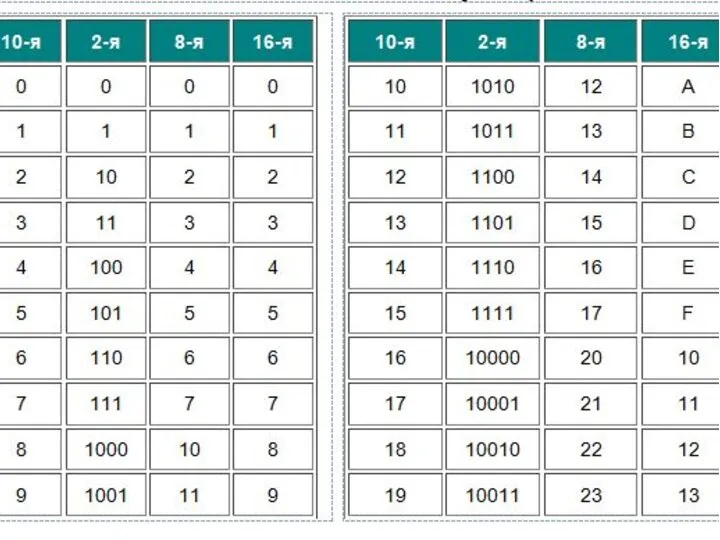
- 26. Способы перевода чисел из одной позиционной системы счисления в другую Табличный метод
- 32. Расчетный метод перевод целых чисел, перевод правильных дробей, перевод неправильных дробей
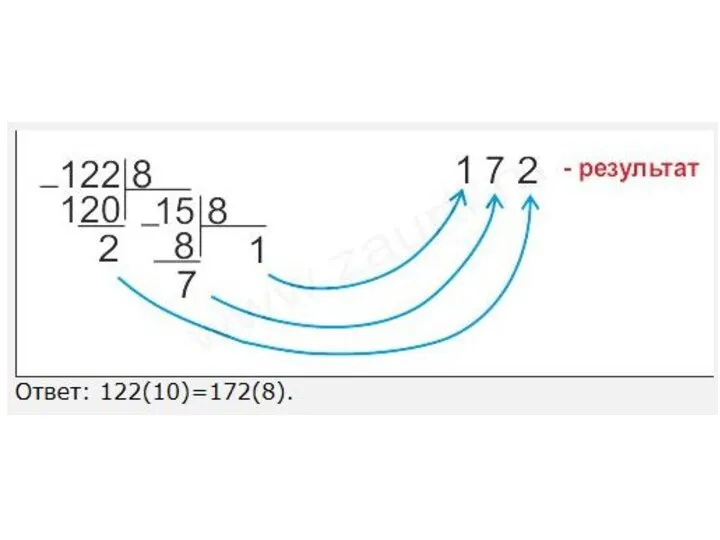
- 33. перевод целых чисел (19)10 = (10011)2
- 34. int dec, bin=0, j; // из десятичного в двоичное cin >> dec; for(j=0; dec>0; j++) {
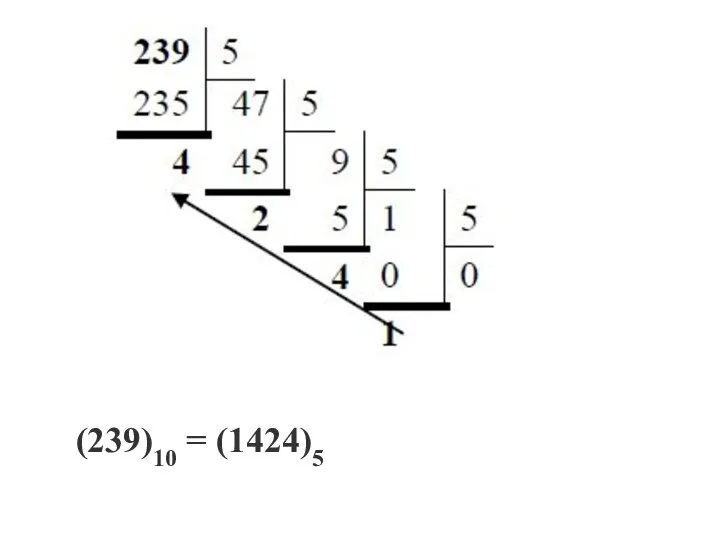
- 35. (239)10 = (1424)5
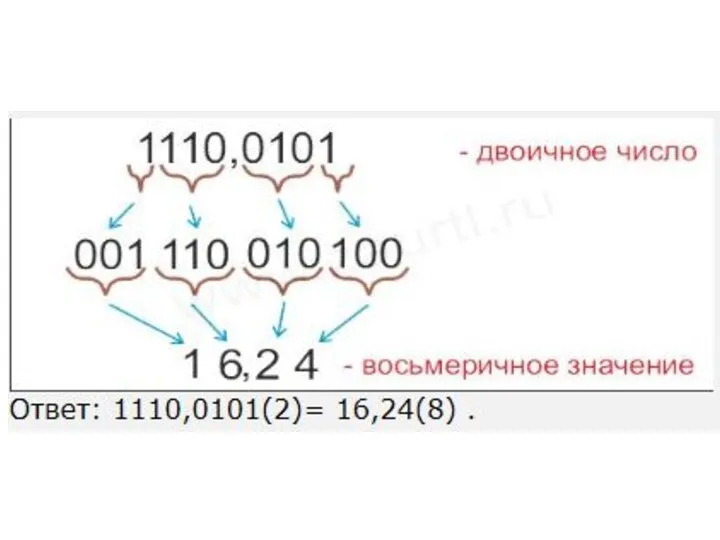
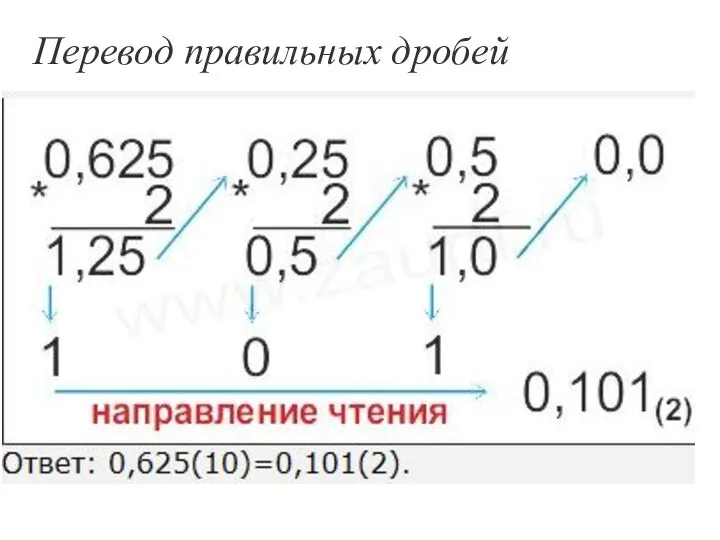
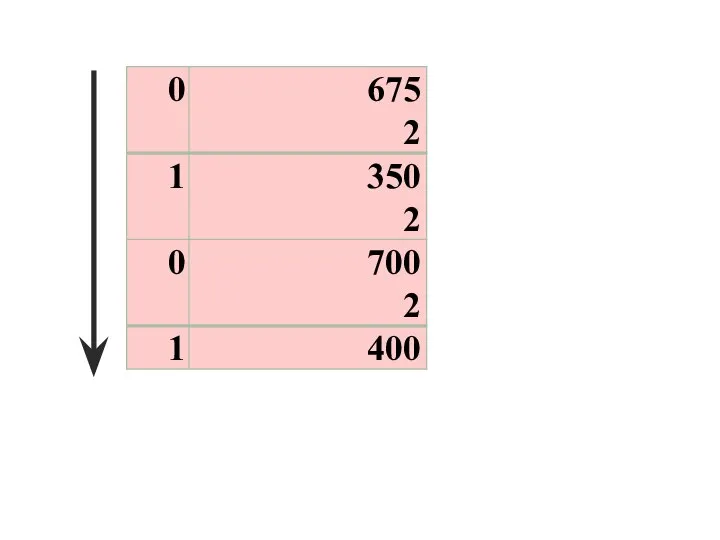
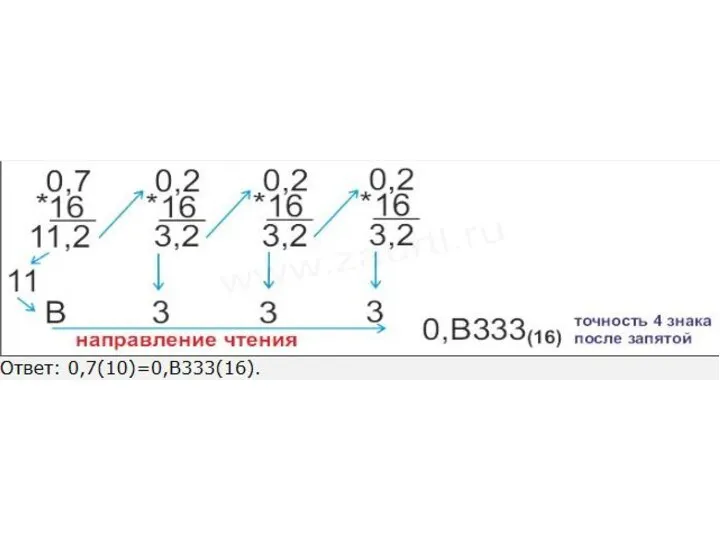
- 38. Перевод правильных дробей
- 42. Перевод неправильных дробей А = 19,67510 = 10011,1012
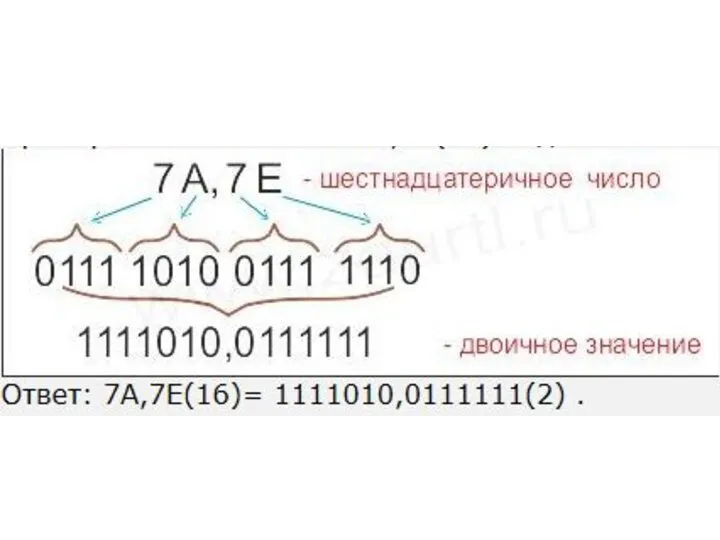
- 43. Перевод из недесятичной системы в десятичную
- 44. //из двоичного в десятичное int var, result = 0; cout cin >> var; for (int r
- 46. ФОРМЫ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ В ЭВМ естественная форма (с фиксированным положением точки) нормальная форма ( с плавающей
- 47. естественная форма +0,10101 -0,10101 m-разрядное число
- 48. .
- 49. нормальная форма где МА – мантисса числа А; q – основание системы счисления; L – порядок
- 51. СПОСОБЫ КОДИРОВАНИЯ ДВОИЧНЫХ ЧИСЕЛ В ЭВМ кодирование знака числа; упрощение операции сложения отрицательных чисел
- 52. специальные машинные коды: прямой; дополнительный; обратный.
- 53. Прямой код Апр = А , если А ≥ 0, 1-А , если А А =
- 54. Обратный код Aобр = А, если А ≥ 0 102 – 10-n+А, если А n –
- 55. Дополнительный код Адоп = А, если А ≥ 0 , 102+А, если А А = +0,1101
- 56. Сложение чисел в дополнительном и обратном кодах
- 58. Скачать презентацию















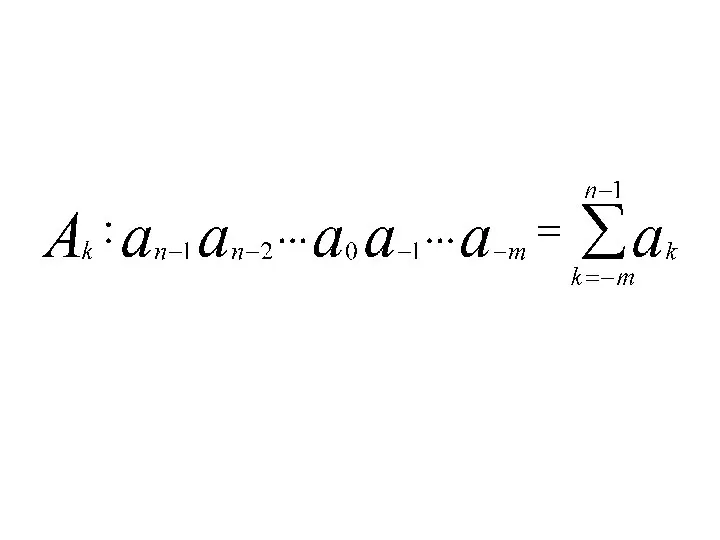
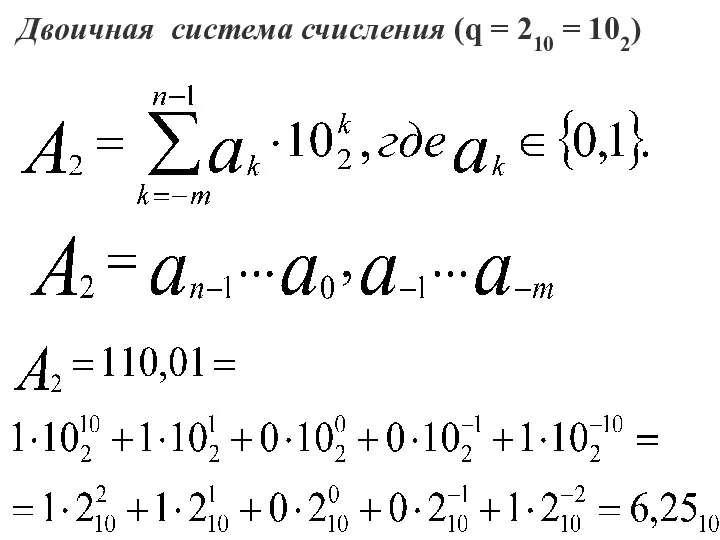

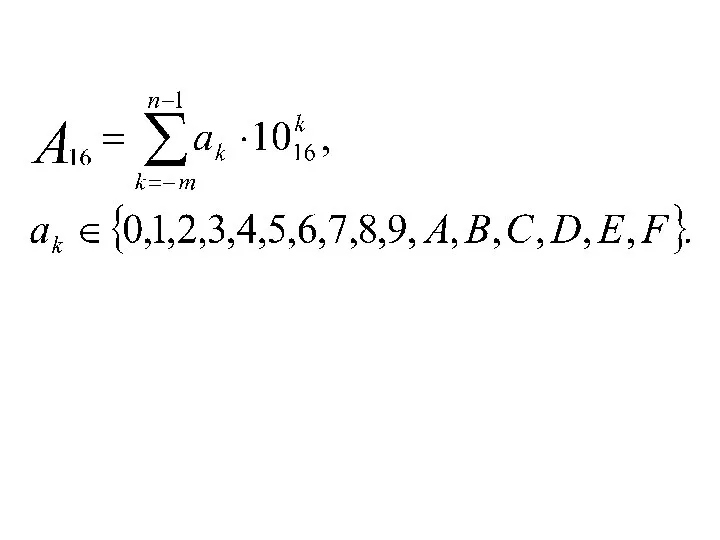













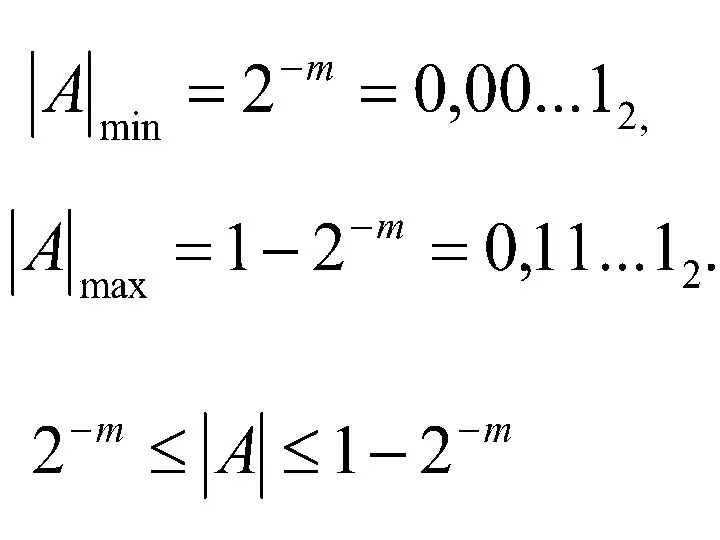

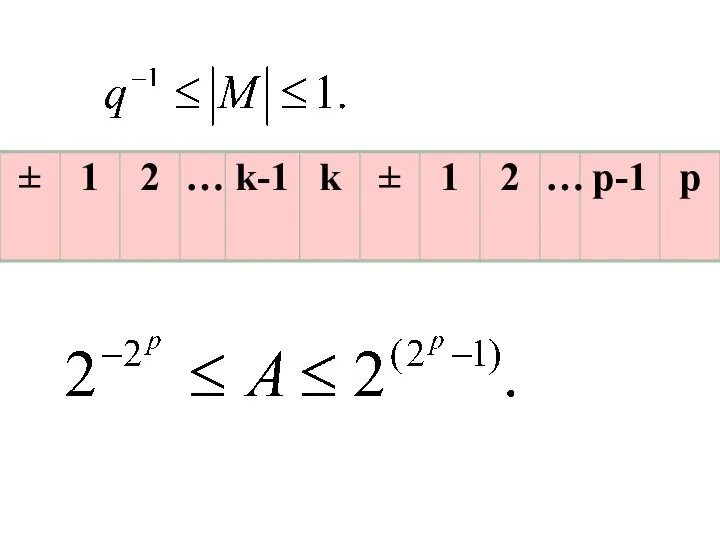


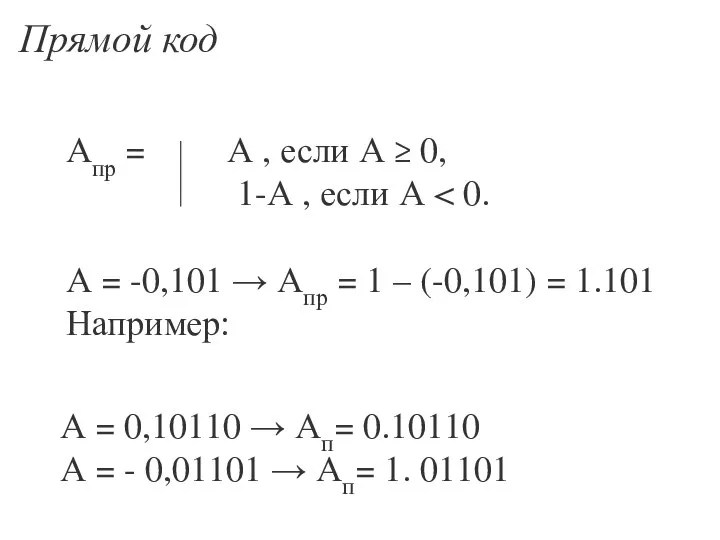



 Сomputer game in the bartender simulator
Сomputer game in the bartender simulator Урок 8. Программное обеспечение(дз)
Урок 8. Программное обеспечение(дз) Информатика 2 класс. Одинаковые цепочки. Разные цепочки
Информатика 2 класс. Одинаковые цепочки. Разные цепочки Устройство компьютера
Устройство компьютера Математические модели
Математические модели Обозрение - один из жанров аналитической журналистики
Обозрение - один из жанров аналитической журналистики Автоматизированная система как объект информационной защиты
Автоматизированная система как объект информационной защиты Преобразования комплексного чертежа. Способ замены плоскостей проекций. Основные метрические задачи. (Лекция 3)
Преобразования комплексного чертежа. Способ замены плоскостей проекций. Основные метрические задачи. (Лекция 3) Средства телекоммуникации
Средства телекоммуникации BMWSTART (1)
BMWSTART (1) Безопасность в сети Интернет
Безопасность в сети Интернет Информация, информационные процессы и информационное общество
Информация, информационные процессы и информационное общество Microsoft Office
Microsoft Office Прототипы. Наследование
Прототипы. Наследование Интернет-проекты коммуникационных и информационных сайтов, посвященных орфанным заболеваниям
Интернет-проекты коммуникационных и информационных сайтов, посвященных орфанным заболеваниям Удоба. Инструкция по созданию интерактивного плаката
Удоба. Инструкция по созданию интерактивного плаката Информация и информационные процессы
Информация и информационные процессы Архитектура персонального компьютера
Архитектура персонального компьютера Основные этапы информатизации общества
Основные этапы информатизации общества Компьютерная графика. Технические средства компьютерной графики. История компьютерной графики Разновидности компьютерной граф
Компьютерная графика. Технические средства компьютерной графики. История компьютерной графики Разновидности компьютерной граф Цветовое решение фильма
Цветовое решение фильма Почта и журналистика
Почта и журналистика SMM специалист с нуля
SMM специалист с нуля Образование в сети
Образование в сети История и современная парадигма информационной безопасности
История и современная парадигма информационной безопасности Склейка карт по фотографиям
Склейка карт по фотографиям ТЗ для лендинга. Фармацевтическая компания Изварино Фарма
ТЗ для лендинга. Фармацевтическая компания Изварино Фарма Аналитика в геймдизайне
Аналитика в геймдизайне