Системы счисления

Система счисления – это способ записи чисел
с помощью заданного набора специальных
знаков (цифр)
значение цифры не зависит от
её позиции в числе
значение каждой цифры изменяется
в зависимости от её положения
Системы счисления
непозиционные позиционные
Единичная Двадцатеричная народов
племени Майя
Римская Вавилонская
(цифры I, V, X, L, C, D, M)
Древнегреческая Двоичная
Славянская Десятичная
кириллическая (0 1 2 3 4 5 6 7 8 9)

Основание системы – это количество
различных знаков, используемых для
изображения чисел в данной системе.
Позиция цифры в числе называется разрядом.
Алфавит двоичной СС: 0, 1.
Алфавит восьмеричной СС : 0, 1, 2, 3, 4, 5, 6, 7
Алфавит шестнадцатеричной СС: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Недостающие цифры заменяются буквами: А, В, С, D, E, F.

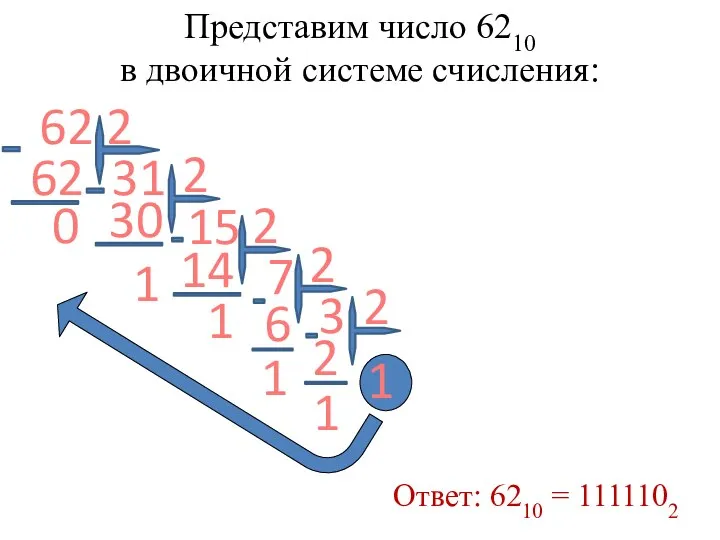
Представим число 6210
в двоичной системе счисления:
31
0
15
7
3
1
Ответ: 6210 = 1111102

Правила перевода
Из десятичной системы счисления
в позиционные системы счисления:
Разделить десятичное число на основание системы счисления. Получится частное и остаток.
Выполнять деление частного до тех пор, пока оно не станет меньшим основания новой системы счисления.
Записать последнее частное и все остатки в обратном порядке. Полученное число и будет записью в новой системы счисления.

Ответ: 1111102=6210
1 1 1 1 102=
5 4 3 2 1 0
1×25+1×24+1×23+1×22+ 1×21 +0×20=
32+16+8+4+2+0=6210
Представим число 1111102
в десятичную систему счисления

Правила перевода
Из позиционной системы счисления
в десятичную систему счисления:
Пронумеруем цифры числа справа налево, начиная с 0 (расставим разряды)
Слева на право складываем произведение каждой цифры числа на основание в степени разряда.
Полученное число и будет записью в десятичной системе счисления.

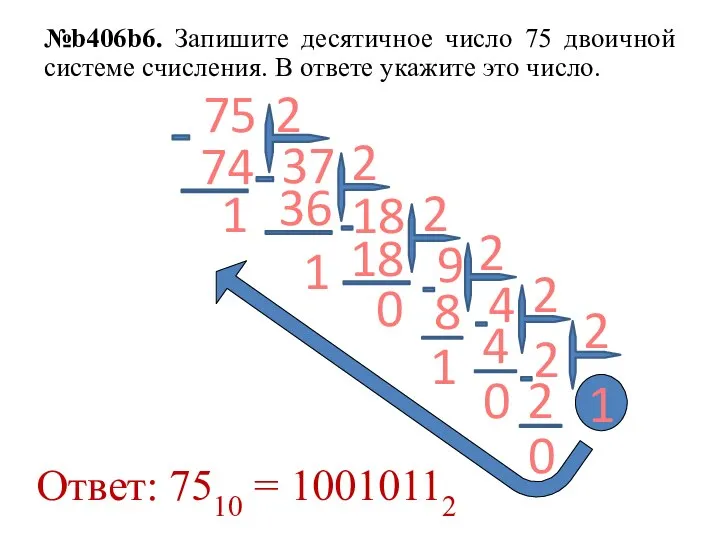
№b406b6. Запишите десятичное число 75 двоичной системе счисления. В ответе укажите это число.
37
1
18
9
4
1
2
Ответ: 7510 = 10010112

№b61af0. Переведите десятичное число 189 в двоичную систему счисления
94
1
47
23
11
5
1
2
Ответ: 18910 = 101111012

№b689f3. Переведите число 139 из десятичной системы счисления в двоичную. Сколько единиц содержит полученное число? В ответе укажите одно число – количество единиц.
69
1
34
17
8
4
1
2
Ответ: 4
13910 = 100010112

Ответ: 117
11101012=
6 5 4 3 2 1 0
1×26+1×25+1×24+0×23+1×22+ 0×21 +1×20=
64+32+16+0+4+0+1=
№F23DAE. Переведите двоичное число 1110101 в десятичную систему счисления.
11710
Ответ: 38
1001102=
5 4 3 2 1 0
1×25+0×24+0×23+1×22+ 1×21 +0×20=
32+0+0+4+2+0=
№E4A102. Некоторое число в двоичной системе счисления записывается как 100110. Запишите это число в десятичной системе.
3810