Слайд 2 1. Задача о кратчайшем пути между двумя вершинами ориентированного графа и

ее экономическая интерпретация.
Слайд 4Экономическое содержание задачи

Слайд 11Сети. Отношение порядка между вершинами ориентированного графа.
Ориентированный граф без циклов, имеющий

одну вершину без входящих дуг (вход графа, источник) и одну вершину без выходящих дуг (выход графа, сток), называется сетью.
Отыскание экстремальных путей на графах такого вида используется в различных экономических расчетах. К их числу относятся рассмотренная выше задача, а также задачи сетевого планирования.
.
Слайд 162. Задача о пути максимальной длины между двумя вершинами ориентированного графа в

сетевом планировании.
Слайд 18о пути максимальной длины
Решение задачи состоит как в отыскании пути максимальной

длины между двумя фиксированными вершинами графа, так и в определении величины этого пути.
Одну из основных задач сетевого планирования составляет отыскание путей максимальной длины между входом и выходом графа-сети.
Слайд 23Сетевое планирование. Скорейшее время завершения проекта.
Рассмотрим проект – совокупность операций

(работ), составляющий некоторый многошаговый процесс. Примером может служить строительство некоторого объекта. Считаем известными все работы, которые предстоит совершить, их последовательность и время, необходимое для выполнения каждой работы.
Проект может быть изображен в виде графа-сети. Зададимся целью определить кратчайший срок завершения проекта.
Слайд 24Пусть данные о строительстве приведены в следующей таблице:

Слайд 25Сетевое планирование
Эту информацию о проекте представим в виде графа-сети. Дугами графа

будем изображать работы, а вершины графа – некоторые события.
Назовем элементарными событиями начало и конец каждой работы, а некоторую совокупность элементарных событий – событием.
Слайд 27Сетевое планирование
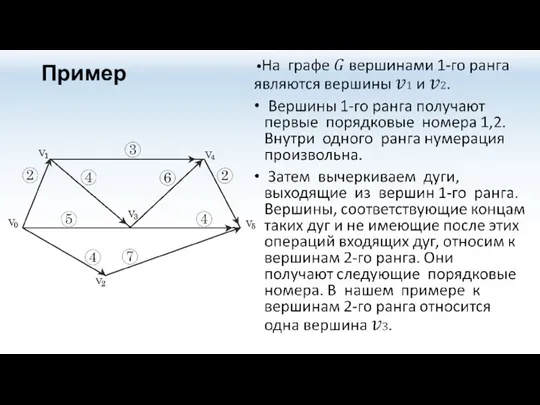
Сетевой граф, соответствующий приведенным в таблице данным, изображен на рисунке.

Номер работы обозначен числом вне кружка. Число, обведенное кружком, есть продолжительность данной работы.




























 Life hacks for medical students
Life hacks for medical students Языки программирования. Pascal
Языки программирования. Pascal Каскадные таблицы стилей
Каскадные таблицы стилей Мультимедийная журналистика
Мультимедийная журналистика Электронные таблицы
Электронные таблицы Молодежная медиасфера
Молодежная медиасфера Из каких частей состоит книга
Из каких частей состоит книга ConnectKey – новые контроллеры для офисных МФУ
ConnectKey – новые контроллеры для офисных МФУ HyperChem HOW to USE
HyperChem HOW to USE Принципы динамического программирования на примере задачи поиска кратчайшего пути на клеточном поле
Принципы динамического программирования на примере задачи поиска кратчайшего пути на клеточном поле Дизайн и графика. Web-страницы
Дизайн и графика. Web-страницы Информация. Введение
Информация. Введение Техническое и информационное обеспечение информационных сиситем
Техническое и информационное обеспечение информационных сиситем 5298
5298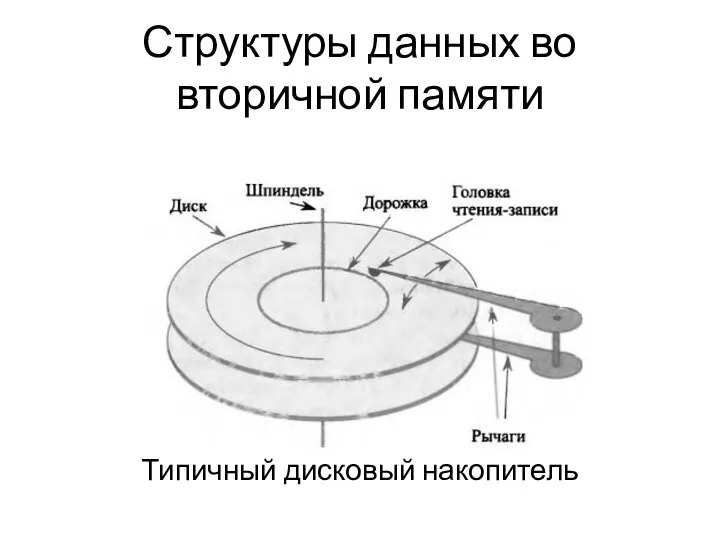 Структуры данных во вторичной памяти
Структуры данных во вторичной памяти Компьютерная графика (7 класс)
Компьютерная графика (7 класс) EW2-week 1
EW2-week 1 Внеклассное мероприятие по информатике «Турнир знатоков компьютера» Учитель информатики МБОУ лицея с. Хлевное Чеканова Н.В.
Внеклассное мероприятие по информатике «Турнир знатоков компьютера» Учитель информатики МБОУ лицея с. Хлевное Чеканова Н.В. Проектирование состава изделия машиностроения с помощью программного обеспечения Лоцман
Проектирование состава изделия машиностроения с помощью программного обеспечения Лоцман Презентация "Информационно-коммуникационные технологии в образовании" - скачать презентации по Информатике
Презентация "Информационно-коммуникационные технологии в образовании" - скачать презентации по Информатике Управление портами микроконтроллера в режиме GPIO
Управление портами микроконтроллера в режиме GPIO Типы алгоритмов
Типы алгоритмов IComparable
IComparable Стиллер
Стиллер Материнская плата
Материнская плата Медиастрана
Медиастрана Графические форматы и программная реализация базовых алгоритмов компьютерной графики
Графические форматы и программная реализация базовых алгоритмов компьютерной графики Тест для выпускников 2021. Фотография
Тест для выпускников 2021. Фотография